思路突破探考题，反思微设觅方法

赵平

[摘  要] 圆锥曲线是高考的热点内容，常作为压轴题出现. 优秀的高考真题是众多命题专家智慧的结晶，通过探究真题不仅可以获得考题的命题思路、知识重点，还可以从中提取宝贵的方法和经验，提升数学思维. 因此对于优秀的考题，需要透过表象，深入探究本质，拓展解题思维. 2020年江苏高考数学第18题的命题视角、解法思路具有极高的研究价值，文章将对其探究解读，教学反思.

[关键词] 圆锥曲线;几何;向量;面积;模型

■真题呈现，思路突破

1. 真题呈现

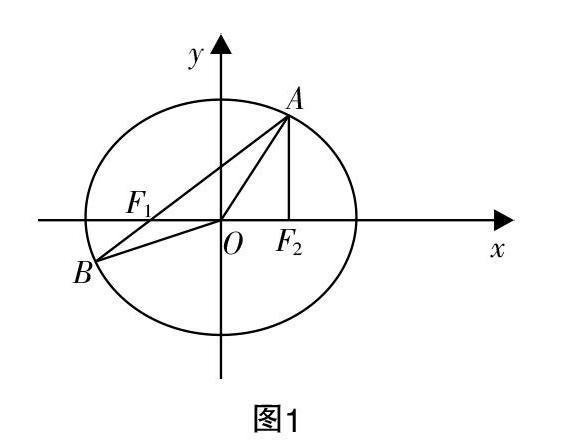
考题（2020年江苏高考数学卷第18题）：在平面直角坐标系xOy中，已知椭圆E：■+■=1的左、右焦点分别为F■，F■，点A在椭圆E上且在第一象限内，AF■⊥F■F■，直线AF■与椭圆E相交于另一点B.

（1）求△AF■F■的周长;

（2）在x轴上任取一点P，直线AP与椭圆E的右准线相交于点Q，求■·■的最小值;

（3）设点M在椭圆E上，记△OAB与△MAB的面积分别为S■，S■，若S■=3S■，求点M的坐标.

2. 思路突破

上述是以椭圆为基础，融合三角形、向量积的圆锥曲线综合题，主要考查椭圆的定义，圆锥曲线中几何周长、面积的处理方法，向量积的转化思路，等等. 问题突破需要立足基础知识——以基本的定理、定义为基础，合理选用方法转化求解.

（1）该问依托椭圆的焦点构建了△AF■F■，由椭圆方程可知长半轴a=2，短半轴b=■，半焦距c=1，由椭圆的定义可知AF■+AF■=2a=4，所以△AF■F■的周长为2a+2c=6.

（2）该问设定x轴上一点P，联系原点O和椭圆构建了向量■和■，求向量积■·■的最小值可以采用“设点→坐标转化→最值分析”的思路. 首先设定点P（x■，0），求出点A的坐标，表示点Q的坐标;然后由向量积的坐标公式建立关于点P坐标参数的二次函数式，利用函数的性质完成求解.

设点P（x■，0），由题意可知x■≠1，由于点A在椭圆E上，且位于第一象限，结合AF■⊥F■F■可求得点A的坐标为1，■. 又知椭圆E的准线方程为x=4，所以点Q可设为（4，y■），则■·■=（x■，0）·（x■-4，-y■）=（x■-2）2-4≥-4，即■·■的最小值為-4.

（3）该问设定椭圆E上一点M，构建了△OAB与△MAB，求解面积关系为S■=3S■时点M的坐标，属于圆锥曲线中的几何面积问题. 解析时需要设出点M的坐标，构建相应的面积模型，利用面积关系可转化出与点M的坐标相关的条件，进而联立椭圆方程可解得点M的坐标.

设点M的坐标为（x■，y■），点M到直线AB的距离设为d. △OAB与△MAB可视为是以AB为底，分别以点O和点M为顶点的三角形，则三角形的面积可表示为S■=■·AB·d■（d■表示点O到直线AB的距离），S■=■·AB·d. 已知点A1，■，F■（-1，0），则直线AF■的方程为y=■（x+1），由点到直线的距离公式可知d■=■. 已知S■=3S■，所以3×■×AB×■=■·AB·d，所以d=■，所以3x■-4y■+3=9①. 又知点M的坐标满足方程■+■=1②，联立方程①②可得3x■-4y■+3=9，■+■=1，解得x■=2，y■=0，或x■=-■，y■=-■.检查均满足条件，所以点M的坐标为（2，0）或-■，-■.

■解后反思，教学微设

上述是高考常见的圆锥曲线综合题，涉及椭圆、三角形、向量等知识，对学生的数学思维和运算技巧有着较高的要求. 引导学生体验思路突破是考题教学第一步，而第二步的解后反思、教学微设计同样十分重要，可深度挖掘考题，总结方法，形成同类型问题的解题策略.

1. 问题突破的关键

本考题的综合性极强，所设三小问具有鲜明的特点，需透过问题表象，挖掘本质. 第一问求解△AF■F■的周长，由于焦距已知，实际上就是求动点A到两焦点距离之和，显然突破的关键是利用椭圆的定义. 第二问属于向量积的最值问题，显然需要将向量问题转化为相应的函数问题，故突破的关键是利用向量积的坐标运算来灵活转化. 第三问属于动点几何面积问题，需要从面积关系中提取线段条件，进而推理点的坐标，故实际突破的关键点有两个：一是基于面积公式建立同底三角形模型，二是利用点到直线的距离公式转化出线段关系. 考题后两问的计算量相对较大，解析时需要灵活运用公式，降低计算量.

2. 解法借鉴之处

学习圆锥曲线考题的解法是关键，反思考题需要充分挖掘其中的解法价值. 如第一问求三角形的周长，需要学习椭圆定义法;第二问求向量积的最值，则需要学习其中的设点法、向量积的坐标处理方法，以及利用函数的性质研究最值的策略;第三问求三角形面积的方法综合性强，但核心解法为模型转化法、利用点到直线的距离公式求解线段之长. 考题的后两问可视为动点问题，合理设定动点、不确定点的坐标极为重要，但在实际求解时需要灵活运用韦达定理、“设而不求”的思想来简化运算.

3. 考题的教学微设计

开展考题教学微设计可以帮助学生全面认识考题结构，由浅入深地呈现解法，贯通解题思路，教学中可分如下三步进行设计.

第一步，题干呈现，热身练习.

例1：在平面直角坐标系xOy中，已知椭圆E：■+■=1的左、右焦点分别为F■，F■.

（1）试求椭圆的长半轴a、短半轴b和半焦距c的值，以及焦点F■，F■的坐标;

（2）点A是椭圆位于第一象限的一点，利用椭圆的定义求AF■+AF■的值，并推导△AF■F■的周长.

教学引导：引导学生回顾椭圆的特征方程和定义，求解椭圆方程的相关参数，进行基础强化，知识巩固.

第二步，深入探究，求解向量最值.