由“1千克的水能浮起1千克的木块吗？”引发的思考

郝志奇

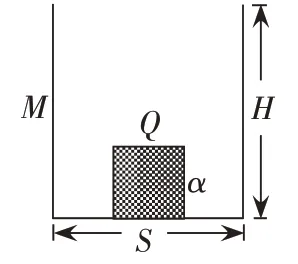
1千克的水能浮起1千克的木块吗？为了解决上述问题，我们先从一道中考模拟题说起。如图，一个圆柱形平底容器，底面积为5×10-2m2，把它放在水平桌面上，在容器内放入一个底面积为2×10-2m2，高为0.15m的圆柱形物块，且与容器底不完全密合，物块的平均密度为0.8×103kg/m3(g取10N/kg)，容器内缓慢注水，使物块对容器底的压强恰好为零时，向容器内注入水的质量是( )。

A.2.4kg B.3.6kg C.12kg D.24kg

我们很容易解得答案是B。

过程如下：由题意知：F浮=G物，则ρ水gV排=ρ物S物H物g

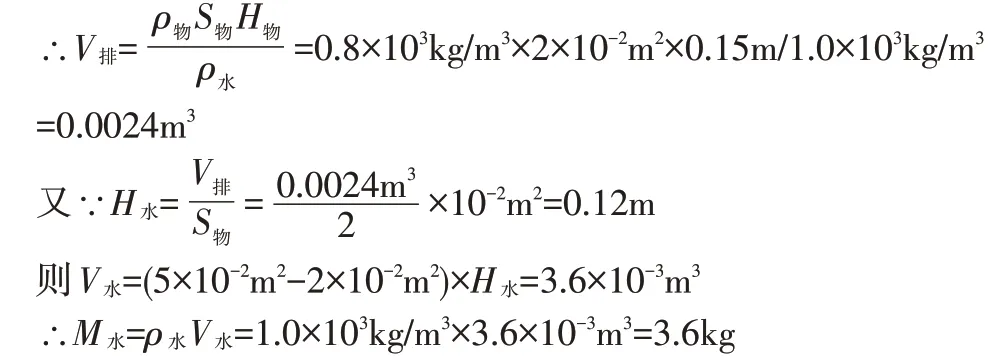
我们可以从以下思路做如下思考：假设圆柱体的底面积为S1，圆柱形平地容器底面积为S2，圆柱体恰好被水浮起(即它对容器底的压强恰好为零)时，容器中水的深度为H水，圆柱体的平均密度为ρ物，圆柱体的高为H物，圆柱体的质量为M物。

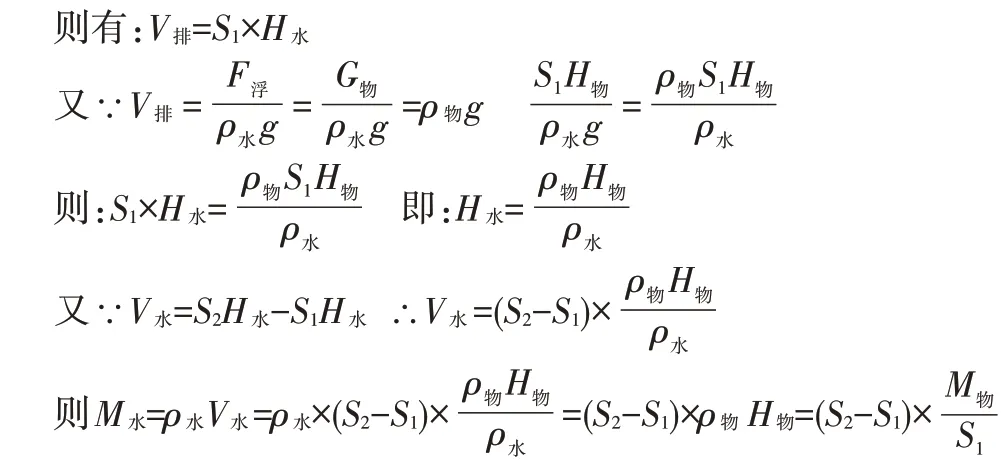
讨论：在ρ物-ρ水，F压=0的条件下：

当S2=S1时：M水=0 当S2=2S1时：M水=M物

当2S1＞S2＞S1时：M水-M物当S2=ns1时：M水=(n-1)M物

可见：圆柱体恰好被水浮起，圆柱形容器中所注入水的质量与圆柱体物块的底面积、圆柱形容器的底面积以及圆柱体物块的质量(或圆柱体物块的重量)有关。不难看出在一定条件下1千克的水完全可以浮起1千克的木块。

则上题中可将计算过程简化为：

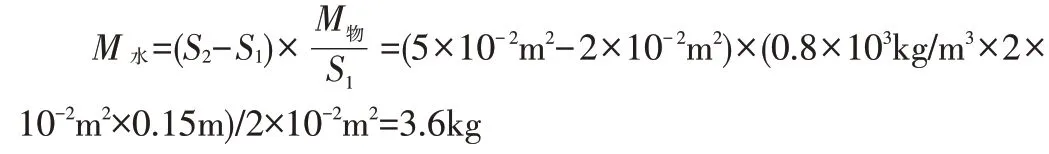
原理应用：例1：如图圆柱形平底容器，底面积为500cm2，其中盛有水，水的深度为8cm，现将一质量为1.8kg，底面积为100cm2的长方体木块放入容器中，液面上升了2cm，如图所示。

求：1.木块对容器底的压强。

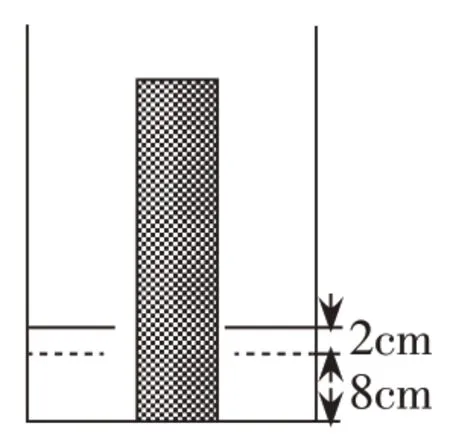
2.缓慢向容器中注入水，至少再加多少千克水，才能使木块对容器底的压强为零(g取10N/kg)？

此题虽然很简单，但设计问题与上述物理模型基本相同，所以完全可以做到同发炮制，快速求解。

分析与解：本题初看较上题繁杂，实际上则大同小异，如出一辙。因为它们的目标相同，即都是让物块对容器底的压强恰好为0(第一问从略)。设当木块对容器底的压强为0时容器中总共注入水的质量为M水，则M水=(500cm2-100cm2)×1.8kg/100cm2=7.2kg

∴容器中至少再加的水Δm水=M水-M1水=M水-1.0×103kg/m3×500cm2×8cm=7.2kg-4.0kg=3.2kg

例2：圆柱形容器中盛有水。现将一质量为0.8千克的正方体物块放入容器中，液面上升了1厘米。此时正方体物块有一半露出水面。已知容器的横截面积与正方体横截面积之比为5∶1(g取10牛/千克)，容器壁厚不计。求：1.物块对容器底的压强；2.若再缓缓向容器中注入水，至少需要加多少水，才能使物块对容器底的压强为零。

分析与解：设正方体物块边长为a，则其面积为s1=a2，圆柱形容器底面积就为S2=5a2

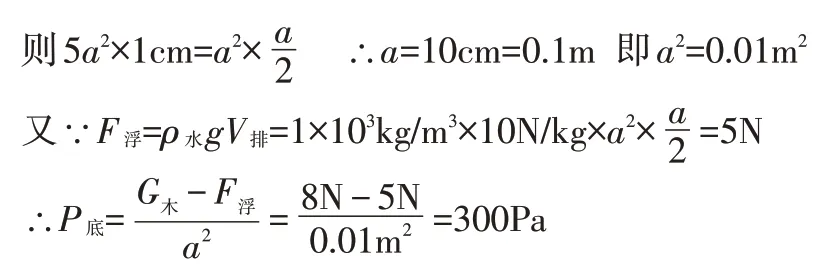
(2)设容器中总共注入水的质量为M水：则M水=(s2-a2)×0.8千克/a2

例3：如图所示，一容器M底面积为S，高为H，其内放一立方体木块Q，边长为a，重为G1，向容器内倒入重为G的水后，木块对容器底的压力恰好为零，则容器内水的深度为( )