汽缸类问题的几种常见类型

裴承仁

汽缸问题的常见类型有以下三种。

一、气体系统处于力学平衡状态，需综合应用气体实验定律和物体的平衡条件解题

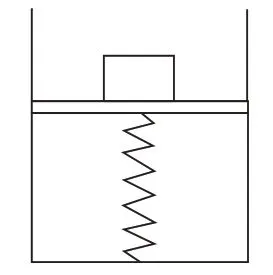
例1.在一个横截面积为S=10cm2的圆柱形容器中，有一个质量不计的活塞用弹簧和底部相连，容器中密闭有一定质量的理想气体，当温度为t1=27°C时，弹簧恰好处于原长，此时外部压强为p0=1.0×105Pa，活塞和底面相距L=20cm，在活塞上放一质量为m1=20kg的物体，活塞静止时下降10cm，温度仍为27℃，不计活塞与容器壁的摩擦，弹簧的形变在弹性限度范围内，g=10m/s2，求：

(1)弹簧的劲度系数k。

(2)如果把活塞内气体加热到t2=57℃并保持不变，为使活塞静止时位置距容器底面距离仍为10cm，活塞上应再加物体的质量m2。

解析：(1)对封闭气体，由玻意耳定律得：p0LS=p1hS

以活塞与重物组成的系统为研究对象，由平衡条件得：m1g+p0S=p1S+kx

解得k=1000N/m。

(2)升高温度的过程中气体的体积保持不变，设温度升高后的压强为p2，则：

T1=273+t1T2=273+t2

要活塞仍然保持静止，则：m2g+m1g+p0S=p2S+kx

联立解得m2=2kg。

二、气体系统处于力学非平衡态，需综合应用气体实验定律和牛顿运动定律解题

例2.如图所示，一汽缸水平固定在静止的小车上，一质量为m、面积为S的活塞将一定量的气体封闭在汽缸内，平衡时活塞与汽缸底相距L。现让小车以一较小的水平恒定加速度向右运动，稳定时发现活塞相对于汽缸移动了距离d，已知大气压强为p0，不计汽缸和活塞间的摩擦；且小车运动时，大气对活塞的压强仍可视为p0，整个过程温度保持不变，求小车加速度的大小。

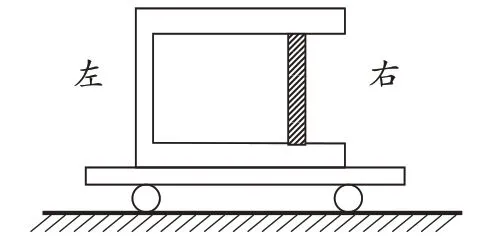
解析：设小车加速度大小为a，稳定时汽缸内气体的压强为p1，则：

活塞受到汽缸内、外气体的压力分别为：F1=p1S,F0=p0S，

由牛顿第二定律得F1-F0=ma，

小车静止时，在平衡情况下，汽缸内气体的压强应为p0，由玻意耳定律得p1V1=p0V0，式中V0=SL，V1=S(L-d)

三、对于两个或多个汽缸封闭着几部分气体，并且汽缸之间相互关联的问题，解答时不仅要分别研究各部分气体，找出它们各自遵循的规律，并写出相应的方程，还要写出各部分气体之间压强或体积的关系式，最后联立求解

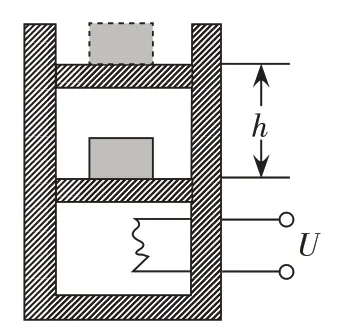
例3.如图所示，将一个绝热的汽缸竖直放置在水平桌面上，在汽缸内用一个活塞封闭了一定质量的气体。在活塞上面放置一个物体，活塞和物体的总质量为10kg，活塞的横截面积为：S=100cm2。已知外界的大气压强为P0=1×105Pa，不计活塞和汽缸之间的摩擦力。在汽缸内部有一个电阻丝，电阻丝的电阻值R=4Ω，电源的电压为12V。接通电源10s后活塞缓慢升高h=10cm，求这一过程中气体的内能变化量。若缸内气体的初始温度为27℃，体积为3×10-3m3，试求接通电源10s后缸内气体的温度是多少？

解析：设汽缸内气体的压强为p，选活塞为研究对象，活塞缓慢移动受力平衡，根据力的平衡知识得：

活塞在上升h=10cm的过程中气体对外界做功W=Fh=pSh=110J。

因为汽缸是绝热的，所以电阻丝产生的热量全部被气体吸收。

根据热力学第一定律得：ΔU=-W+Q=250J,即气体的内能增加了250J。

汽缸类问题是高考中的常见题型，对于以上常见的三种类型，一般的解题思路为：1.确定研究对象。一般研究对象分为两类：一类是热学研究对象(一定质量的理想气体)；另一类是力学研究对象(汽缸、活塞或某系统)。2.分析清楚题目所述的物理过程，对热学研究对象分析清楚初、末状态及状态变化过程，依据气体实验定律列出方程；对力学研究对象要正确地进行受力分析，依据力学规律列出方程。3.挖掘题目中的隐含条件，如几何关系等，列出辅助方程。4.多个方程联立求解。对求解的结果注意分析它们的合理性。