函数知识引领与题型点击

孟宪玲

一、以三次函数为主线的问题

三次函数交汇了不等式、方程、解析几何等众多知识点，以它为载体的试题背景新颖、独特，选拔功能强。由于三次函数的导数为二次函数，因此以导数为工具，可用二次函数知识对三次函数的形态进行研究。

例1：已知f(x)=x3+ax2+bx+c在与x=1时都取得极值。

1.求a，b的值；

2.若对x∈[-1，2]，f(x)＜c2恒成立，求c的取值范围。

思路分析：因为函数在与x=1时都取得极值，所以其导数值为0，可求得

因f(2)=2+c＞。

所以当x∈[-1，2]，f(x)的最大值为f(2)=2+c。

因为x∈[-1，2]，f(x)＜c2恒成立，

所以c2＞2+c，c＜-1，或者c＞2故c的取值范围为(-∞，-1)∪(2，+∞)。

友情提醒：

(1)考查三次函数的单调性、极值与最值等问题，要通过对三次函数的求导，可将“三次”变为“二次”，于是转化为考查熟悉的二次函数、二次方程及相关问题。

(2)对于恒成立问题，例如x∈[-1，2]，f(x)＜c2恒成立，总有：

x∈[-1，2]，f(x)的最大值＜c2，因而问题转化为求x∈[-1，2]，f(x)的最大值。

例2：求过点P(0，0)且与曲线相切的切线方程。

思路分析：因为点P(0，0)在曲线上，它可以是切点，也可能不是切点。当点P(0，0)是切点时，由k=f′(0)=4，求得切线方程为y=4x，当点P(0，0)不是切点时，另设切点Q(x0，y0)，(x0≠0)，则以Q为切点的切线的斜率为k1=-2x0+2x0+4，又，解得，得切线方程为。故过点P（0，0）且与曲线相切的切线方程有两条，其方程为y=4x和此时，一个切点是P(0，0)，另一个切点是

友情提醒：

1.求过一点P(x0，y0)的曲线y=f(x)的切线方程与求过曲线y=f(x)上一点P(x0，y0)的切线方程，虽然是同一类问题，但有所不同。前者曲线的切线其切点可以是P(x0，y0)，也可以是曲线上其余的点；切线可以存在，也可不存在。若存在，切线可以不唯一。而后者一般情况下，点P(x0，y0)是曲线的切点，以P(x0，y0)为切点的切线是唯一存在的。

2.曲线与直线相切，并不一定只有一个公共点，当曲线是二次曲线时，直线和曲线相切，有且只有一个公共点。这种观点对一般的曲线不一定正确，上例正说明了这一点。

拓展引申：(1)已知抛物线C1∶y=x2+2x和抛物线C2∶y=-x2+a，当a取什么值时，C1，C2有且仅有一条公切线？写出公切线l的方程。

解析：设公切线L切于C1于点P1(x1，y1)，切C2于点P2(x2，y2)，则L的方程有两种表达方式①②分别是

所以P1，P2重合，故当时，C1，C2有且仅有一条公切线，其方程为。

(2)已知函数①若函数f(x)=x3-x2+bx+c的图像有与x轴平行的切线，求b的取值范围；②若f(x)在x=1时取得极值，且x∈[-1，2]时，f(x)＜c2恒成立，求c的取值范围；

解析：①f′(x)=3x2-x+b，设切点P(x0，y0)，则f(x)在点P的切线的斜率k=f′(0)=3x0-x0+b，由题意，k=f′(0)=3x0-x0+b=0有解，故有Δ=1-12b≥0，∴b≤12。

②因为f(x)在x=1时取得极值，所以x=1为方程f ′(x)=3x2-x+b=0的一个根，

∴b=-2由3x2-x-2=0可得f′(x)=0的另一个根当x＜或x＞1，f′(x)＞0，

所以当x∈[-1，2]，时，f(x)在上是增函数，

所以f(x)有极大值

所以当x∈[-1，2]时f(x)有最大值f(2)=2+c，

因为f(x)＜c2恒成立，

∴2+c＜c2恒成立，c＜-1或c＞2。

反思：本题第(1)题利用了导数的几何意义将问题转化为二次方程有解问题。第(2)题为恒成立问题，实质是求函数f(x)在区间[-1，2]上的最大值。

二、以抽象函数为主线的问题

这里所谓的抽象函数，是指只给出函数的一些性质，而未给出函数解析式的一类函数。抽象函数一般以中学阶段所学的基本函数为背景，且构思新颖、条件隐蔽、技巧性强、解法灵活。因此抽象函数在近几年的各种考试中，成为考查的重点。

例3：定义在(-1，1)上的函数f(x)满足：

(1)对任意的x，y∈(-1，1)，都有

(2)当x∈(-1，0)，时，有f(x)＞0，

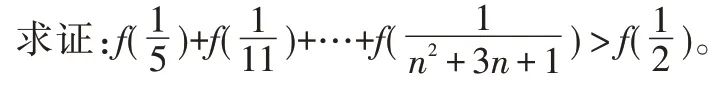
思路分析：先赋值判断奇偶性，令x=y=0，得f(0)=0，再令y=-x，得f(x)+f(-x)=0，所以f(x)是奇函数。再利用定义证明f(x)在x∈(-1，0)时是减函数，则在x∈(0，1)上仍然是减函数，且f(x)＜0。最后将裂项为，于是。

友情提醒：

(1)本题先确定函数的奇偶性和单调性，利用裂项求和进行化简，再根据条件用放缩法证明不等式；在解题过程中，利用题设充分挖掘隐含条件，开拓解题思路，使问题得到解决。

(2)解决抽象函数问题的关键是挖掘函数的特征，考虑特殊值的代入、类比、推理等方法，或脱去抽象函数中的记号f，化为具体函数解决。

拓展引申：

1.设a是常数，函数f(x)对一切x∈R都满足f(a-x)=-f(a+x)。

求证：函数f(x)的图像关于点(a，0)成中心对称图形。

解析：证明一个函数图像的对称性问题，只需在此函数图像上任取一点P，证明它的对称点Q也在其图像上。

证明：∵f(a-x)=-f(a+x)对一切x∈R都成立，

∴f(x)=f[a-(a-x)]=-f[a+(a-x)]=-f(2a-x)]，所以在f(x)的图像上任取一点(x0，y0)，则其关于(a，0)的对称点(2a-x0，-y0)也在其图像上，所以函数f(x)的图像关于点(a，0)成中心对称图形。

2.已知函数f(x)对于一切实数x满足f(x)=f(12-x)，若方程f(x)=0有n个不同的实数根，这n个实数根的和是48，求n的值。

解析：由方程根的意义及等式f(x)=f(12-x)的意义知，方程的根是成对出现的，且成对两根之和是12。

由方程f(x)=f(12-x)知，如果x0是方程的根，那么12-x0也是方程的根，且x0≠12-x0，x0+(12-x0)=12，由48=12×4，可知方程f(x)=0有四对不同的实数根，即方程f(x)=0有8个不同的实根。所以n=8。

三、以向量知识为背景的函数问题

向量由于具有几何形式和代数形式的双重身份，能容数形于一体，因此以向量的相关知识为载体，以数形转化思想方法为主线的函数问题，其设计创新力度较大、综合性较强，已成为近年高考的新热点。

例4：(2005年湖北高考题)已知向量若函数在区间(-1，1)上是增函数，求t的取值范围。

思路分析：

先求出f(x)=x2(1-x)+t(x+1)=-x3+x2+tx+t，则f′(x)=-3x2+2x+t，因为函数f(x)在区间(-1，1)上是增函数，则在(-1，1)上f′(x)≥0，则t≥3x2-2x在区间(-1，1)上恒成立。

考虑函数g(x)=3x2-2x在(-1，1)的取值范围，有g(x)＜g(-1)，于是t≥g(-1)=5。

当t≥5时，函数f(x)在区间(-1，1)上满足f′(x)＞0，即函数f(x)在区间(-1，1)上是增函数，故t≥5。

友情提醒：

1.本题考查平面向量数量积的计算方法，利用导数研究函数的单调性，并运用函数性质分析和解决问题。

2.研究近几年高考试题，发现平面向量与函数知识交汇融合的创新潜力较大，已渐成高考的热点。

拓展引申：

(1)求函数关系式s=f(t)；

(2)若函数s=f(t)在[1，+∞）上是单调函数，求k的取值范围。

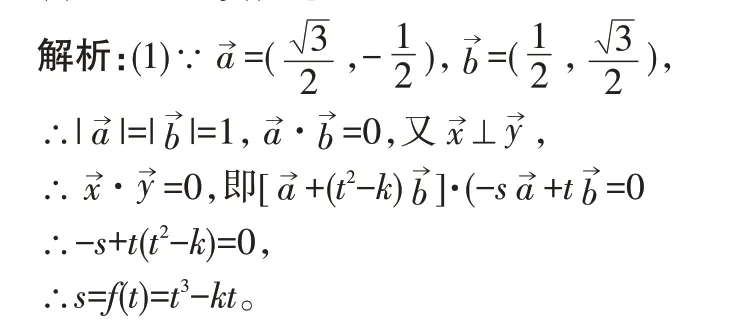
(2)f′(t)=2t2-k，∵f(t)在[1，+∞)上是单调函数，所以在[1，+∞)上有f′(t)≥0，或f′(t)≤0。由f′(t)≥0，可得，k≤3t2，∴k≤(3t2)min，k≤3。由f ′(t)≤0可得k≥3t2，而y=3t2在[1，+∞)上是增函数，没有最大值。此时，不存在k使k≥3t2在[1，+∞)上恒成立。故k的取值范围是k≥3。

四、信息迁移中的函数问题

数学信息题一般取材较新，多以社会热点或最新科技动态为背景，具有浓郁的时代特征和生活气息。在题目中给出的是新情景、新结构、新概念、新函数、新运算等信息，要求学生在考试时完成现场学习，在短时间内从大量的信息中捕捉相关信息，通过分析、归纳，探索有关规律，应用联想、猜想、演绎、类比、迁移等方法将它与已有的知识结合起来，把所学的知识迁移到新的情景中，去做进一步推理、运算、证明，才能获得解决。

例5：设y=f(x)是定义在R上的偶函数，又是最小正周期为π的周期函数，而且f(x)在(0，)上是增函数，试写出函数f(x)的解析式。

思路分析：

这是结论开放型信息迁移题，由于f(x)是周期函数，故容易想到从三角函数入手进行探究。

友情提醒：

1.此类问题读懂题意是关键的一步。搞清题意才能确定探索方向，寻找合理的解题途径。

2.我们常见的是已知f(x)的解析式来分析f(x)，即使是求解析式也往往是已知图像或者函数的一部分解析式，这样的解答结果是唯一确定的；而本问题却是反其道而行之，给出函数奇偶性、单调性和周期性性质，反过来写出符合条件的函数，将信息逆向迁移，具有开放性。