二维正态总体样本相关系数的极限分布

李 琼，武 东

二维正态分布在数学、物理与工程等领域具有十分重要的概率分布，由于该分布函数具有很多很好的性质，在诸多涉及统计科学、离散科学等领域都有重要的影响力.例如图像处理中的Gaussian滤波器；医学中的同质群体的红细胞数与血红蛋白量，成年男子的身高与体重，经济学中的总消费与总支出.相关系数是反映变量之间相关程度的一种度量，在一定程度上反映了变量之间的相互关系.获得样本相关系数的性质在实际中十分重要.赵志文等［1]利用多元函数的中心极限定理推断了二维正态总体的样本相关系数具有渐近正态性并获得了其渐近分布.宋立新［2]和叶萌等［3]在样本相关系数具有渐近正态性的前提下给出了二维正态总体相关系数的假设检验方法.文献［4]研究了二维正态分布样本Gini相关系数的均值和方差的渐近性.文献［5]研究了正态总体情况下次序统计量相关系数的渐近性质.文献［6]研究了一些非正态总体情况下相关系数的统计推断.但上述情况都未讨论二维正态总体部分参数已知情况下样本相关系数的渐近性.鉴于此，本文讨论了正态总体参数已知和未知情况下，二维正态总体样本相关系数的渐近正态性，当样本容量很大时为使用二维正态总体样本相关系数进行假设检验与区间估计提供了理论依据和方法.

1 预备引理

引理1［7]若随机向量(X1,X2,…,Xp)T服从p维正态分布Np(μ,Σ)，这里μ=(μ1,…,μp)T，Σ=(σij)，则关于均值的四阶矩为

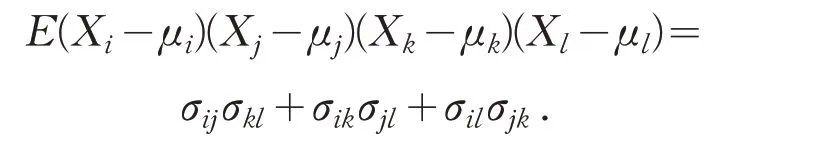
引理2［7-8]令U是具有m阶矩的随机向量序列，b为常数向量，并满足N(0,Σ)，n→∞.令f(u)是向量u的向量值函数且fj(u) 在u=b有非零微分，并令是Φb的第(i,j)个元素，则有极限分布

2 主要结果

定理1［9]设总体(X,Y)T服从二维正态分布N(0,0,1,1,ρ)，其概率密度为

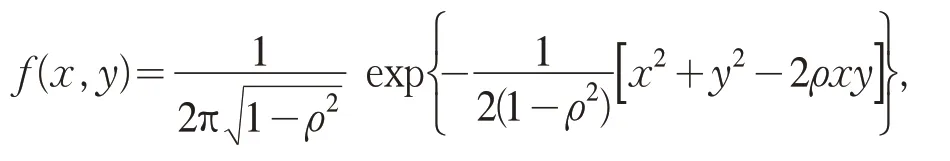
其中(x,y)T∈R2，(X1,Y1)T,(X2,Y2)T,…,(Xn,Yn)T是来自二维正态总体(X,Y)T的n个样本.

假设(X,Y)T的所有矩有限，定义

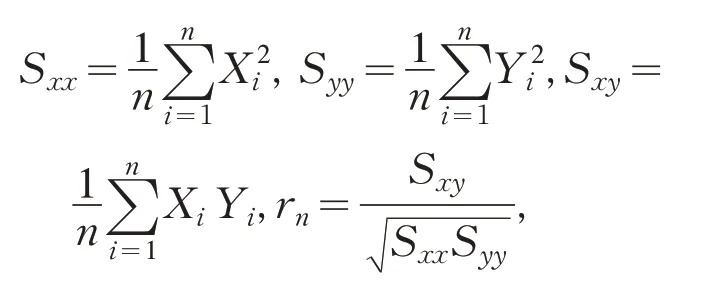
则当n→∞时，

同理cov(X,Y3)=2ρ.

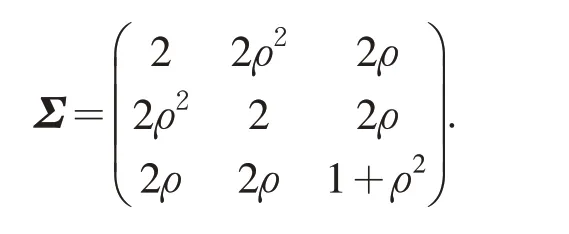
f(b)=ρ，则的极限分布的方差为

说明：定理1仅讨论了特殊情形下二维正态分布样本相关系数的渐近分布，下面讨论一般情况下二维正态分布样本相关系数有关渐近分布的相关结果.

定理2 设总体(X,Y)T服从二维正态分布其概率密度为

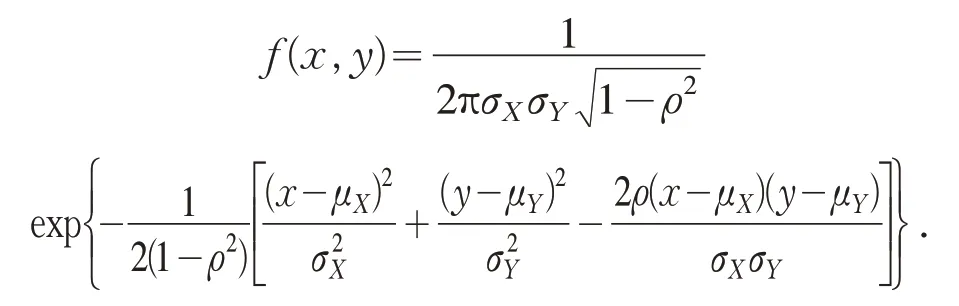
若(X1,Y1)T,(X2,Y2)T,…,(Xn,Yn)T是 来 自二维正态总体(X,Y)T的n个样本.假设(X1,Y1)T所有必要的矩均有限，则

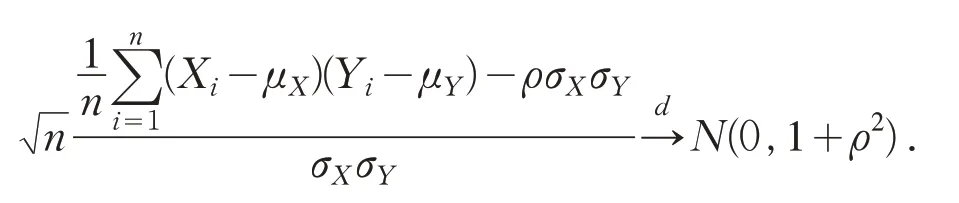
因此得到

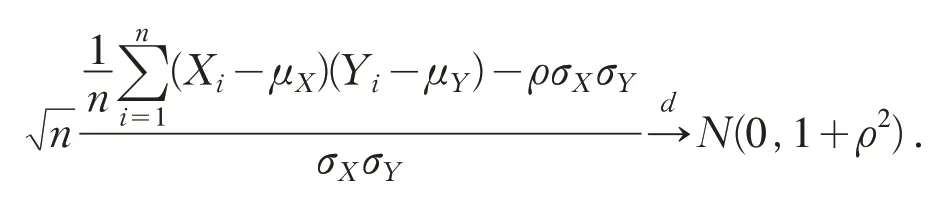
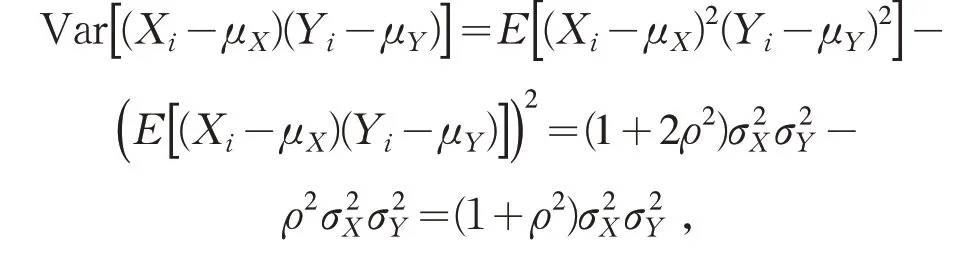
定理3 条件同定理2，并定义

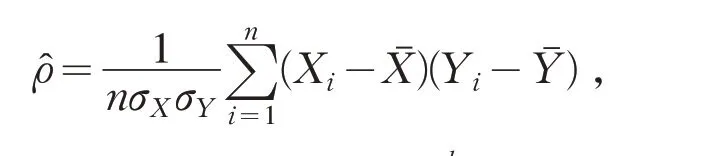
则当n→∞时，

证明 我们有

在定理2中，已经证明了上式的第一项按分布收敛到N(0,1+ρ2) asn→∞.而对于第二项，根据中心极限定理和大数定律，可得

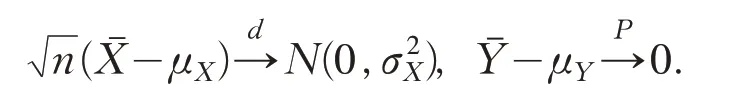
运用Slutsky定理，可得

综合上述情况，并运用Slutsky定理，可得

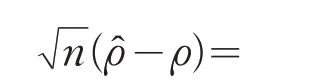
定理4 条件同定理2，假设(X,Y)T的所有 矩 有 限，定 义记则 随 机 向 量的极限分布为三元正态分布其中Σ=

证明 运用中心极限定理可得到

综合上述内容并运用Slutsky定理，可得

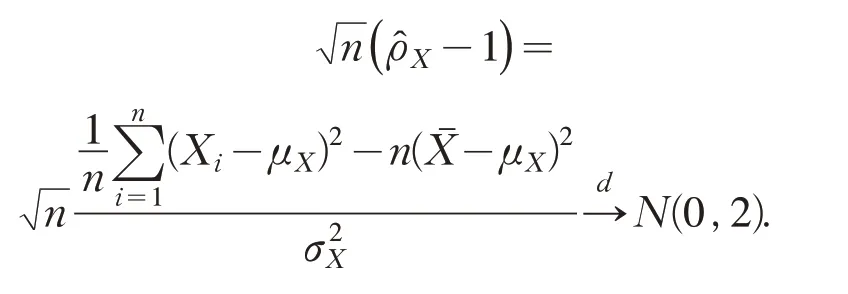
由大数定律，可得

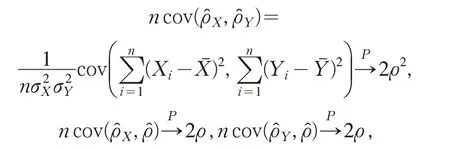
再由定理3和中心极限定理即可得证.

定理5 条件同定理2，并定义

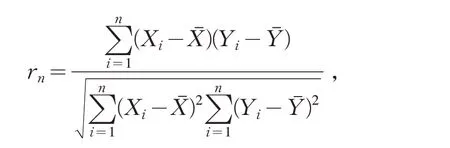
则当n→∞时，

3 结论

众所周知，在统计学领域正态分布的地位举足轻重，主要是因为大量现象或随机变量都可用正态分布描述；当样本量很大时，统计量的极限分布通常用正态分布刻画.二维正态分布总体样本相关系数通常是进行回归分析、主成分分析和因子分析的前提，鉴于此，文章较为详细地研究了部分参数已知和所有参数未知情况下二维正态总体的样本相关系数及其渐近正态性等大样本理论.为进一步研究和应用二维正态分布的样本相关系数的假设检验和区间估计奠定研究基础.例如，利用定理3可以构造部分参数已知时二维正态总体的相关系数的检验统计量或构造渐近置信区间，而定理5可以构造所有参数未知时二维正态总体的相关系数的检验统计量或渐近置信区间.