基于灰靶变换评价大学生就业能力

倪 岚，姚 君，王 奕

对大学生就业能力的评价需要考虑多方面的因素，培养综合素质高、能力强，符合社会需求的毕业生，是当前高等教育的根本目标和主要任务，因此，本文的研究具有十分重要的社会意义.

在实例应用的过程中，首先要考虑的是实验数据的获取方式，灰靶变换方法区别于其他综合评价方法的优势在数据方面的体现是数据量需要很少，不需要使用大量样本数据，就是从解决评判大学生就业能力这一目的本身出发，不是得出具体分数，而是进行排序即可，这种方式非常适合企业在挑选应聘人员时进行少量评价对象的排序.

本文首先构建高校大学生就业能力评价指标体系，在此基础上获取数据，利用灰靶变化方法来评价大学毕业生的就业能力，从而为就业单位评价学生的素质和能力提供依据，同时学校也可以通过反馈后进一步优化学科专业结构，提高人才培养和社会需要的契合度［1-3].

1 构建就业能力评价指标体系

就业能力是使大学生在毕业后能够获得就业机会并维持所胜任工作必需的一系列知识、技能、素质的整合.影响高校大学生就业能力的因素有很多，根据相关文献，综合分析了各种不同的观点之后，初步获得影响就业能力的因素有专业基础知识、人文素质、敬业精神、专业水平、创新能力、实践能力、知识更新能力、应变能力、道德修养［4-10].其中人文素质、敬业精神、道德修养能够反映大学生的内在品质，专业基础知识、专业水平是大学生工作或应聘时所需要的技能，创新能力、实践能力、知识更新能力能够反映出大学生不断创新学习的能力，应变能力能够反映出大学生人际交往和融入团队的能力.综上，构建大学生就业能力评价指标体系见表1.

2 数据的获取

对于高校大学生，对其各项素质水平比较了解的就是老师和同学，所以，通过调查问卷的方式获取数据，选取的问卷调查人有同班级同寝室同学、教授过专业课程的老师和该年级主管辅导员老师.各个评价指标如表1 所示，分数为0～10分，问卷调查人根据自己的标准对所评价的对象打分，精确到小数点后一位.

本文中所评价的对象来源于黑龙江科技大学数学15级1班，首先根据班级学年综测表排名进行间隔为5的分层抽样，共选用6名学生，学生编号为A，B，C，D，E，F，其中A 学生从大一到大四在学习方面投入的精力较多，学习成绩一直名列前茅，在课余生活中没有参加过其他社团或竞赛经历，临近毕业认为自己的能力在社会上竞争力不强，选择并顺利考取了211 院校的研究生.B学生学习成绩一直处于中上游，但有参加竞赛并获奖的经历，平时会阅读专业相关的最新知识和新进展的期刊和文献.C 学生成绩也一直处于中上游，平时社交较为活跃，积极参加社团活动，性格较为外向，乐于交流和分享自己在学习和生活中的想法和经验，也有参与竞赛的经历.D学生学习成绩属于中游，人际交往能力较强，性格外向，与人友善，思维较为发散，愿意钻研，但性格懒散，不注重约束自己，自律性较差.E 学生学习成绩较差，属于散漫的一类，但性格没有明显缺陷和不合群的现象，对大学本科知识体系有一定的认识，但不完善，属于一般大学生的水准.F 同学成绩没有挂科现象但成绩较低，也不是很积极外向的性格，不过对某些专业领域有极大的兴趣，主动进行学习和培训，目前已初见成效，而且选择毕业后继续进行学习.

然后，选择5 名该班的授课教师和5 名本班其他学生进行评价，在平均分数的计算上采取加权平均的计算方法，授课教师与学生的分数权重比为6∶4，各项素质满分为10 分，精确到小数点后1位，具体情况如表2所示.

为保证实验结果的准确性，首先要对调查问卷的信效度进行检验，我们选择利用SPSS20统计软件，使用最常见的内部检验方法中的Cronbach’sα法，检验结果如表3所示.

表1 大学生就业能力评价指标体系

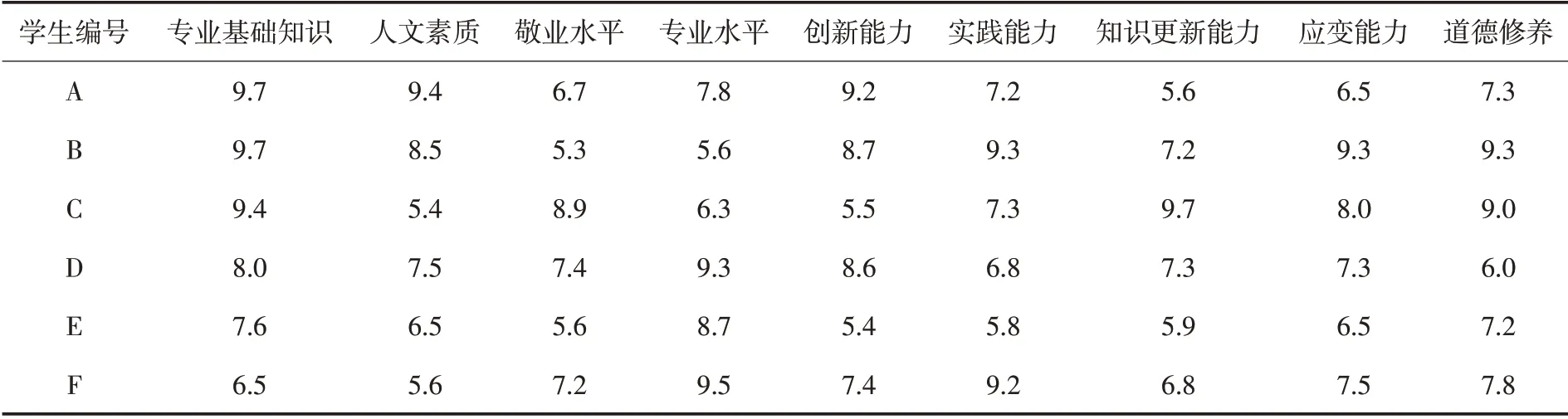
表2 学生就业能力指标评分

表3 可靠性统计量α

由数据可知，α=0.725，整个问卷的信效度处于可以接受的程度.下面利用灰靶变换方法对大学生就业能力进行评价.

3 灰靶变换方法评价大学生就业能力

（2）建立标准模式.因为在评价大学生就业能力的指标因素里，最优效果为极大值，因此，根据上述的评价指标体系，在各个指标向量中选择最优效果因素，将这些极大值构成最优效果向量ω0，即标准模式

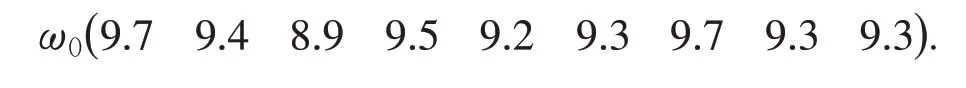
在上述所建立的评价指标体系矩阵中加入向量ω0，构造7×9评价指标矩阵如下：

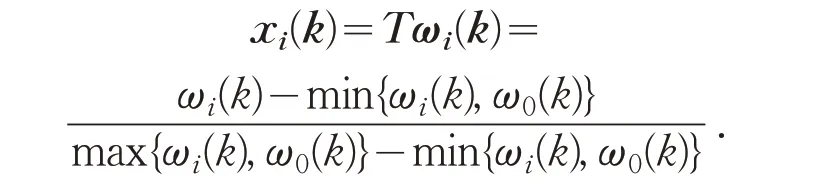
标准模式ω0(9.7 9.4 8.9 9.5 9.2 9.3 9.7 9.3 9.3) 转化为xi(1,1,1,1,1,1,1,1,1)，由公式可得

（4）获得两极差.规范化的评价指标矩阵所得到的灰关联差异信息空间可以表示为

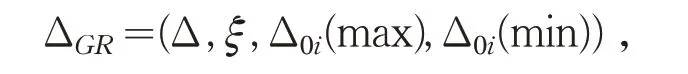
其中，Δ 为全体差异信息，即Δ0i(k)；ξ为分辨系数，ξ∈(0,1) ，在矩阵(Δ0i(k))m+1×n的所有元素中，最大值称为两极最大值Δ0i(max)，最小值称为两极最小值Δ0i(min)，从中可以看出两极最大值Δ0i(max)=1，两极最小值Δ0i(min)=0，因此灰关联差异信息空间是ΔGR=(Δ,0.5,1,0)，其中分辩系数ξ=0.5.

（5）构造靶心系数矩阵.根据公式

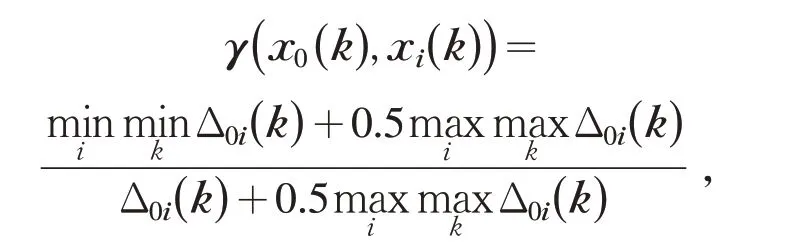
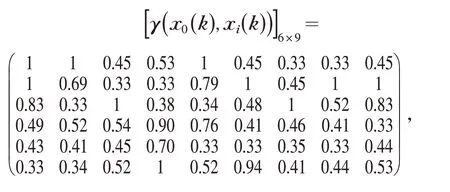
根据构建完成的靶心系数矩阵中的靶心系数计算各个模式与标准模式的靶心度.

将xi的靶心度记为由其中n为评价指标个数，计算靶心度得

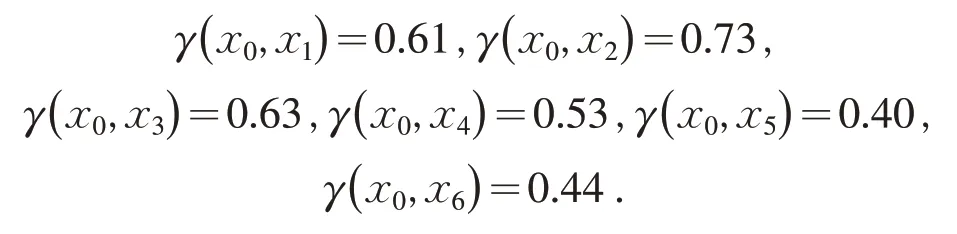
根据灰色关联分析的基本思想，若与标准模式的靶心度越大，则该学生的就业能力则越强，将上面计算得出的靶心度进行排序，得

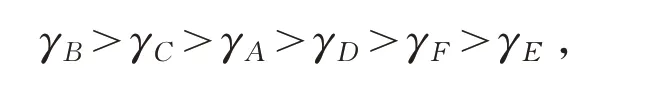
所以编号为B的同学就业能力最强，编号为C的同学次之，E 同学最差.6 名学生的就业能力评价结果如图1所示.

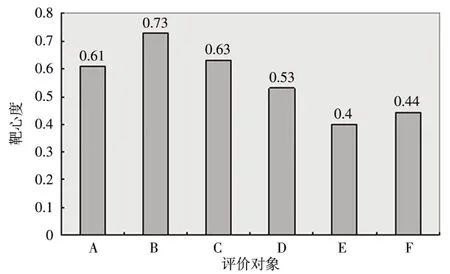
图1 就业能力评价结果

4 总结

得出评价结果后，对被评价对象目前的就业和毕业设计情况进行了统计和总结，如表4所示.

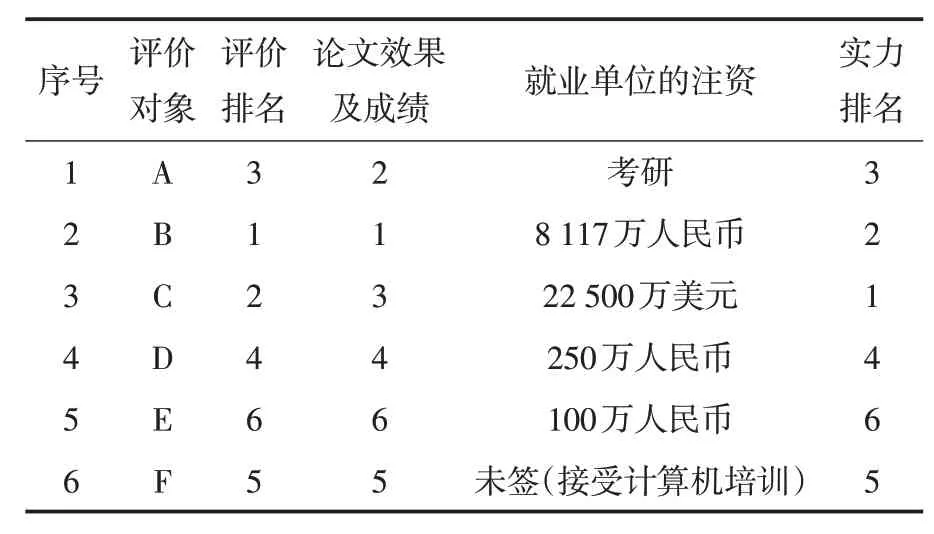
表4 评价结果、论文、就业单位对比

根据上述两点，就业结果和就业能力评价模型的结果基本一致，毕业设计效果方面和模型结果有一定出入，但从学习成绩及相关知识掌握来看仍具有较大的关联，存在B 优于C 优于E 与A优于F的关系基本和模型结果是一致的.

不同于以往在解决综合评价类问题所经常采用的多元统计分析方法，本文所阐述的方法，并不是利用大量数据建立拟合程度好的模型，通过评价指标量来量化高校毕业生的就业能力，而是只针对少数高校大学生的就业能力进行排序，以便用人单位进行比较、参考.可见灰靶变换方法计算简单，实用性强，在评价指标模糊、数据量很少的综合评价问题中具有一定的优势.