定数截尾场合Pareto分布形状参数的最优置信区间

刘 璐，李云飞

(西华师范大学 数学与信息学院，四川 南充 637009)

0 引言

Pareto分布是研究收入模型的一种分布，它最先由意大利经济学家Vilfredo Pareto (1848)提出.Pareto分布在社会经济、军事以及可靠性统计分析等很多领域中得到广泛的应用[1-3].因此，研究Pareto分布在参数估计和可靠性分析上都具有十分重要的理论意义以及实用价值.

关于Pareto分布性质的研究，学者们通过不断地对其进行完善和改进，已经形成了丰富的研究成果：Ouyang[4]对寿命分布为Pareto分布的n个元件进行定数截尾实验，当观测到有r个元件失效后，研究了剩余元件的失效时间以及还需要的实验时间的Bayes预测.李凤[5]基于逐次定数截尾模型，选取未知参数的先验分布为无信息先验分布，分别在平方损失和LINEX损失下，讨论了Pareto分布的形状参数，失效率以及可靠度函数的Bayes估计.王娟[6]给出了Pareto分布中尺度参数的几种区间估计方法，重点研究之前不常见的极大似然估计的渐近正态性法和轮廓似然函数法，并说明这几种方法的适应范围及优缺点.龙兵[7]基于双边定时截尾Pareto分布寿命试验数据，利用极大似然法和EM算法分别计算形状参数的极大似然估计近似值.

而对于最优置信区间的研究也有很多成果，如，李柏林[8]证明了最优区间估计的存在性，并推导出了常见分布形状参数的区间估计公式.田霆[9]在给定的置信度下，求得了定数截尾Weibull分布的形状参数的最短置信区间.李丽颖[10]研究了在总体均值未知时，尺度参数σ及σ2在置信水平为0.90和0.95下的最短置信区间.

定数截尾寿命试验(type-censored sample life test)，又称II型截尾寿命试验，它是指试验到指定的失效个数停止[11-12].国内外的许多学者和专家都对Pareto分布和最优置信区间分别做了相关的研究，但是在定数截尾场合下针对Pareto分布参数最优置信区间的研究较少.本文将通过构造置信区间的一个枢轴量的方法[13]，求定数截尾场合Pareto分布形状参数的最优置信区间，并将其与传统方法求得的置信区间进行对比分析.

1 Pareto分布中形状参数的最优置信区间

1.1 Pareto分布参数θ的置信区间

若随机变量X服从参数为θ和σ的Pareto分布，则X的密度函数为：

f(x;θ,σ)=θσθx-(1+θ)，x>σ，

记为X～Pareto(θ,σ)，其中,θ>0为形状参数，σ>0为尺度参数.

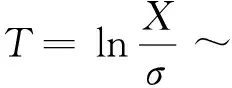
fT(t;θ)=θexp(-θt).

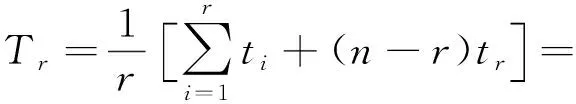
所以

因此，由指数分布的性质可知：枢轴量2rθTr～

χ2(2r).

采用传统方法，对于给定的α∈(0,1)，求得在置信水平为1-α下θ的置信区间：

在给定置信水平的情况下，由于卡方分布的概率密度是单峰非对称，利用传统方法构造的区间是等尾置信区间，而不是最短置信区间，因此造成传统方法所求的置信区间的精度也不高，并且也不是具有一致最小平均长度性质的置信区间.

1.2 最优置信区间

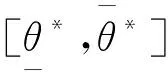
(1)

(2)

1.3 Pareto分布参数θ的最优置信区间

对于Pareto分布而言，在给定的置信水平1-α下，假设存在a,b，其中0

P(a≤2rθTr≤b)=1-α，

由此可得θ的1-α的置信区间为：

这个区间的平均长度为：

(3)

定理1设x1,x2,…,xn是来自总体X的样本，总体X服从Pareto(θ,σ)分布，θ为未知参数，枢轴量2rθTr的分布密度函数为

F在(a*,b*)处的Hessian矩阵为：

因为g′(b*)<0，所以λ*g′(b*)>0，Hessian矩阵为正定矩阵，因此(a*,b*)为非线性规划的唯一最优解.

2 算例分析

假设某种元件服从尺度参数为σ=10，形状参数为θ=0.5的Pareto分布，现从这批元件中随机抽取16个元件进行定数截尾寿命试验，所得的寿命数据[8](单位：小时)按从小到大的顺序排列如下：x1=10.201，x2=11.355，x3=13.507，x4=14.705，x5=23.907，x6=28.327，x7=28.806，x8=32.425，x9=67.62，x10=145.863，x11=230.913，x12=286.61，x13=883.347，x14=1448.172，x15=1635.349，x16=2403.728.在取置信水平1-α=0.95时，求这批元件服从Pareto分布的形状参数的一致最小平均长度的置信区间.

表1 形状参数的最优置信区间

从表1可以发现，最优置信区间长度比传统区间长度相对缩短了ε%(ε与样本个数n无关)；观察发现置信区间相对缩短比率ε%的大小不依赖算例数据，因此该结果具有一般性：当失效个数r≤11时，最优置信区间相比传统的置信区间有较为明显的缩短，幅度在2%～12%；当r>11时，置信区间的缩短比率(<2%)逐渐减小.

3 结论

Pareto分布首先经过线性变换转化成指数分布，然后在定数截尾试验场合中，给出了构造Pareto分布形状参数θ置信区间所需的枢轴量，并且枢轴量服从卡方分布，但是卡方分布的概率密度非对称，从而按照传统方法得到的θ的置信区间不是最优置信区间；因此在这里进一步给出了满足定数截尾试验场合Pareto分布参数θ最优置信区间的条件，并利用拉格朗日乘数法，将最优置信区间求解过程中的非线性规划问题转化为方程问题，由此得到形状参数的最优置信区间；最后给出了一个求解定数截尾场合下Pareto分布参数最优置信区间的算例分析，通过分析发现当失效个数r≤11时，最优置信区间相比传统的置信区间有较为明显的缩短，但随着失效个数r>11，置信区间的缩短比率(<2%)逐渐减小，因此，当r≤11时，可以用最优置信区间作为形状参数的置信区间，这样将会提高估计的精度.