关于“一题多变”在初中数学教学的应用

江苏省新沂市港头中学 黄继梅

“一题多变”，也被称为“一题多式”“变式教学”，是指在教学过程中对所举例题进行拓展和变形，使某一题型由前一种考查模式转换为另一种考查模式，乃至使前一题型转变为另一题型。在新课改背景下，“一题多变”因其发散思维、帮助学生多角度多方面探求问题、迅速夯实学生学习基础的优势，逐渐成为初中数学课堂上的一种常见教学方法。下面，笔者将对“一题多变”在初中数学教学中的应用进行简单论述。

一、“一题多变”运用的意义

1.减轻学习负担，夯实学习内容

在以往的初中数学教学中，教师为了尽可能保证学生掌握所学内容和解题技巧，也为了尽可能覆盖足够多的考试题型，往往采用题海战术。这种做法加重了学生的学习负担，并且容易引起学生畏学、厌学的情绪。

“一题多变”在有限的题目总量的基础上，加大了每一道题目的可变性，从而一定程度上减轻了学生的学习负担。同时，“一题多变”通过对一道题目的不断发散，也利于让学生了解题目设置规律、熟悉题目考查形式。最后，“一题多变”通过对特定题目的反复训练，也能够夯实学生所学内容。此外，“一题多变”的运用，也让数学问题增强趣味性，调动学生的学习兴趣。

2.提高思维能力，提升学习技巧

“一题多变”的有效运用可以帮助学生发展思维能力，提升学习技巧，从而提高学习能力。“一题多变”可以充分提高学生的思维能力，增强其发散思维、化静为动思维、分类讨论思维等在内的多种数学思维。

例如：已知直线l 及其同侧两点A、B，请在直线l 上选一点C，使点C 到点A、B 的距离之和最小。带领学生探讨这个问题之后，教师给出这个问题的变式题，促使学生在理解这个问题的基础上，注重知识的内化、理解和运用。如：已知一条河流两侧有村庄A、B，现在河上修一座与河两岸a、b 垂直的桥，使A 村经B 村的路程最短，请问桥应修在何处？这个变式题中，将一道抽象的轴对称问题转化为了实际应用问题，并将知识点扩散开来，极大地激发了学生的实际应用能力和思维扩展能力。

二、“一题多变”的方法技巧

“一题多变”在初中数学教学中具有积极的作用，但在实际教学中如何进行“一题多变”，仍困扰着一线教师。在这里，笔者从三个方面论述“一题多变”在初中数学教学中运用的方法技巧。

1.改换题设和结论

更改题设和待求结论，是最为常见也最为有效的“一题多变”技巧。例如：如图1，△ABD、△AEC 都是等边三角形，求证：BE=DC。

变式一：如图2，在△ABC 中，分别以AB、AC、BC 为边在BC同侧作等边三角形ABD、ACE、BCF，求证：四边形DAEF 是平行四边形。

图1

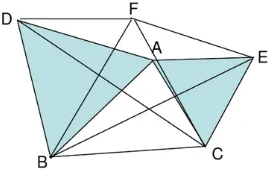
图2

这个变式题，原例只需由“AE=AC，AB=AD，∠BAE=∠DAC”证明△BAE ≌△DAC，从而得证BE=DC；变式一则需由“BD=BA，BF=BC，∠DBF=∠ABC”等证明△ABC ≌△DBF、△ABC ≌△EFC。

这个变式题是在题设和结论上进行了更改，与原例相比，增加了证明角相等、证明平行四边形两组对边相等的内容，在难度和思维性上也大大提高。

但在本质上，两个题目仍然“同源”，题目的主体和考查要点都是三角形全等的证明。尽管两个题目“同源”，但在这样更改题设和结论的过程中，进一步考查学生在几何证明上深入思考的能力，也考查了学生将三角形全等的证明和角相等问题、平行四边形证明问题相结合的能力。因此，变式题升华了原题，利于学生综合能力的提升。

2.延伸问题和思考

在“一题多变”中，对结论进一步加深思考，从而将原问题进行延伸，引导学生进行进一步的思考，也是一种常用的方法技巧。

例如：在半径为5 的☉O 中，弦AB 的长为8，且点P 在AB 上，求OP 长度的取值范围。

变式一：在半径为5 的☉O 中，弦AB 的长为4，且点P 在AB 上，若OP 长度为整数，则点P 的个数为多少？

变式二：点P 在半径为5 的☉O 中，若OP 长为3，则经过点P的所有弦中，弦长为7、8、9 的弦各有几条？

这个例题中，对圆中一弦上点到圆心的长度OP 的取值范围进行了讨论，变式一则将OP 进一步限定在整数范围之内，从而求P 点个数，变式二则更进一步，将OP 限定在固定长度，反求过P 的弦长。这三个问题每一问都是前一问的延伸和扩展，充分向学生展示了这一问题的一些基本考查角度，也能够让学生在不断深入思考的过程中，对弦长问题有更进一步的了解。

3.遵循由浅入深

“一题多变”中，对于某一数学问题的讨论，由例题的浅层次“初探”，到不断变式的深层次“细究”，带领学生开展由浅入深的数学学习，也是一种不错的方法技巧。

以上面的圆的问题为例，教师可以在变式一、变式二的基础上，进一步给出变式问题，逐渐加大难度，不断提升学生的思维力。如：

变式三：在半径为5 的☉O 中，弦AB 与CD 平行，若AB=8，CD=6，则AB、CD 间的距离是多少？

变式四：在半径为5 的☉O 中，梯形ABCD 内接于☉O，且AB ∥CD，若AB=8，梯形的高为1，则CD 长为多少？

这两个变式是例题三及其变式一、二的进一步深入讨论，开始探讨圆内一弦与另一弦之间的位置关系，引导学生开始由对弦与其上一点问题的探讨转为两弦之间的讨论，逐渐由浅入深，对圆内图形关系进一步进行了研究。

总之，“一题多变”对于初中数学教学具有实践意义，教学中，教师应善于使用“改换题设和结论、延伸问题和思考、遵循由浅入深”等方法技巧，切实用好“一题多变”这一教学利器，打开学生的思维通道，发展学生综合能力，提升数学教学效果。