基于数学理解性学习的计算教学实践

江苏省江阴市敔山湾实验学校 钱 博

《数学课程标准》指出：数学知识的教学，应注重学生对所学知识的理解，体会数学知识间的关联。学生掌握数学知识，不能死记硬背，应该以数学理解性学习为前提。所谓数学理解性学习，是指学生在理解基础上的数学学习，也即通过这样的学习使学生获得了对数学的理解。

数学理解性学习追求的是在数学学习的历程中对数学的理解不断深入与拓展。数学理解的形成是一种不断发展的层级递进过程。吕林海教授提出了数学理解性学习的层级发展的过程模型，即学生在数学学习的过程中，会相继经历经验性理解、形式化理解、结构化理解和文化性理解四个发展阶段。下面以计算教学为例，谈谈在实际教学中，借助层级发展的过程模型来促进学生数学理解性学习的教学策略。

一、联系旧识，丰富经验性理解

经验性理解是学习者在自身经验的基础上对学习对象最初的理解。对于数学学习来讲，经验性理解通常发生在学习的初始阶段。因此，发展学生的经验性理解，一方面要注意从学生已有的知识经验出发，联系旧知，另一方面要关注知识组织的形式和呈现的方式。以“分数除法计算”为例，学生对于分数除法计算并不是一无所知，分数乘法、倒数、商不变的规律等，都是学生在学习中积累的知识经验。因此，从学生数学理解的角度出发，设计开放性的问题和熟悉的问题情境，可以有效地激活学生已有的知识经验，为学习分数除以整数提供现实基础。

【片段一】

1.复习分数乘法。

（1）口算。

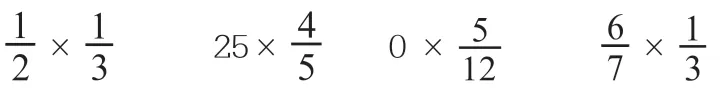
复习分数乘法的计算方法。

（2）练习。

通过以上练习让学生明白：求1 除以某个数的商就是求某个数的倒数。

2.探究不同算法。

师：大家想出了这么多解决的办法，这些方法都正确吗？请你说出理由。

3.优化算法，总结归纳。

师：同学们说的这5 种方法殊途同归，结果都是正确的。这里的每一种方法都运用了转化的数学思想方法，转化是一种非常重要的数学思想方法。你觉得在这几种方法中，哪一种方法最好？

学生先讨论，再说明理由，最后归纳出分数除以整数的计算法则。生1：分数除以整数，就等于分数乘以这个整数的倒数。

生2：这个整数不能为0，因为0 是没有倒数的。

……

教师没有预先给定材料和方向，而是给予学生充分的时间思考，创设富有挑战性的问题情境，让学生运用已有的知识经验独立思考，尝试探究，获得计算方法。学生通过自己的努力，创造出比书本给出的还要多的几种计算方法，体验到了解决问题的乐趣，特别是学生运用商不变的规律来解决问题，将以前学到的知识与新学到的知识联系起来，在新旧知识的连接点上发展了新知，同时渗透了“转化”的数学思想。

二、抓住本质，实现形式化理解

学习者对自身经验知识中的各种刺激进行整理、组织、概括与重新表征，学习者摆脱经验认识中的非本质属性，而直达知识的本质，经历“数学化”的过程，借助抽象与建模，让学生的学习上升到形式化的理解。以“乘法分配律”为例，让学生通过理解乘法的意义去掌握乘法分配律的算理和算法，把握乘法分配律的本质，使学生能够深入理解乘法分配律的数学模型。

【片段二】

师：这里式子不同，结果却是相等的，你知道这是为什么吗？

生1：这里的两个式子都是表示四年级和五年级一共要领跳绳的根数，所以结果相等。

教师引导学生结合图形说出自己的想法，课件演示，把实物抽象成图形。

生2：因为6×24 表示6 个24,4×24 表示4 个24，把它们加起来就是10 个24，而（6+4）×24 就表示一共有10 个24，所以结果相等。

师：听明白了，你是从乘法的意义去理解（6+4）×24=6×24+4×24，所以不计算也能知道它们的结果是相等的。

师：（6+4）×24=6×24+4×24，从右往左可以怎么说？

师：比较等号两边的式子，有什么相同点和不同点？

生1：左右两边都有乘法和加法。

生2：（6+4）×24 是先算加法，再算乘法，6×24+4×24 是先算乘法，再算加法。

师：你能再写出两个这样的式子，说一说每个式子分别表示什么吗？

教师引导学生写出等式，运用乘法的意义来判断等式的左右两边是否相等。学生从计算和乘法的意义两个知识层面理解相等的道理，有利于学生自主建构和理解乘法分配律的模型，把握知识的本质，对乘法分配律的认识由感性到理性，实现对数学内容本质的理解。

三、知识迁移，促成结构化理解

结构化理解是一种形成结构关联的理解，学生在知识关系的脉络中把握知识的本质与内涵，从而形成一个知识链和知识整体结构，比形式化理解更进一步。以“小数乘整数”为例，学生通过沟通联系，出现多种方法计算。

【片段三】

师：会计算0.8×3 吗？请你试一试。

学生独立计算后交流。

生1：0.8+0.8+0.8=2.4。0.8×3 表示3 个0.8 相加。

师：看起来小数乘法的意义和什么是相同的？

生：整数乘法。

生2： 0.8元=8角，8×3=24（角），24角=2.4元，也就是0.8×3=2.4（元）。

师：运用单位名称的换算，把小数转化成整数，再计算。

生3：0.8 是8 个0.1，3 个0.8 是24 个0.1，是0.8。

师：看成24 个0.1 来计算，这个结果是否正确呢？我们借助图形来验证一下结果。

小数乘法与整数乘法有着密切的联系，把整数乘法的意义，整数乘法的计算方法与小数乘整数联系起来，理解小数乘整数的算理和算法，形成一条完整的知识体系链，教学中让学生回顾、梳理，运用已学的知识，帮助学生把新知纳入自己的整体知识结构中，深化对数学的理解。

四、拓展应用，渗透文化性理解

文化理解是一种对数学的综合的、整体性的理解。数学作为一种文化，它蕴含着久远而深刻的思想方法，对社会发展具有重要的推动作用和独一无二的美，无疑对学生的数学学习具有重要的价值。以我国明朝的《算法统宗》中“铺地锦”的乘法计算方法为例，学习了两位数乘两位数后，在教材的“你知道吗”中介绍了“铺地锦”， “铺地锦”因其计算时画出的格子类似先人制造的地锦而得名。

【片段四】

师：在上课前，很多同学来问我什么是“铺地锦”？它的计算方法是怎样的？

开场白结束后，学生A就立刻站起来说：“老师，我知道什么是‘铺地锦’，我把计算方法讲给大家听。”

他自信地来到讲台上，计算62×35，先把乘数分别写在方格的上面和右面，然后把一个乘数各位上的数相乘，积写在相应的方格里，像6 乘3 得18，写在左上方格里，再把斜对着的数分别相加，就得到相乘的积为2170。

师：你们觉得这样计算对吗？

生列竖式计算，检验。列竖式计算后，大家一致肯定。

师：将竖式算法与“铺地锦”的算法比一比，有什么发现？

生1：竖式计算，先算5 乘62，而“铺地锦”的计算顺序是先算3 乘62。

师：为什么这两种算法中有这么多不同之处，却不影响答案呢？接下来，大家小组合作，一起探索。

生：分析竖式计算过程的每一步，可以发现在“铺地锦”中出现的数，同样在竖式计算过程中也会出现，这些计算过程在竖式计算中是口算的，省略了。

师：原来两种算法是相通的。

数学文化通过感悟，让学生对知识及其脉络形成深刻理解，引导学生回溯知识的源头，展现知识真实的发展过程，触摸到知识的本质，深化理解，感悟数学文化的魅力。

学生或许知道很多数学知识，但并不一定真正理解数学的本质。计算教学不能教授机械的算法和规则，要给予学生各种机会，在解决问题和交往互动中达到对算理、算法的深度理解。从关注双基到走向理解性的学习，是数学学习的一种价值回归。