2019年高考数学北京卷理科第18题的多解及推广

广东省云浮市邓发纪念中学 (527300) 林朝冰

原题再现(2019年高考北京卷理科第18题)已知抛物线C：x2=-2py经过点(2，-1)．

(Ⅰ)求抛物线C的方程及其准线方程；

(Ⅱ)设o为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M、N，直线y=-1分别交直线OM、ON于点A和点B．求证：以AB为直径的圆经过y轴上的两个定点．

1.一题多解

(Ⅰ)略，下面主要阐述(Ⅱ)的解法.

1.1 标准方程法

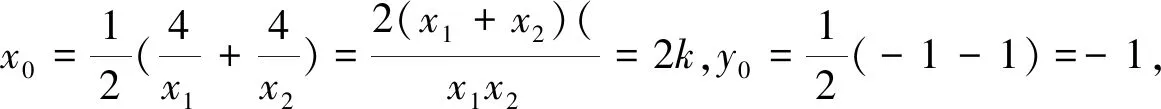
当x=0时，4k2+(y+1)2=4(k2+1),所以y=1或y=-3.所以以AB为直径的圆经过y轴上的定点(0,1)和(0,-3).

1.2 向量法，通过证明直径上的圆周角是直角来实现

1.3 利用圆相交弦定理的推论DF2=AF·BF

-3.故以AB为直径的圆经过y轴上的定点(0,1)和(0,-3).

2.一般化推广，将原题中的抛物线方程一般化，并将原题中直线l与直线y=-1的交点任意化

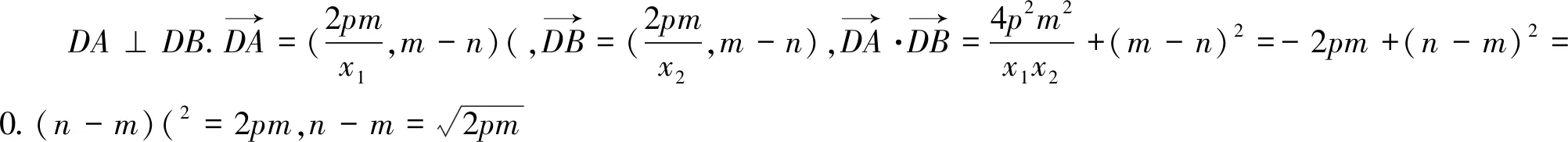
显然，当抛物线的焦点位于x轴上时，也有类似性质.

3.类比推广，将结论推广到椭圆和双曲线

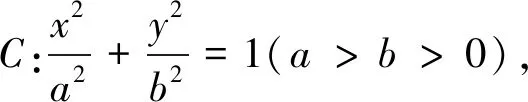
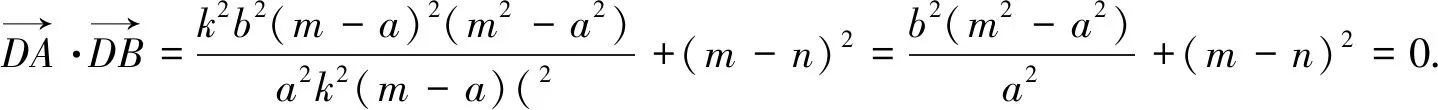
显然，当椭圆的焦点位于y轴上时，也有类似性质.

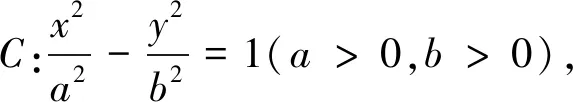
推广3的证明方法与推广2类似，在此不再赘述.显然，当双曲线的焦点位于y轴上时，也有类似性质.

4.改变条件，将推广引向深入

推广1、2、3都对m的取值进行了约束.以推广2为例，要求-aa结论还成立吗？

从图形上看，|m|>a且斜率不等于0的直线l与椭圆有交点时，交点M、N同时位于x轴的上方或下方，直线A2M、A2N与直线x=m的交点A、B同时位于x轴的上方或下方，所以DA与DB不可能垂直.

若直线l的斜率等于0呢？从图形上看，当直直线l的斜率等于0时，点N与右顶点A2重合，进一步大胆设想，将推广2中的动点M、N换成定点，即换成椭圆的左、右顶点A1、A2，定点A2换成椭圆上的动点M，这时，直线MA1、MA2与直线x=m的交点A、B就分别位于x轴的上下两侧了！会不会有类似结论呢？经证明，得出以下结论.

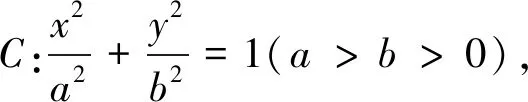
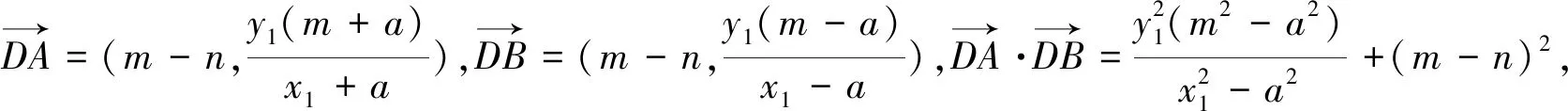
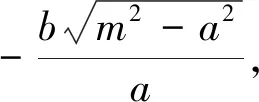
显然，当椭圆的焦点位于y轴上时仍有类似性质.

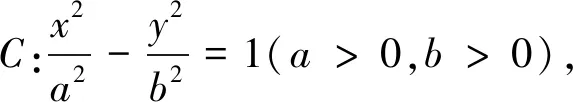
推广5的证明方法与推广4类似，在此不再赘述.显然，当双曲线的焦点位于y轴上时仍有类似性质.

5.再一次类比推广

将推广4、5中的椭圆、双曲线换成抛物线时，由于抛物线只有一个顶点，可以认为另一个顶点在无限远处，此时它与抛物线上的动点M的连线与对称轴平行，因而得到以下推广.

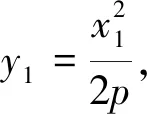
显然，当抛物线的焦点位于x轴上时，也有类似性质.

6.结语

《普通高中数学课程标准(2017年版)》提出,“高中数学教学要以发展学生数学学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质.”学生的核心素养的形成并不能一蹴而就，它是在日常的课堂教学中逐步形成的.解题教学是中学数学必不可少的内容，事实上，题目也是一种数学情境，因而，教师要精心设计，以达到激发学生学习数学的兴趣，启发学生思考的目的.一题多解，多角度推广就是一种很好的解题教学方法，它既能激发学生学习兴趣，启发学生思考，又能避免学生深陷“题海”.