例析化归法求解函数导数问题

江西省鹰潭市第一中学 (335000) 黄鹤飞

化归法就是将待解决的问题和未解决的问题，采取某种策略，转化归结为一个已经解决的问题；或归结为一个熟知的具有确定解决方法和程序的问题；或归结为一个比较容易解决的问题，最终求得原问题的解.本文例举其在解决函数导数问题中的运用.

例1 已知函数f(x)=lnx-ax2(a∈R).

(1)讨论y=f(x)的单调性；

(2)若函数f(x)有两个不同零点x1，x2，证明：x1x2>e．

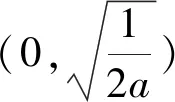
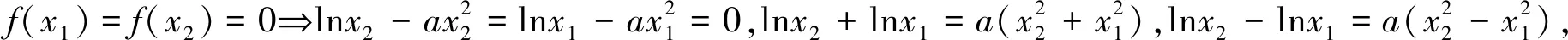
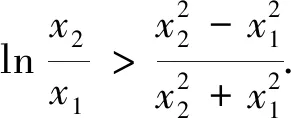
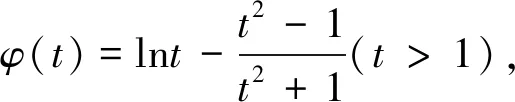
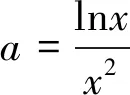
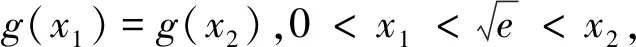
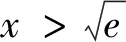
评注:本题(2)主要考查利用导数研究零点及利用导数证明不等式问题，求解中采用了换元法、等价变换法进行化归转换法.

例2 已知函数f(x)=x2(6lnx-4x+6a-3)有两个极值点.

(1)求a的取值范围；

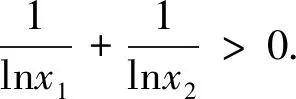
解：(1)由f(x)=x2(6lnx-4x+6a-3)，得f′(x)=12x(lnx-x+a).函数f(x)有两个极值点等价于f′(x)=0在(0,+∞)上有两个零点，等价于lnx-x+a=0在(0,+∞)上有两个零点.

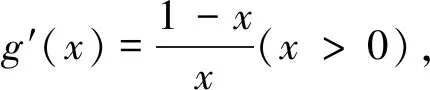
当a≤1时，g(x)max≤0恒成立，f(x)在(0,+∞)上单调递减，不可能有两个极值点，舍去；

当a>1时，e-a∈(0,1),ea∈(1,+∞),g(e-a)=-e-a<0,g(ea)=2a-ea<0，而g(1)>0，由零点存在性定理得g(x)在(0,1)和(1,+∞)内分别存在一个零点，此时f(x)有两个极值点.综上，所求a的取值范围为(1,+∞).

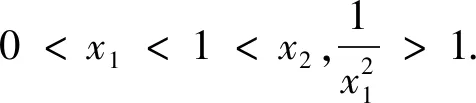
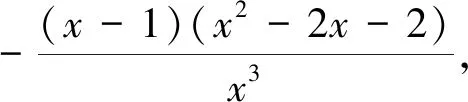
评注:本题为导数在函数中的综合应用问题,主要考查到利用函数极值求参数范围及利用极值点证明不等式问题，其求解中重点考查到化归方法的应用.

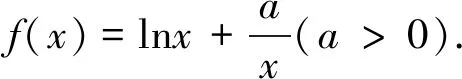
(1)若函数f(x)有零点，求实数a的取值范围；

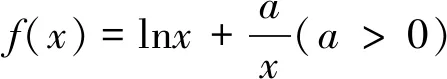
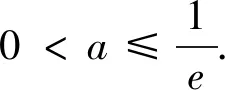
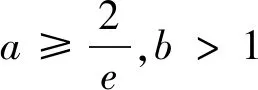
评注:本题除考查导数在函数中的恒成立问题，也考查了利用导数研究函数的零点问题，并考查了利用函数的极值求参数范围，采用换元构造法构造新函数研究恒成立等问题，其求解过程中重点是运用了化归法,将问题不断朝求解方向转化.