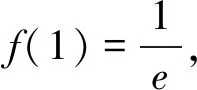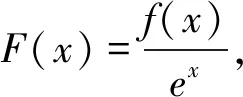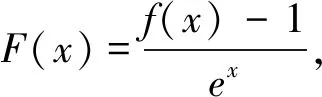一类与导数有关的抽象函数不等式问题的解法
湖北省黄石市第七中学 (435000) 谷文俊 刘静平
在高三二轮复习过程中,学生经常能碰到已知条件为抽象函数及抽象函数导数的不等关系,然后求抽象不等式解集或判断大小关系的题.学生在解决这类问题的的时候,面对常见和简单题时还能做出来,但稍微复杂点的题就会出现下不了笔的情况,主要原因是随着已知条件中的抽象函数导数不等关系的变化,学生不能合理的构造新的函数,然后利用新函数的单调性解决面对的问题.本文结合在教学过程中碰到的问题,并对问题进行梳理,归纳总结出一些常用的解题方法.
一、构造f(x)·g(x)或类型函数
例1 设f(x),g(x)分别为R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0且g(-3)=0,则f(x)·g(x)<0的解集是.
解析:由已知条件可构造新函数F(x)=f(x)g(x).当x<0时,F′(x)=f′(x)g(x)+f(x)g′(x)>0,所以F(x)在(-∞,0)单调递增.又F(-x)=f(-x)g(-x)=-f(x)g(x)=-F(x),所以F(x)为奇函数.从而F(x)=f(x)·g(x)<0的解集为(-∞,-3)∪(0,3).
例2 (2015年全国卷理科)设f′(x)为f(x)的导函数,f(x)在R上为奇函数,f(-1)=0,当x>0时有xf′(x)-f(x)<0,则使f(x)>0成立的x的范围为.
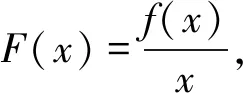
例3 已知f(x)是定义在(0,+∞)上非负可导函数,且满足xf′(x)+f(x)≤0,对任意的正数a,b,若a A.af(b)≤bf(a)B.bf(a)≤af(b) C.af(a)≤f(b)D.bf(b)≤f(a) 注:当已知条件中有结构类似于f′(x)g(x)±f(x)g′(x)的不等式可以构造这种类型的新函数.通过求导判断新函数的单调性,利用单调性比较大小解不等式或者利用函数的图像特点得到不等式的解集. 例4 (2015年福建卷)若定义在R上函数f(x)满足f(0)=-1,其导函数f′(x)满足f′(x)>k>1,则下列结论中错误的是( ). 注:当已知条件中有结构类似于f′(x)±a的不等式可以构造这种类型的新函数.在构造新函数的过程中,可以结合题目的特点考虑新函数的后面有常数k,以方便计算. 例7 定义在R上函数f(x)满足f′(x)>1-f(x),f(0)=6,则ex·f(x)>ex+5的解集为. 解析:可构造函数F(x)=ex·f(x)-ex,利用由f′(x)>1-f(x)可得F(x)=ex·f(x)-ex在R上单调递增.又因为ex·f(x)-ex>5,F(0)=e0f(0)-e0=5,则F(x)>F(0),所以ex·f(x)>ex+5解集为(0,+∞). 例8 已知f′(x)为f(x)的导函数且f(0)=0,对任意实数x恒有f(x)>f′(x)+1,求不等式f(x)+ex<1的解集为. -1,则F(x) 例9 已知f′(x)为f(x)的导函数且2f(x)+f′(x)>2,f(0)=8,求不等式f(x)-7e-2x>1的解集. 解析:构造函数F(x)=e2x·f(x)-e2x,由2f(x)+f′(x)>2可得F′(x)=e2x(2f(x)+f′(x)-2)>0,所以F(x)=e2x·f(x)-e2x单调递增.对f(x)-7e-2x>1变形有e2xf(x)-e2x>7.又因为F(0)=7,则F(x)>f(0).所以f(x)-7e-2x>1的解集为(0,+∞). 注:当已知条件中有结构类似于f′(x)±f(x)的不等式可以构造这种类型的新函数.构造新函数的过程中要不断的尝试,且特别要注意ex求导的特点.对复杂不等式,要结合新函数的结构特点对不等式进行变形,将其变成与新函数表达式有关的形式,再利用单调性比较大小,求出不等式的解集.
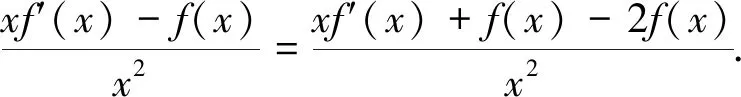
二、构造f(x)±g(x)+k类型函数
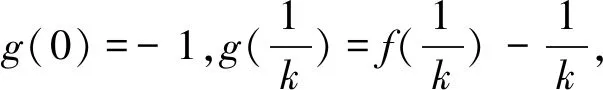

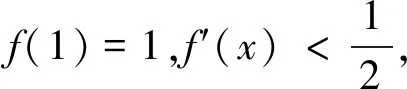

三、构造ex·f(x)或类型函数