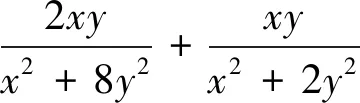对一道高考试题的多视角“消元”

四川省成都经济技术开发区实验中学校 (610100) 杜海洋

纵观近几年全国各省市的高考题或模拟题，几乎都有一道涉及求最值或值域的选择题或填空题，多为容易题或中档题.这些题型往往结构小巧玲珑，题干简洁、精炼、优美.对考生来讲如何快速、灵活、准确地破解这类小题体现了考生平时掌握解题的基本功.2019年高考天津卷第13题是以一道求代数式的最值呈现，中规中矩，是对学生掌握求最值问题的一道“体检”题.

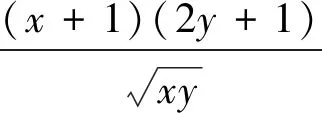
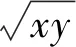
方法一 基本不等式法直接消元

解：因为x>0，y>0，x+2y=5，则

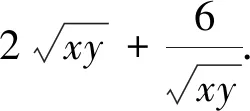
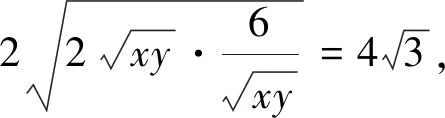
点拔：由已知条件，先将式子中的分子展开后化简，再由式子结构特点直接利用均值不等式求最值，积为定值或和为定值体现直接将“元”化常数，当然此法尤其注意等号成立的条件.

方法二 整体消元建立函数用导数法

点拔：作为高考题，重点是考查学生运用均值不等式取最值时条件是否成立.处理等号不成立问题，导数法是解决这类问题的主要手段，也是我们平常说的对勾函数的运用.

方法三 三角换元法

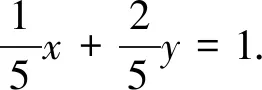
点拔：求最值时涉及到有界性问题及消元思想，三角代换往往排上用场.尤其是题中出现式子变形化为和为1时，用三角函数思想进行代换消元.

方法四 改变式子结构再用基本不等式消元

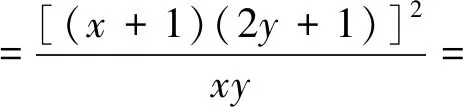
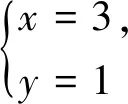
点拔：已知条件结构形式与所求式子相互转化是探究问题的常见手段之一，即未知向已知转化，此法与法一殊途同归，但体现了出题者对试题的宽入口完美体现.

方法五 构造等差数列消元

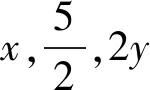
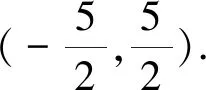
点拔：在条件出现等式形式，不管涉及和与差，可以联想到等差数列，从而进行消元思想进行处理.

方法六 整体代换建立一元二次方程利用判别式

点拔：不等向等式转化这是解决数学问题常用方法，尤其涉及求代数式的值或值域，将代数式看成一个整体进行消元，如式子出现项与项由明显的二次关系时，往往从二次函数或一元二次方程角度去破解.

方法七 由等式直接代换消元

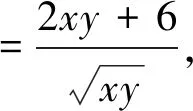
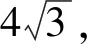
点拔：含有多参数式子，利用已知条件消参数应该是解答数学试题的最基本思路之一，即消参法.有时可将式子中的一个式子看成一个元素进行消参，比如方法二、方法六.

3.解题反思作为在平时教学中如果我们解答往年的高考真题，如果停留在参考答案这里，学生常常会疑问平时学的求最值方法去哪儿了？此题导数法行不?消元法、代换法、判别式法等等行不？通过对此题的多解的分析与呈现，目的是扩展学生们的思路，找到问题的突破点，思维的目标划归为——消元策略，再将解答之间的方法进行比较，从而找准此题型的优解.如何从不同角度分析问题，广泛联系所学的数学知识，从而提高解决此类问题的能力，才能在高考解题中运用自如.

4.反馈练习

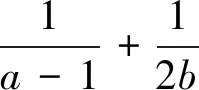
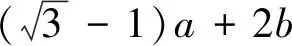
(3)已知x>0，y>0，x+2y+2xy=3，则x+2y的最小值为．