2019年高考解析几何试题分析与教学启示

福建闽清教师进修学校 (350800) 黄如炎

2019年高考加强了对解析几何的考查力度，六套全国卷中普遍把解析几何作为压轴题，突出了圆锥曲线定义、数形结合思想、坐标化与运动变化方法、甄选直线方程等解析几何学科本质的考查，充分体现了逻辑推理、直观想象、数学运算和数学抽象等核心素养的命题导向．本文通过试题特点分析和典型试题研究，给出解决解析几何问题的基本通径和重要经验，期望能给教师教学提供帮助．

1.试题特点

2019年高考解析几何试题具有以下特点：

(2)试题具有“三无”特点，即无图形、无点坐标、无直线方程，考生解题要从画图、设点坐标和选择直线方程开始．

(3)全国卷明显加强了对解析几何的考查．解析几何试题的题序后移，普遍将解析几何作为压轴题进行考查，如文科Ⅰ卷、Ⅱ卷在第12题，理科Ⅰ卷在第16题，文科Ⅰ卷、Ⅲ卷和理科Ⅱ卷、Ⅲ卷在第21题考查解析几何，这种对解析几何的考查力度前所未有．把解析几何作为压轴题改变了传统以函数与导数为压轴题的做法，有利于改变因对某主干内容考查过热而导致对其进行反复操练的教学行为，有助于打破僵化的应试教育．

(4)加强了对双曲线的考查，全国Ⅰ卷、Ⅱ卷、Ⅲ卷文理科试卷都在客观题中考查双曲线的标准方程和几何性质(离心率、渐近线、对称性等)．

(5)突出了圆锥曲线定义、数形结合思想、坐标化与运动变化方法、甑选直线方程等解析几何学科本质的考查，体现了逻辑推理、直观想象、数学运算和数学抽象等核心素养的命题导向．

(6)选填题主要考查圆锥曲线定义、标准方程和简单几何性质．解答题重点考查直线与圆锥曲线的位置关系，切入容易深入难．第一步大多是在给定条件下求直线或圆锥曲线方程，比较容易．第二步基本是利用第一步的结果解决定量(如斜率、弦长、面积、定值、最值等)或定性(如定点、定直线、存在性、探索性等)问题，常与平几、向量、三角、函数、导数、不等式和数列等知识综合．

(7)全国Ⅰ卷文、理科数学试卷对解析几何的考查还存在一定的差异，全卷相同试题也只有三分之一．2021年新高考数学不再文理分科而使用同一张卷，如何逐渐向文理同卷过渡，契合新课程理念，需要命题人员和一线教师思考．

2.试题解析

例1 (2019年全国Ⅰ卷文科第12题)已知椭圆C的焦点为F1(-1,0)，F2(1,0)，过F2的直线与C交于A，B两点.若│AF2│=2│F2B│，│AB│=│BF1│，则C的方程为( ).

图1

图2

图3

除了例1、例2外，还有许多试题都可通过回归定义与数形结合快速求解．

(1)求C的方程，并说明C是什么曲线；

(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.(ⅰ)证明：△PQG是直角三角形；(ⅱ)求△PQG面积的最大值.

解析:(1)易求C方程为x2+2y2=4(x≠±2)，C是中心为原点，焦点在x轴上的椭圆(不含长轴的端点)．第(2)步分析如下：

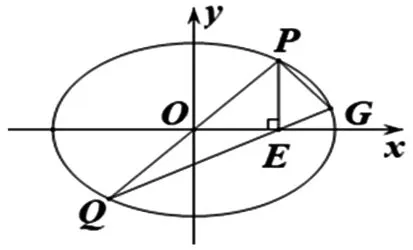
图4

思路1:如图4，△PQG是随动直线PQ的变化而变化，即△PQG是由直线PQ决定的，故以直线PQ的斜率为源变量解题，研究的具体路径为：设直线PQ方程为y=kx→由点P所在的直线PQ和椭圆C的方程求出P点坐标，由点G所在直线QE和椭圆C的方程求出G点坐标→把几何问题“PG⊥PQ、△PQG面积”用源变量k表示→ 通过代数运算解决问题．

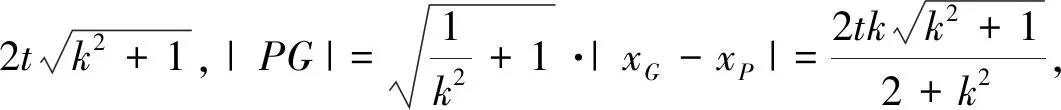
思路2：△PQG由点P的变化而变化，故也可用P点坐标为源变量，具体解决路径为：设P(m,n)，则Q(-m,-n)，E(m,0)→由点G所在的直线QE和椭圆C的方程求出G的坐标→把几何问题“PG⊥PQ、△PQG的面积”用源变量m,n表示→通过代数运算解决问题．

解析5:(ⅰ)同解析4.

3.教学启示

解析几何试题一般都不给出图形，解决问题是从正确画图开始的．学生如果没有画出正确图形，可能会影响问题的思考．在例1不准确的图1中就无法得到B点坐标，例2如果没有正确的图3，就难以利用平几知识快速解题．因此要求学生正确画图，养成边推理边修正图形的习惯，利用几何直观助力问题思考，提高逻辑推理和直观想象素养．

圆锥曲线定义是圆锥曲线的本源，对涉及焦半径的问题利用定义干脆利落．平面解析几何研究的是平面几何问题，研究时离不开‘形’的特征，以形助数，常能秒获答案，无需代数之运算．数形结合是优化思维性，减少运算量的利器．回归定义和数形结合可谓相得益彰，是解题途中的最美风景，学生切勿“忘本忘形”．例1、例2的解法是回归定义与数形结合的典范．

美籍数学家柯朗认为：“解析几何的基本思想是引进‘坐标’，即对一个几何对象附上或标上数，从而完全刻画了这个对象”[1]．解析几何的基本思想是坐标化与运动变化思想，因为解析几何是源于自由落体、行星运动和抛物线的研究，是创立于运动变化观点上的学科．运动变化时某些变量(如动直线的参数、动点坐标等)是变化的内因，其它变量因它的变化而变化，不妨把这样的变量称为源变量．研究直线与圆锥曲线位置关系问题可通过引入源变量，用源变量表示直线与圆锥曲线的交点坐标和几何问题，通过代数运算解决几何问题．研究通径为：引入源变量(如动直线斜率、动点坐标等)→由点所在的直线、曲线方程求出其坐标或坐标间的关系式→用源变量表示几何问题→经过代数运算解决几何问题．例3的思路是解决解析几何问题的基本通径，也是用运动变化思想研究解析几何问题的典范．用运动变化的思想研究解析几何，有根、有序、灵动、鲜活．

由于同一个点可视为不同直线和圆锥曲线的交点，因此如何选择直线也要依题情进行判定．如例3点G可看成直线QE和椭圆C的交点，也可看成直线PG与椭圆C的交点．要求G点坐标，由于直线QE比直线PG的方程简单，故选择直线QE．但思路3要求xG+x1时，就要选择直线PG．

此外，源变量的选择也影响解题的难度和计算量，所选源变量要便于表示几何关系．

解析几何坐标化后的代数运算要先仔细观察数式结构特征，遵循数式运算法则．要注意多项式的因式分解、同类项的展开合并、分式的通分(或去分母)、公因式(公约数)的提取(或约分)、多元的消元、同一代数式多次运算的换元、去括号的是否变号等，做到且看且算，且算且思．对运算教师要进行板演示范，不可用“整理得”省略去学生可能出错的计算，板演要抓住切入点、把握思维点、强调易错点和呈现得分点．但学生运算能力不可能完全通过听和看就能形成，务必在踏踏实实的运算实践中进行锻炼．

解决解析几何问题需要综合思维，为避免学生“忘本忘形”和顾此失彼，达到顺畅解决问题，教师可引导学生概括出解决解析几何问题的重要经验：回归定义不可忘，数形结合成习惯，选择直线要判断，数式先看后运算[2]．