例析两最值函数的应用
甘肃省陇西县第一中学 (748100) 王耀文
高二一次月考中,有一个填空题难住了绝大多数学生,命题者给出的参考答案也很复杂,我给学生认真分析此题后,认为此题应该考查函数max{f(x),g(x)},教材选修4-5中出现过此类函数,通过分析学生并不陌生,事实上2015年全国Ⅰ卷理科、浙江卷理科也出现过此类问题,特别是由于浙江、上海率先进行新一轮高考改革,他们每年的高考试题备受广大师生的关注.因此笔者想通过一些考题简单分析max{f(x),g(x)}和min{f(x),g(x)},以飨读者,不足之处,敬请指正.
1.考题呈现
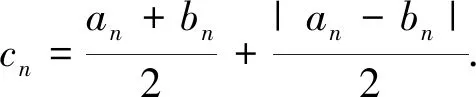
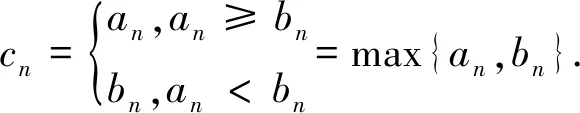
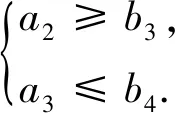
2.链接高考
例1 (2015年浙江理科高考第18题)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值.
(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值.
简析:(1)当|a|≥2时,f(x)在[-1,1]上单调,∴M(a,b)=max{f(-1),f(1)}.显然:M(a,b)≥|f(-1)|且M(a,b)≥|f(1)|.即M(a,b)≥|1-a+b|且M(a,b)≥|1+a+b|.所以
2M(a,b)≥|1-a+b|+|1+a+b|≥|(1-a+b)-(1+a+b)|=2|a|≥4,故M(a,b)≥2.
(2)略.
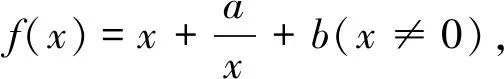
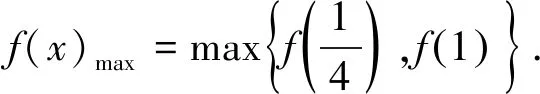
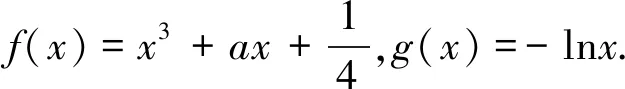
(1)当a为何值时,x轴为曲线y=f(x)的切线;
(2)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),讨论h(x)零点的个数.
简析:(1)略;
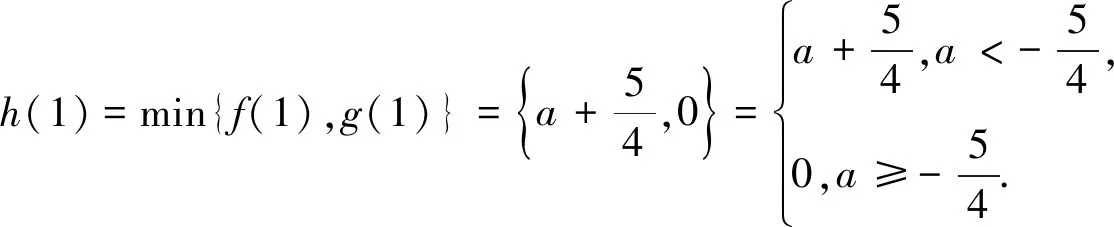
3.链接教材
例4 已知a>0,b>0,且h=
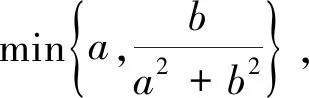
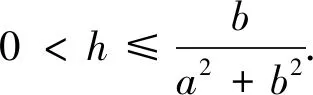
4.链接竞赛
例5 对于每一个实数x,设f(x)是y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,则f(x)的最大值为.
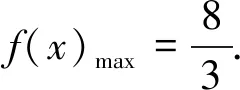
例6 (2018年全国高中数学联赛河南省预赛第5题)已知a,b,c均为正数,则
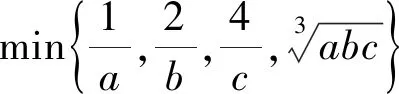
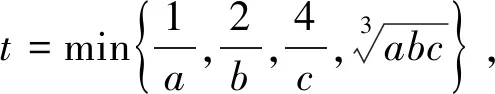
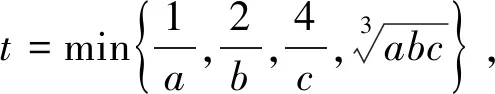
5.归纳总结
3.max{f(x),g(x)}≥f(x),且max{f(x),g(x)}≥g(x).
4.min{f(x),g(x)}≤f(x),且min{f(x),g(x)}≤g(x).
教师是落实核心素养教育体系的执行者,课堂教学是培育学科核心素养的主阵地,教材知识是提升核心素养的重要源泉.很多高考试题包括竞赛题都源于教材,因此我们教师要深入研究教材,充分发挥教材的作用.

