论教材习题教学在发展学生核心素养的作用*
福建省邵武第一中学 (354000) 郭胜光
高中数学习题课的教学中如何发展学生数学核心素养,是值得研究的课题.笔者认为,核心素养导向下的习题课的教学要关注教材习题,发挥教材习题教学在发展学生核心素养的作用.然而,高中数学教学忽视教材习题的作用,处处可见.众多高中学生和相当一部分高中数学教师不重视教材习题研究,从而,错误认为教材的习题太简单,做教材习题无法应对高考,而把课外教辅材料当做解题宝典.这种本末倒置的认识是非常可悲的,其造成的后果是学生机械重复做了大量的习题(“题海战术”),而数学能力并没有提高,导致绝大部分学生厌恶数学,高考数学也不可能取得好成绩,更谈不上学生核心素养的发展.
尽管相关要求都在强调“回归课本”,但不少教师置若罔闻.笔者经过长期调研发现,很多教师不是不重视教材习题研究,而是不懂得挖掘教材习题内涵和隐藏的数学思想和方法;不懂得将教材习题改造、引申、推广得到有价值的结论;不懂得众多高考试题源于教材,根植于教材之中;不懂得教材习题教学在发展学生核心素养的作用.因此,要使广大数学教师认识教材习题的重要性,必须引导教师从以下几个方面研究教材的习题.
1.研究一题多解,发展学生“数学运算”素养
对于教材习题的学习,学生常常只关注会不会解这一道题,很少关注习题所隐藏的数学思想方法.众所周知,数学习题可以千变万化,但其隐藏的数学思想方法是永恒的,领悟了数学思想方法,就抓住解决数学问题的金钥匙,做到以不变应万变.教学实践表明,对教材中经典习题一题多解的研究,引导学生挖掘问题的多向性和解决问题的多样化,既能提高学生学习数学的兴趣,又是发展学生“数学运算”素养的重要途径.
案例1 (苏教版高中数学选修4-5第17页例7)已知x>0,y>0,z>0,证明:x3+y3+z3≥3xyz.

点评:该证法是教材中所给的证法,属于传统的比差法.即作差→变形→定号.这种证法思路简单,但因式分解要求较高,其结果是学生有思路但不易成功.



点评:导数法的本质就是构造函数g(x)=x3-3yzx+y3+z3,将证明不等式问题转化为证明函数g(x)的最小值不小于零,而利用导数求三次函数最值的方法属于通性通法,学生没有困难都能完成.该证法思维含量高,体现了化归转化的数学思想和函数思想.
2.研究一题多变,发展学生“逻辑推理”素养
一题多变,变的是形式,不变的是本质.平时教学中,教师要善于利用教材中的精典习题,引导学生探究一题多变,给学生足够的创造空间,充分发挥学生的主体作用,激励学生去思考,激发学生的创新意识,从而发展学生“逻辑推理”素养.
案例2 (人教A版高中数学选修2—1第73页习题A组第6题)O为坐标原点,若直线y=x-2与抛物线y2=2x相交于A,B两点,求证OA⊥OB.

变式1O为坐标原点,若直线y=k(x-2)与抛物线y2=2x相交于A,B两点,问OA与OB是否垂直?
分析:设A(x1,y1),B(x2,y2),由

变式2O是坐标原点,若过点M(2p,0)(p>0)的直线与抛物线y2=2px相交于A,B两点,问OA与OB是否垂直?

变式3O是坐标原点,直线AB与抛物线y2=2px(p>0)相交于A,B两点,若OA⊥OB,直线AB是否过定点?
分析:设A(x1,y1),B(x2,y2),直线AB方程为x=ty+m.

由学生归纳得到定理:O是坐标原点,直线AB与抛物线y2=2px(p>0)相交于A,B两点,则OA⊥OB的充要条件是直线AB过定点M(2p,0).
通过对习题的条件的变化以及条件和结论的互换,逐步引导学生探究问题的本质,最后由学生得到课本没有的新定理,从而培养学生发散性思维.研究资料表明:学生创新意识与他的发散性思维成正比.
3.研究习题的推广,发展学生“数学抽象”素养
学好数学的有效方法是“再创造”,在日常的教学中,教师要积极引导学生研究教材经典习题推广,由学生去发现或创造出新的结论,寻找更一般的规律.长期坚持,能激发学生学习兴趣,促使学生形成积极主动、勇于探索的学习方式.教学实践表明,研究习题的推广是发展学生“数学抽象”素养的有效途径.





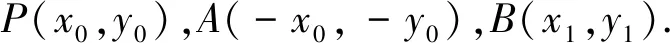
对于选择题和填空题,我们所得到的“结论和方法”可以直接使用,对于解答题,不宜直接使用,而应把定理推导重写一遍,既使这样也比常规方法简单的多.教学实践证明,对教材中一些典型例题和习题的结论进行推广,既可以培养学生的探究能力,提高学生思维起点,又可以提高学生高考数学成绩.
笔者的多年教学实践表明,对教材习题研究是一个不可忽视的问题,发挥教材习题的重要作用,引导学生回归课本,使数学概念和习题教学落到实处,这才是高中数学教学的“正道”.

