一节公开课的实践和思考
江苏省扬州中学 (225009) 戚有建江苏省扬州市新华中学 (225009) 王梅蓉
提到公开课,多数教师都是怕上、不愿意上,因为不仅要花大量时间去准备,而且上完课后还可能会被议论被批判,所以遇到上公开课时,多数教师都是能躲则躲、能不上就不上.笔者就此有新的看法,虽然上公开课会有压力、会很辛苦,但是咬咬牙也就过来了,关键是上完公开课后你会有很多想法和感受,因为整个过程是你精心准备、仔细推敲、亲身经历的,所以肯定会有很多感受和体会,可以进行教学反思,通过反省自己的教学思想、教学行为,可以快速的提升自我.叶圣陶说的好:“一个教师写一辈子教案、教一辈子书不一定能成为优秀教师,但如果能坚持写三年的教学反思,就很可能会成为优秀教师”.前不久,江苏省沛县数学教师来我校交流,笔者主动请缨为他们上了一节公开课,课题是“不等式恒成立,求参数范围”,面向学生是我校高一年级重点班学生,下面是本人这次公开课的教学过程和教学感想.
一、问题引入
问题1 若对任意x∈[2,3],不等式x2+ax-a<0恒成立,求实数a的取值范围.
设计意图:问题是思维的载体、是思维的动力,数学教学要以问题为中心,数学课要从问题开始,本节课就是从学生熟悉的二次函数入手,启迪学生思考.
二、解法研究
点评:解法1是将不等式恒成立转化为二次函数最值问题,通俗易懂,学生容易想到,由于参数a影响抛物线的对称轴,所以要分情况讨论处理.本题通常分四种情况,这是最基本的处理方法,在此基础上,可启发学生能否少讨论?学生经过思考讨论后会发现最大值一定是f(2)、f(3)中的某一个,所以就不难想到下面的解法2、解法3.

解法3:(转化为研究二次函数最大值,不需要讨论处理)令f(x)=x2+ax-a,x∈[2,3],则

点评:解法1、解法2、解法3都是将不等式恒成立转化为二次函数最值问题来处理,但是在处理讨论问题上却反映了不同的思维水平,此外,我们也可以将参数a分离出来处理,得到解法4.

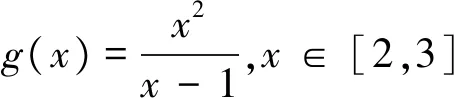
另外,在研究完各种解法后可以让学生进行比较,即用二次函数处理与用分离参数处理各有什么优势,各有什么不足.
三、类比研究
问题2 若存在x∈[2,3],不等式x2+ax-a<0成立,求实数a的取值范围.
答案:a<-4.
设计意图:设计形同质异的问题,将“任意”改成“存在”,让学生在比较、辨析中体会虽然问题的形式一样,但是问题的本质却不一样,从而加深学生思维的深刻性.
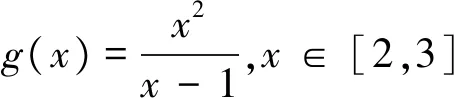
四、变式研究
问题3若函数f(x)=lg(a-ax-x2)在x∈[2,3]上有意义,求实数a的取值范围.
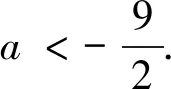
问题4 已知集合A=[2,3],B={x|x2+ax-a<0},若A∩B=A,求实数a的取值范围.
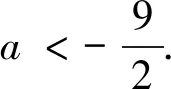
问题5 已知集合A=[2,3],B={x|x2+ax-a<0},若A∩B≠∅,求实数a的取值范围.
答案:a<-4.
设计意图:设计形异质同的问题,让学生在比较、辨析中体会虽然问题的形式不一样,但是问题的本质却一样,也就是“多题一解”“多题归一”,从而避免陷入题海,这种设计可以加深学生思维的深刻性.
点评:问题3、问题4可以转化为问题1,问题5可以转化为问题2.
五、巩固提升

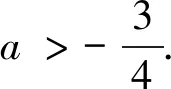

六、教学反思
1.问题是思维的动力
问题是思维的载体、是思维的动力,一个有价值的问题是数学课成功的前提.这个问题要具有以下特征:①问题要有一定的知识容量,涉及到的知识面要宽、思想方法要多;②问题要具有层次性,可供不同水平学生作不同层次的探究;③问题要具有开放性,探究的过程和结果丰富多彩;④问题要具有沿展性,可供学生发现新问题作进一步的探究.波利亚也说过“一个好的教师能够拿出一个有意义的题目,去帮助学生发掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域”.
2.学生是学习的主体
教学方式的转变是新课程改革的最本质要求,新课程强调,教师要更新教育观念,改变教学方式,让学生由被动学习转变为主动学习,教师要由原来的知识传授者转变为学生学习的组织者、引导者、合作者与共同探究者,要让学生从原来的被动接受者转变为主动探究者,体验到了探究的乐趣,体验到了成功的乐趣.问题要尽量让学生自己去发现、让学生自己提出,方法要尽量让学生自己去想,去尝试、去比较,总结要尽量让学生自己去感悟、去归纳,变式题要尽量让学生自己去变、去编.
3.放手让学生去体验(成功和失败)


