多矢量定姿的SVD和QUEST算法等价性分析

严恭敏，陈若彤，郭 鹍

（1.西北工业大学 自动化学院，西安 710072；2.中船航海科技有限责任公司，北京 100070）

捷联惯导系统初始对准的重点在于初始姿态阵的求解，它通常可分为滤波估计和确定性算法两种方法[1]。滤波方法通过建立系统误差模型，模型中往往包含了惯性传感器误差，在系统建模准确的情况下一般具有较好的对准精度。然而，滤波方法通常只有在小失准角误差线性建模条件下才会比较有效，虽然大失准模型及其非线性滤波方法研究较多，但实际工程使用的却比较少。采用大失准角模型通常也只是为了获得粗略的失准角，再转而使用小失准角线性模型，才能得到高精度的初始对准结果[2]。

确定性姿态算法与模型是否线性无关，在航天器姿态确定中应用较多，它同样也适用于捷联惯导的粗对准过程，有时在惯导机动干扰不大的场合也能获得较高的初始对准精度，甚至达到精对准的效果[3-4]。姿态确定算法早期研究主要源于解决卫星姿态的确定问题。1964年Harold Black提出了利用两组观测矢量求取姿态转换矩阵的代数方法TRIAD（Tri-Axial Attitude Determination，常称为双矢量定姿法）；1965年Grace Wahba提出了应用观测矢量进行星体姿态确定的最小二乘优化问题（常称为 Wahba问题）[5]；1968年Davenport提出了q-method方法，采用四元数姿态描述方式解决 Wahba问题，或称 QUEST估计方法（QUaternion ESTimator）[6]。由于早期计算机的运算能力有限，研究者们提出了一系列改进的四元数优化快速算法，比如FOAM（Fast Optimal Attitude Matrix）、ESOQ（EStimator of the Optimal Quaternion）、ESOQ2（Second ESOQ）等算法，主要用于降低计算量和提高数值鲁棒性[7-10]。研究者普遍认为，与姿态的矩阵优化相比，四元数优化具有更少的约束，因而研究工作主要围绕四元数展开。实际上，Wahba问题的四元数优化与矩阵优化是完全等价的，前者相对于后者并不具有丝毫的姿态求解精度优势，反而是四元数及其快速算法更加烦琐，快速算法的计算量降低程度对现代计算机而言几乎可忽略不计。

本文简要介绍了姿态矩阵的奇异值分解优化与四元数特征向量求解优化之间的等价性，在四元数优化过程中提出了一种新的构造四阶矩阵的方法；为了增强姿态阵优化算法的实用性，给出了一种快速奇异值分解优化算法，其浮点乘法计算量与四元数优化快速算法 ESOQ2相近；最后，对几种算法之间的等价性进行了仿真验证。

1 定姿算法理论分析

1.1 问题描述

假设三维空间中有m(m＞2)个不共面的矢量Vi（i= 1,2,,m），在直角坐标系b系和r系中同时对这些矢量进行测量，结果分别记为和，由于存在测量误差，它们只能近似满足如下变换关系：

为了定量描述“最优”性能，这里构造指标函数为

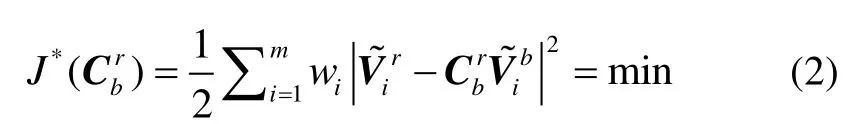
1.2 三阶矩阵的SVD方法

对式(2)中的误差平方进行如下等价变形：

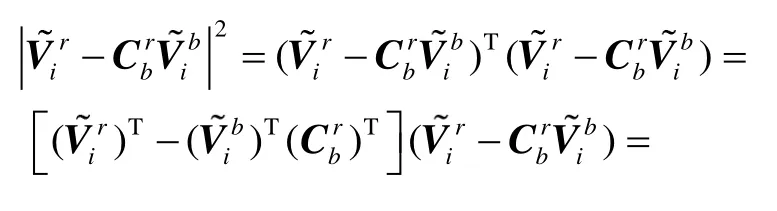
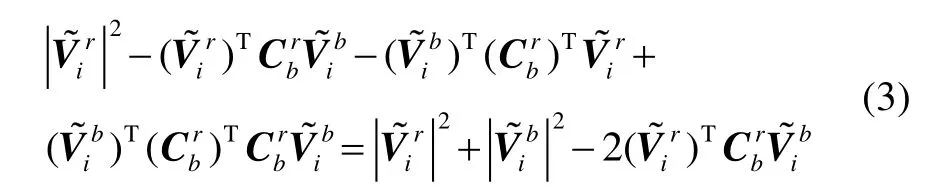
将式(3)代入式(2)，得：

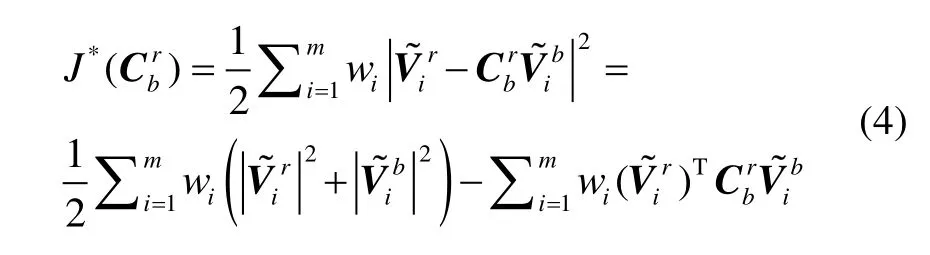
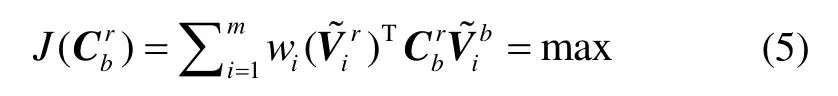
进一步对式(5)作变换，可得：

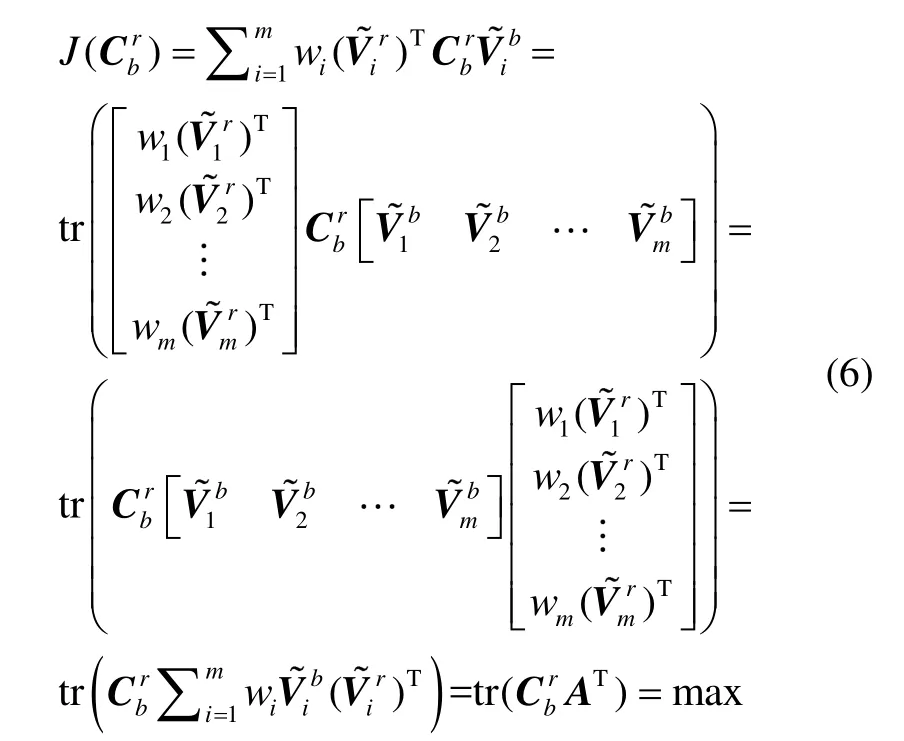
其中，记

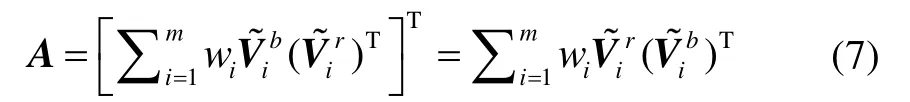
假设矩阵A可逆且其奇异值分解为A=UDVT，则式(6)可变为

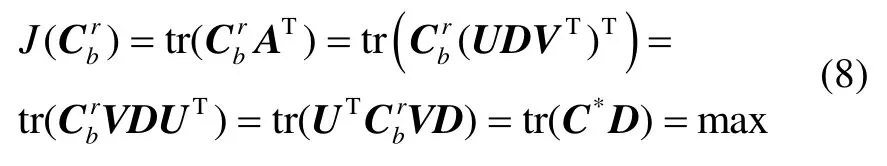
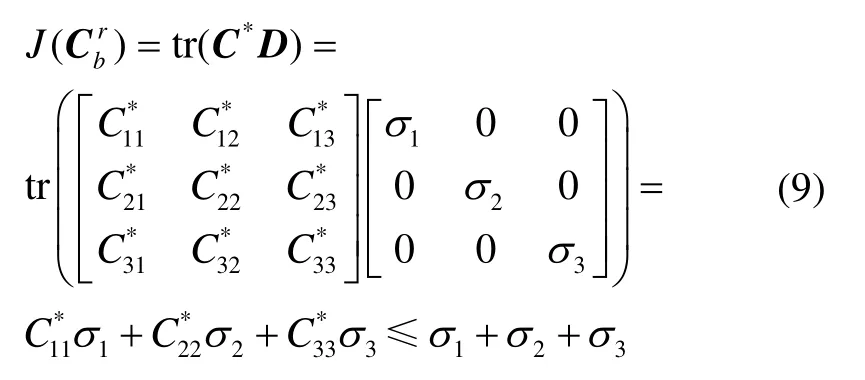
由于奇异值σ1≥σ2≥σ3＞ 0（如果有奇异值近似等于零则需特别讨论，文中暂不涉及），所以在式(9)中最后等号当且仅当时成立，这正好对应于C*=I。根据可求得最优姿态矩阵：

1.3 四阶矩阵的特征向量方法

① QUEST方法1

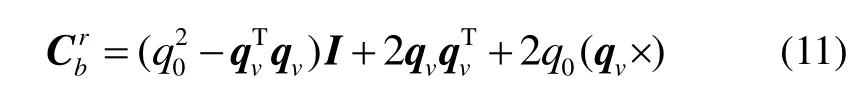
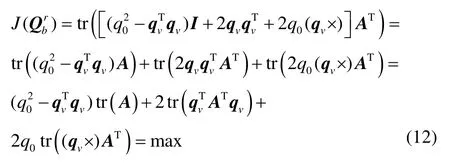
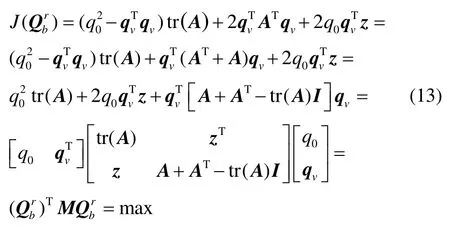
其中，记

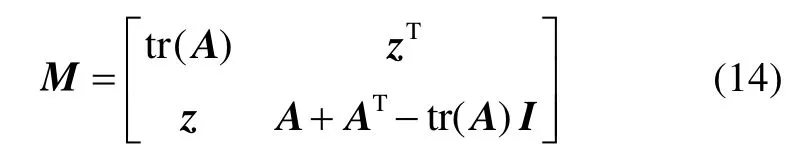
显然，矩阵M为四阶实对称阵，其特征值均为实数且特征向量均为实向量。

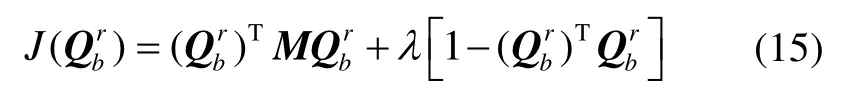
对式(15)求导并令其等于零，可得：

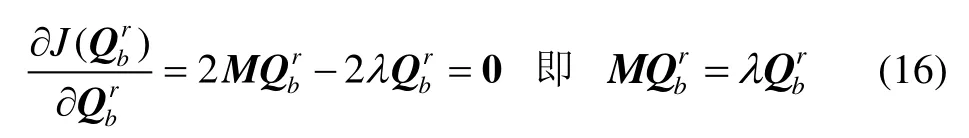
这说明λ是矩阵M的特征值，是相应的特征向量。将式(16)代入式(13)，可得：

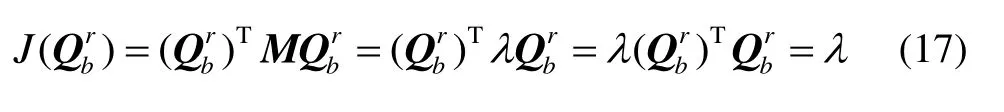
从前述分析可知，必然有极大值等式λmax=σ1+σ2+σ3成立，这说明SVD姿态阵方法与特征向量四元数方法得到的结果是等价的。

② QUEST方法2

若将三维向量视为零标量四元数，则式(5)可化为

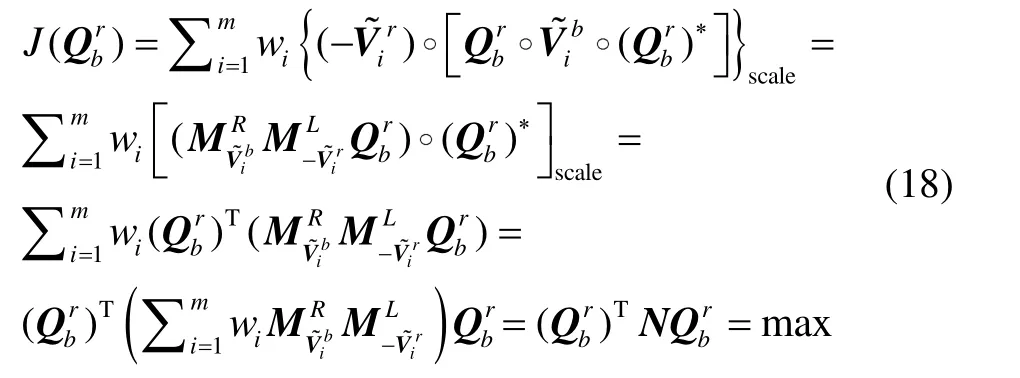
比较式(13)和式(18)，发现它们在形式上完全一致，若记和i=A直接采用元素展开法可以验证式(19)成立：

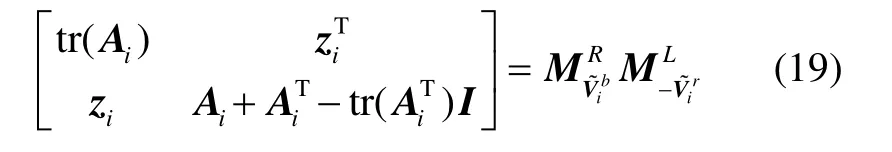
从而容易证明有M=N，当然获得M的运算量会略小些，但是计算N的过程更直观些。因此，四阶实对称矩阵N的最大特征值λmax所对应的单位特征向量即为所求的四元数

③ QUEST方法3

直接将式(2)中的误差平方改写成四元数的形式，为

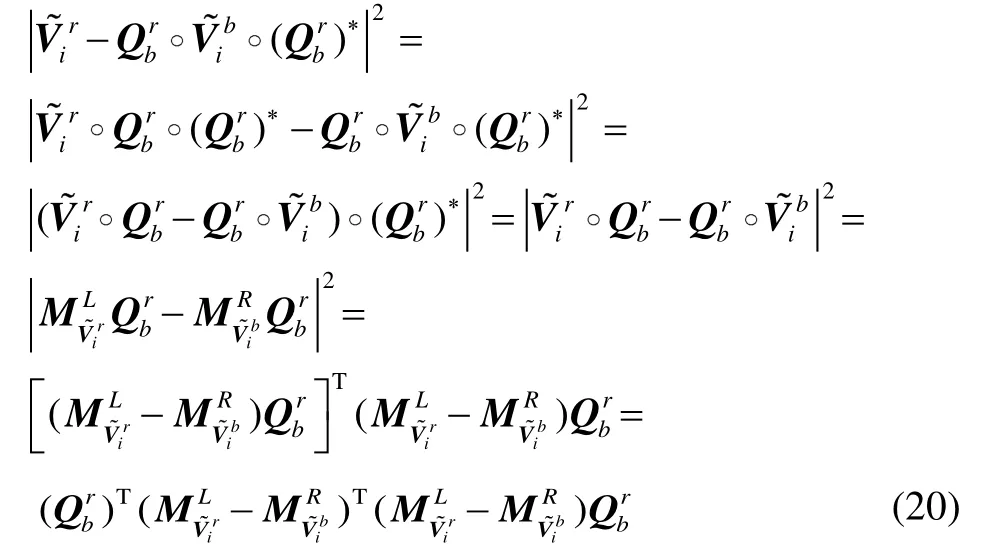
将式(20)代入式(2)，可得指标函数：

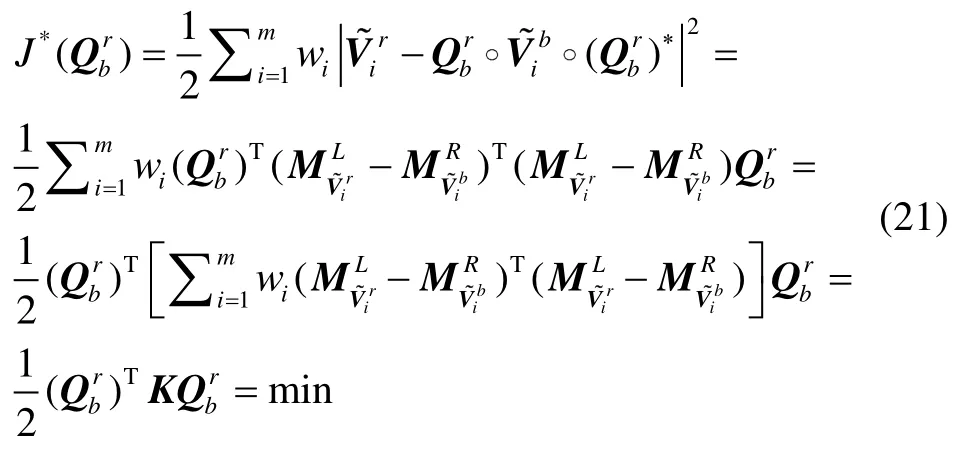
2 快速奇异值分解算法（FSVD）

对于式(7)，当A可逆时B=ATA必定是对称正定阵，求解矩阵B=(Bij)的特征多项式为

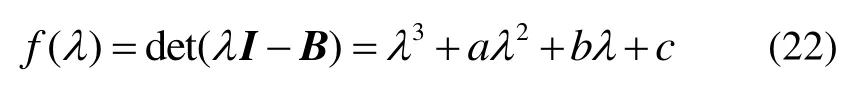
其中，

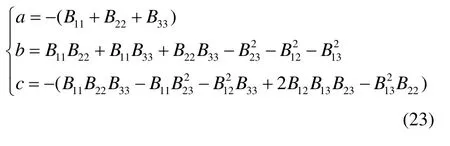
由于实对称阵的特征值均为实数，根据三次方程的求根公式可直接求得f(λ) = 0的三个根，分别为

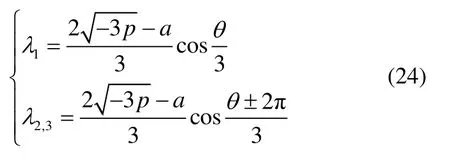
其中，

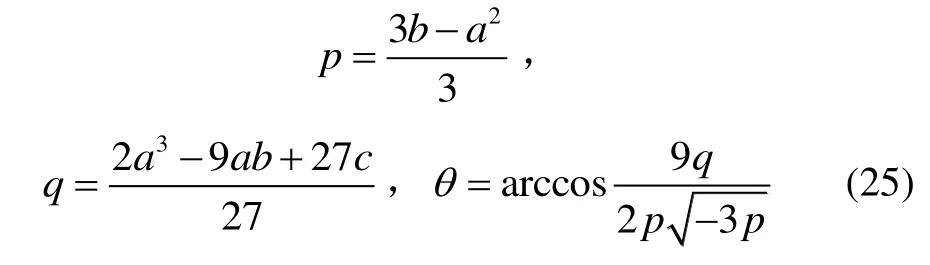
实对称矩阵存在完备的正交特征向量系，即存在两两正交的特征向量，利用这一性质有助于简化B的特征向量求解过程。假设特征值经过排序后有λ1≥λ2≥λ3＞0，以下按照特征值重复情况求解特征向量。

① 当有三重特征值时，即λ1=λ2=λ3，则可直接构造三个特征向量：

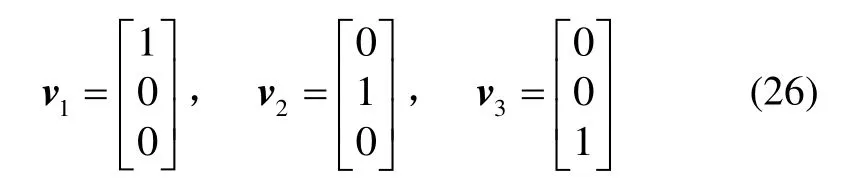
记C=λ2I-B，则有rank(C)=1，这说明C的三个行向量之间是线性相关的。在矩阵C中寻找绝对值最大的元素（理论上可以是任意不为0的元素），假设为Cij，则有：

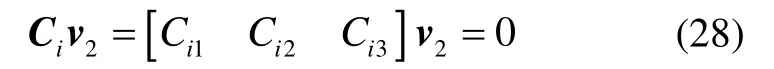
其中，Ci表示矩阵C的第i行向量，而为矩阵C的第i行j列元素。

如果j=1或j=2，可直接构造如下特征向量：

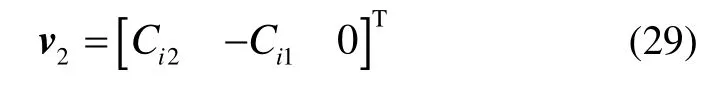
而如果j=3，则直接构造如下特征向量：

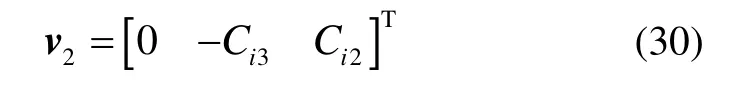
当λ1=λ2＞λ3时，使用如下方式构造特征向量v1和v3：

而当λ1＞λ2=λ3时，使用如下方式构造特征向量v3和v1：

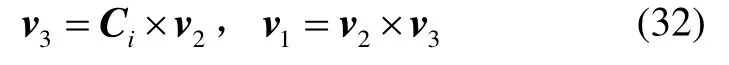
③ 当有三个互异特征值时，与λ1对应特征向量v1满足如下方程：

同样，若记C=λ1I-B，则有rank(C)=2，这说明C的三个行向量应在同一平面上（规定零向量可在任意平面上），且至少有两个是不相互平行的，计算如下三组行向量的叉乘：

理论上vt1、vt2、vt3三者相互平行，只要不是零向量均可作为特征向量，但在数值上可选取模值最大者，作为λ1对应的特征向量v1。

对于特征向量v2求法类似于v1，而针对特征向量v3，可选择v3=v1×v2。

最后，将特征向量v1、v2、v3做规范化处理，令

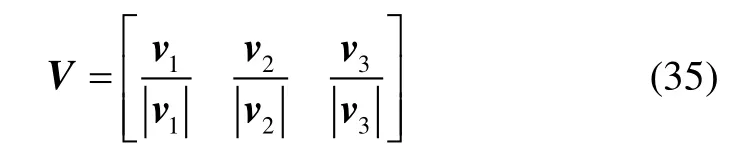
则有矩阵B的特征值和特征向量分解：

其中，Λ=diag(λ1λ2λ3)，且显然V为单位正交阵。

由奇异值分解式UΛ1/2VT=A两边同时右乘VΛ-1/2VT，直接得最优单位正交阵：

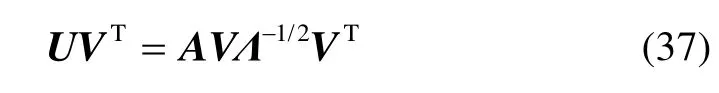
FSVD算法的浮点乘法计算量分析：三次方程求根式(23)～(25)中约30次；计算特征向量过程中，以情况③最为复杂，约需50次；计算最优单位正交阵式(37)约需60次。因此，总计乘法约140次。当然，在式(24)(25)(35)(37)中还需要2次三角函数、1次反三角函数和7次开方运算。

3 仿真验证

本节从仿真的角度对前述理论分析进行验证，设计如下仿真步骤：

② 生成m=100个随机测量向量误差向量和加权因子，其中，

④ 分别采用 SVD、FSVD、QUEST1、QUEST2和QUEST3五种算法求解最优姿态矩阵或四元数，除FSVD采用第 2节所提方法外，其它算法直接调用了Matlab的svd()和eig()函数；

⑤ 以SVD算法作为参考基准，计算其它四种算法相对于SVD算法的失准角误差的模值；

从图1可以看出，SVD和三种QUEST算法之间的误差均很小，仅为10-15rad量级，该误差主要由计算机的数值计算精度引起，这在实际应用中完全可忽略不计。由于计算矩阵时进行了平方运算，使得 FSVD的误差约大一个数量级，在矩阵条件数很大的情况下计算机数值求解误差可能会比较大。至此，通过仿真验证，可以认为SVD、FSVD、QUEST1、QUEST2和QUEST3五种多矢量定姿算法是相互等价的。

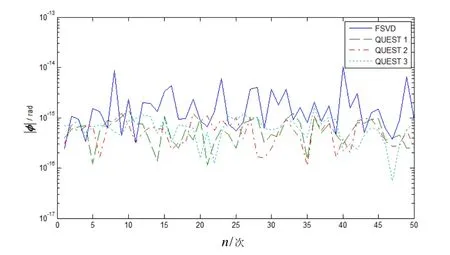
图1 各种算法之间的误差Fig.1 Error comparisons for the five algorithms

4 结 论

针对姿态确定的Wahba问题，证明了姿态矩阵的奇异值分解算法与三种四元数特征向量求解算法之间的等价性，给出了一种快速奇异值分解算法，对几种算法进行了仿真验证。理论分析和仿真实验表明，对于当前计算机的运算能力而言，各种算法之间的数值计算精度和计算量并无显著差别，均可满足实际应用要求。建议今后大家在撰写论文时，特别是在基于惯性系的初始对准相关论文中，直接采用姿态阵进行表示并用奇异值分解方法进行求解即可，这样更加简洁和直观，而没必要采用更复杂和不易理解的四元数描述，看似提升了论文的理论水平，其实两者的本质和结果是完全等效的[11-12]。