一种基于Haar小波的光纤陀螺信号实时滤波方法

曲俊海，夏元清，李 静，王海稳

（1.北京理工大学 自动化学院，北京 100081；2.北方自动控制技术研究所，太原 030006；3.太原科技大学 电子信息工程学院，太原 030024）

惯性稳定平台控制系统多以光纤陀螺作为敏感相对惯性空间旋转角速度的测量元件，利用反方向补偿该角速率的变化，实时闭环控制实现稳定及跟踪功能[1]。但是，光纤陀螺输出的角速度信号中含有噪声，该输出噪声会直接影响到惯性稳定平台的控制精度。尤其当处于低速工况时，未经滤波处理的陀螺输出噪声分量的标准偏差值甚至高于陀螺的期望输出值，系统输出除了跟随输入信号外，还要跟随陀螺的输出噪声，控制效果受噪声影响很大。因此，光纤陀螺的性能是影响系统控制精度的关键因素。

针对提升陀螺信号质量的问题，国内外学者提出的软件滤波方法主要分为三种：

一是利用卡尔曼滤波对陀螺信号进行滤波[3-4]。这类滤波方法在随机噪声模型建立准确的情况下，具有较好的滤波效果，然而在实际应用中很难得到准确的模型，因此滤波效果往往受到模型精确性的较大限制。二是平滑滤波，例如滑动平均，最小二乘回归或者Savitzky-Golay回归等[5-6]。这类方法不依赖于先验知识，而且运算量小，适合在线进行，然而此类方法的鲁棒性较差，当陀螺信号出现有用的突变信号或者异常的野值时，滤波效果会受到很大影响。

三是变换域滤波，该类方法通常根据有用信号和噪声的频率分布特性[7]，设计相应的低通或带阻滤波器对噪声进行滤除，此类方法由于实现简单且效果明显，曾在工程上被广泛应用。

然而事实上，光纤陀螺的噪声分布于各个频带，频域滤波法无法彻底滤除低频噪声或表征信号的突变点。小波变换是一种在时-频方面都具有表征信号局部特征能力的方法，利用正交小波的多分辨率特性对信号进行处理，相当于多个带宽不同的滤波器对信号进行处理，根据信号和噪声的不同特征，将其区分开来。

目前已有文献[8-10]利用小波方法对陀螺信号进行滤波，多为基于Daubechies小波基的阈值小波去噪方法。这类小波去噪方法又大可分为两类：一类是事后滤波方法，即将所有陀螺数据一次性作为输入，整体得到滤波后的值，此类方法不能满足实时性应用需求；另一类是滑动窗滤波方法，设置一定长度的滑动窗，以最新一段陀螺数据为输入，或者对滑动窗截取的最新一段陀螺数据进行一定方法的扩充，让当前时刻信号采样值位于待滤波数据的非边缘段，以此作为滤波输入数据，得到滤波数据后取对应时刻的输出，此类方法确可满足实时滤波需求，但精度较差。因此，提出了对光纤陀螺输出信号进行小波实时滤波的技术需求。

本文在进行大量仿真实验的基础上，说明了影响现有小波方法实时滤波效果的根源，即边界问题；进而从理论出发，对边界问题产生的原因进行深入剖析，得出其源于对支撑集的要求，在指出Harr小波基的支撑集符合要求后，进一步证明了Harr小波基可实现连续阶梯信号的逼近；最后提出一种基于Haar小波的实时光纤陀螺信号滤波方法。该方法既利用了小波优越的信号-噪声分离能力，又可满足实时应用背景的要求，有效地实现了光纤陀螺信号噪声的实时滤除。

1 基于小波理论的去噪方法

小波阈值方法由 Donoho提出，该方法认为信号对应的小波系数包含信号的重要信息，其幅值较大，但数目较少，而噪声对应的小波系数是一致分布的，个数较多，但幅值小。阈值法由于实现简单、计算量小，在工程中得到了广泛的应用。

利用小波阈值法去噪一般分为3个步骤：

① 对信号进行小波分解，得到各尺度下的小波系数，以三层分解为例，小波分解结构如图1所示，cn表示第n层的近似小波系数（也称低频系数），dn表示第n层的细节小波系数（也称为高频系数）；

② 根据噪声能量及分布为每个尺度的小波系数选择合适的阈值，对细节小波系数进行阈值操作得到新的小波系数组合；

③ 由新的小波系数进行重构得到去噪后的信号。

图1 小波分解示意图Fig.1 Diagram of wavelet decomposition

2 基于Daubechies基的小波滤波

2.1 边界问题

小波分解和重构是小波去噪的关键环节，工程中多使用 Daubechies小波基（简称为 DbN小波基，N为小波的阶数）来实现小波分解与重构。

实际工程中的小波滤波过程的实现都依赖于Mallat塔式多分辨分解与重构算法，该算法实现一次小波分解的过程如图2所示。图中：()s k为原信号；在基于 Daubechies基的小波滤波中，()h k、 ()g k是Daubechies小波基的分解低通滤波器和分解高通滤波器，原信号通过与分解低通和分解高通卷积得到低频系数和高频系数； ()c k和 ()d k分别为分解后的低频系数和高频系数；()c k′和()d k′为经过下采样后的低频和高频系数。

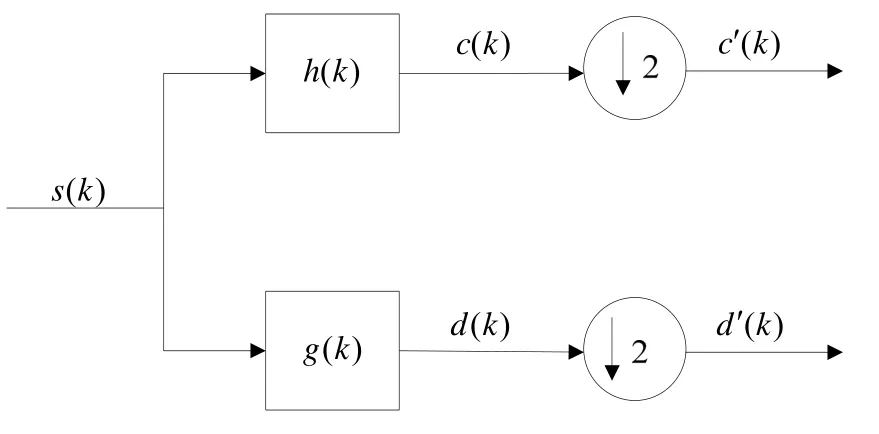
图2 Mallat算法一次小波分解实现过程Fig.2 Process of one layer wavelet decomposition in Mallat

Mallat算法实现一次小波重构的过程如图3所示。

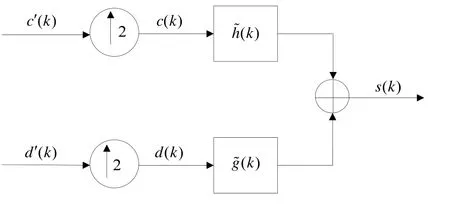
图3 Mallat算法一次小波重构实现过程Fig.3 Process of one layer wavelet reconstruction in Mallat

Mallat算法是在假定原始信号无限长的基础上进行的，但实际工程中，我们通常都是对有限长信号进行滤波。

设s(k)为原始信号的L个离散值（1 ≤k≤L），h(k)、g(k)分别为分解低通滤波器和分解高通滤波器，其长度为M。原始信号分别与分解低通滤波器、分解高通滤波器进行卷积得到近似小波系数c(k)和细节小波系数d(k)，见式(1)和式(2)。

可以看到，当计算c(1),…,c(M-1)和d(1),…,d(M- 1)时，需要原信号s(k)初始时刻之前的值参与运算，即左端越界；当计算c(L+ 1),…,c(L+M-1)和d(L+ 1),…,d(L+M-1)时，需要原信号s(k)在L时刻之后的值参与运算，即右端越界。

重构过程卷积运算表达式参见式(3)，可以看到，重构过程也面临数据越界现象。

2.2 边界问题对实时滤波性能影响分析

从上述小波分解与重构的过程中可以看出，基于Daubechies基的小波滤波实现过程中，存在数据越界现象，因此实现步骤中包含边界延拓。

延拓方法主要有零延拓、周期延拓、对称延拓三种，其具体实现方式为：

① 零延拓

原信号：s(1),s(2),…,s(k)

延拓后信号：0,…,0,s(1),s(2),…,s(k),0,…,0

② 对称延拓

原信号：s(1),s(2),…,s(k)

延拓后信号：

…,s(3),s(2),s(1),s(1),s(2),

…,s(k),s(k),s(k- 1),s(k-2),…

③ 周期延拓

原信号：s(1),s(2),…,s(k)

延拓后信号：

…,s(k- 2),s(k-1),s(k),s(1),s(2),

…,s(k),s(1),s(2),s(3),…

为考察边界延拓方法对数据越界问题的效果，进行了仿真实验。仿真对象采用信号s=sin(0.2πt)，原信号取 10个采样点，采样序列为{0.31038,0.00159,-0.30735,-0.58624,-0.80779,-0.95037,-0.99999,-0.951 84,-0.810 61,-0.590 10}。根据已有试验经验，在对陀螺信号滤波时，Db3小波基往往优于其他Dbn（n≠1）小波基，故本文中所有试验均选用Db3小波。由于信号分解出的低频系数决定了信号的基本轮廓，所以只对采用几种延拓方法所得到的一级分解低频系数进行分析，并与使用真实正弦信号延拓后所得到的低频系数进行对比。仿真结果如表1所示。

表1 低频系数对比结果Tab.1 Comparison on low frequency coefficients

从表1中可以看出，与使用真实信号延拓相比，其他无论何种延拓方式，中间的低频系数（系数 3、系数4、系数5）相同，两边的低频系数（系数1、系数2、系数6、系数7）都出现了偏差。

为更直观地说明边界问题的影响，模拟生成10 (°)/s的速度信号，并加入高斯白噪声作为陀螺仿真原信号，在所有原信号生成后，将其作为输入进行一次性整体滤波（本文称为离线滤波），使用Db3对输入信号进行阈值去噪，延拓方法为零延拓，滤波效果如图4所示。

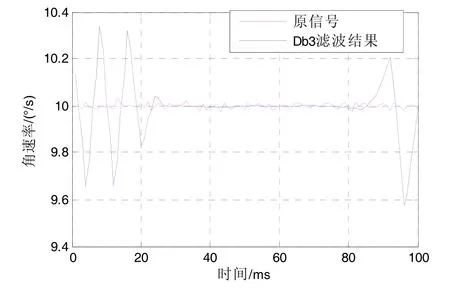
图4 基于Db3小波的离线滤波结果Fig.4 Offline filtered result based on Db3

从图4中可以看到，边界问题对原信号左边界和右边界的滤波结果都产生了较大的影响，使得滤波值的准确度明显变低。而在实时小波滤波时，我们获取的当前时刻信号正位于待滤波信号段的最右端，其滤波结果的准确度取决于右边界滤波结果的准确度，因此，在使用Daubechies小波基时，克服边界问题对实时光纤陀螺滤波至关重要。

3 基于Haar小波的实时陀螺信号滤波方法

3.1 Harr小波适用性分析与证明

由第2节可知，当采用Db3小波进行光纤陀螺滤波时，在数据边界滤波结果的准确度将大为降低，而在实时控制系统中，用于闭环运算的数据正是当前的实时数据（即在边界的数据），因此边界问题处理不好会对系统控制产生不利的影响。分析引起此问题的原因是由于塔式分解计算的过程中需要用到采样点以外的数据，而在实际系统中无法准确预知未来的数据。为克服边界问题，从小波理论出发，进一步分析可得到引发此问题的原因。由图5(a) Db3小波尺度函数图可以看出，Db3小波函数的支撑区间为0 ≤t≤ 5，因此当进行下一层分解时其支撑区间为0 ≤t≤ 2.5，需要6个系数才能运算得到，如图5(b)所示。

而按照塔式分解的方法，在边界分解时超过2个小波系数就需要用到原信号的未来数据了。因此带来了边界问题。

图5 (a) Db3小波尺度函数图Fig.5 (a) Wavelet scale function of Db3

图5 (b) 第一层分解的小波尺度函数Fig.5 (b) Wavelet scale function when doing first layer decomposition

解决此问题的根本方法是使小波函数的支撑集不大于1，即0 ≤t≤ 1，而按照Db小波的构造办法可知，只有Db1即Harr小波的支撑集可限制在0 ≤t≤1的范围内。但 Harr小波缺点是逼近连续信号的能力差，因此还需要证明Harr小波用于光纤陀螺滤波的适用性问题。

本文研究的对象是光纤陀螺信号，实际工程中，都是以一定时间间隔对光纤陀螺信号进行数据录取。某静置光纤陀螺输出信号如图6(a)所示，对采样区间[9,10]的陀螺信号进行局部放大，得到图6(b)。可以看到，待处理的光纤陀螺信号是连续阶梯信号。

图6 (a) 某光纤陀螺输出信号Fig.6 (a) Original signal of FOG

图6 (b) 陀螺信号局部放大图Fig.6 (b) Partial amplification of the original signal

小波分解时，首先要确定近似空间Vj，使其能最佳地反映原信号s的各种信息，然后选择sj∈Vj，最佳地逼近s。由于 2j/2φ(2jx-k)是Vj空间的标准正交基，因此s在Vj上的投影Pj s可表示为：

其中，

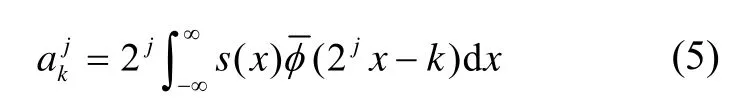
定理：若 {Vj,j∈Z}是一个依紧支撑尺度函数φ的多分辨率分析，如果s∈L（2R）是如图5(a)所示的连续阶梯函数，那么当选择j，满足2j=N时（N为信号长度），当φ满足以下条件：

ⅱ）φ支撑集为[0,1]，可得式(1)中，

对上述定理展开证明，φ是紧支撑的，其非零集被限定在一闭包[0,1]中，因此等式中x的积分区间是0 ≤ 2jx-k≤ 1。进行变量替换t= 2jx-k，可得：

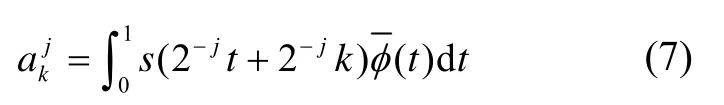
如图6(b)所示有s(2-jt+ 2-jk) =s(2-jk)，t∈ [ 0,1]，因此可用s(2-jk)代替s(2-jt+ 2-jk)，因此：

由以上分析可知，当采用 Harr小波基时，如果2j=N，取=s(k/2j)，则连续阶梯函数在Vj中的投影可最佳逼近原函数s。

通过上述证明可发现，对于连续阶梯信号，采用Harr小波基能够很好地逼近。因此，对于光纤陀螺信号实时滤波的问题，采用Harr小波基既可以完美地逼近原函数，又不存在边界问题，是最佳的选择。

3.2 实时滤波算法设计

为实现实时滤波功能，采取滑动窗滤波的方法，在采集到最新时刻陀螺数据后，利用最新时刻及之前时刻的陀螺数据作为待滤波数据。设滑动窗宽度为L，k时刻的光纤陀螺采样值为x(k)，k时刻的实时滤波结果用表示，实时滤波算法的详细实现步骤如下：

① 对窗宽度L（2的幂级数）、分解总层级N进行设置。

② 若k＜L，由于数据量较少，不进行滤波，若kL≥，构造滤波器输入信号序列

③ 使用Harr小波高、低通分解系数对输入信号进行第n级分解，抽二下采样后分别得到细节系数和近似系数

其中：若n=1，则待分解信号为输入信号；若n＞ 1，则待分解信号为n-1层所得近似系数；i的总数取决于每层级待分解信号的长度。

④ 按照一定的阈值处理规则，对多层分解结束后的细节系数进行阈值处理，而近似系数保留。

⑤ 利用Harr小波高、低通重构系数完成对原信号的重构，得到滤波输出序列其中，即为k时刻的实时滤波结果，即完成一次单点的实时滤波。

⑥ 当采样时刻k递增为 +1k时，读入下一个时刻的陀螺信号值，返回步骤②进行下一次的滤波处理。

从实现步骤也可以发现，Harr小波分解的高、低通分解系数的个数都为 2，抽二下采样后可完全消除输入信号外延数据的影响。

4 试验与结果

为对基于 Haar小波基的陀螺信号滤波方法的性能进行评估，分别利用静态陀螺数据和动态陀螺数据进行两组滤波试验。综合考虑滤波效率和性能，滤波窗宽度设置为L= 24=16。窗和窗之间有重叠地向后平移，迭代输出实时滤波结果。

试验一：静态陀螺信号滤波

将光纤陀螺放在静止基座上，令其测量轴位于水平面内并且向东，测得一组静态陀螺数据作为待滤波原信号。分别利用已有Db3小波方法和本文所提基于Harr小波的滤波方法对陀螺实测数据进行滤波。分解总层级设为3级，使用固定阈值法确定阈值，阈值处理方法为软阈值法，滤波结果如图7所示。

从图7(a)可以看到，两种方法都能很好地对陀螺的随机噪声进行抑制，说明小波方法应用于陀螺去噪是可行的。进一步观察图7(b)所示的滤波结果局部放大图，可以看到，基于Haar小波的陀螺信号滤波结果的随机噪声要更小一些。为进一步说明基于Haar小波的滤波方法的优越性，采取3组实测静态数据作为原信号，以标准差作为评判滤波方法性能的标准，对各信号的随机误差进行定量分析，结果如表2所示。

图7 (a) 静态陀螺信号滤波结果Fig.7 (a) The filtered results with static FOG signal

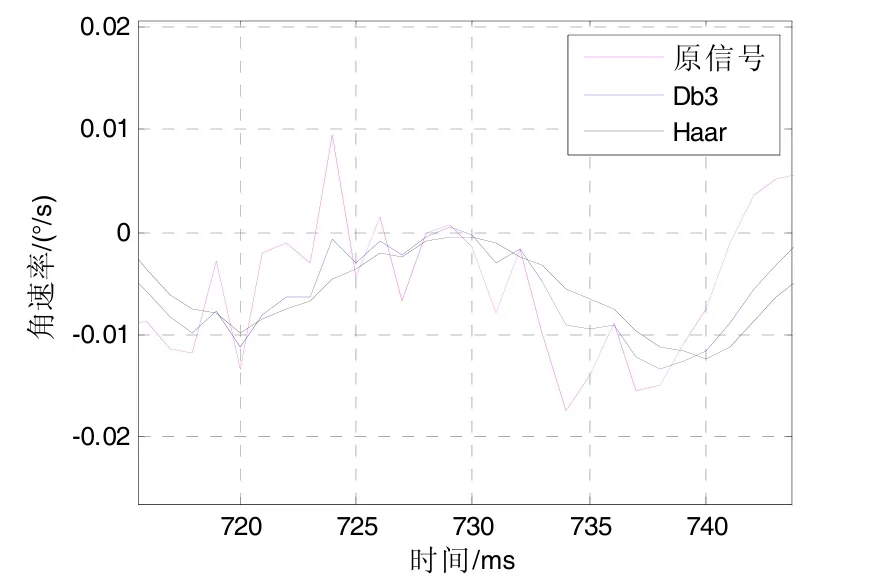
图7 (b) 静态陀螺信号滤波结果局部放大图Fig.7 (b) Partial amplification of filtered results with static FOG signal

表2 基于静态陀螺信号试验的标准差统计结果Tab.2 Statistical results of STD experimented with static signals (°/s)

由于实测数据是静态陀螺数据，假设真值为0的情况下，滤波结果标准差越接近零值越精确，由表2数据可得基于Haar小波的信号滤波方法可更好地抑制随机噪声。

由3.2节算法步骤已知，不同于离线滤波，本文算法是实时进行的。该算法基于TI公司的TMS320F2812芯片实现，代码占用空间为4970byte，满足硬件资源存储需求；运行时长约为106 μs，远小于采样时长1 ms，运算实时性可以保证。为更好地观察陀螺实时滤波效果，对动态陀螺信号展开滤波试验。

试验二：动态陀螺信号滤波

以某惯性稳定平台控制系统（以下简称平台）为对象展开试验，该平台配有三轴光纤陀螺，并安装于电动六自由度摇摆台上。摇摆试验时，平台工作于速度环，其速度响应（即陀螺输出）反映了平台的抗干扰能力，故摇摆试验中常使用速度均方差来衡量平台的稳定精度。

本试验中，在完成对平台的最优PID控制器设计后，以5°/0.5Hz的幅值/频率对平台俯仰向进行摇摆试验，方位向和横滚向无扰动，采用原始陀螺数据（不作任何滤波处理）作反馈，对俯仰向陀螺进行采样，得到平台速度响应曲线如图8所示。受系统响应特性的影响，在每个摇摆周期换向点（即扰动加速度最大点）处，平台会出现较大的稳定误差，从而使陀螺输出如图8所示的频率约为1 Hz的尖峰信号。

图8 基于滤波前陀螺信号闭环的速度响应Fig.8 Speed response of platform without using filtered signal in closed-loop calculation

对如图8所示的原始陀螺数据进行基于本文算法的半实物仿真滤波试验，为保证通用性，参数设置同静态陀螺滤波试验，滤波结果如图9所示，滤波前后信号频谱图如图10所示。

图9 动态陀螺信号滤波结果Fig.9 The filtered result with dynamic FOG signal

从图9所示滤波结果可以得出，对于动态陀螺信号，本文方法仍可以有效地降低随机噪声，进一步说明本文方法用于实时陀螺滤波的有效性。图10所示滤波前后信号频率成分类似，说明滤波的实施未损失原信号的带宽。滤波后信号与原信号包络对比，存在约5 ms时间的滞后，对于速度闭环系统（带宽约几十赫兹），此滞后时间完全可以接受。

为定量地评估实时滤波方法对实际平台综合性能的影响，直接使用在线实时滤波后信号闭环，重新进行最优PID控制器设计并开展同条件摇摆试验，新的速度响应信号如图11所示。

对分别使用滤波算法前后陀螺信号闭环时，所对应的速度响应均方差进行统计，结果如表3所示。试验结果说明，在对陀螺原始信号进行滤波，并以其作为速度反馈后，由于反馈信号质量的提升，光纤陀螺噪声对系统带宽的制约降低，从而可在最优PID控制器的基础上进一步上调比例系数，最终测试平台的稳定精度提高约14%。

表3 滤波前后的平台速度响应均方差Tab.3 Mean square errors of speed response before and after using filtered signal

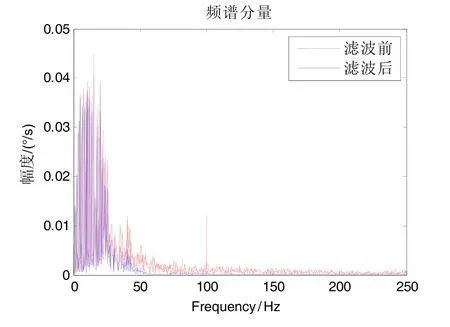
图10 滤波前后信号频谱图Fig.10 Spectrum diagram of signals before and after being filtered

图11 基于滤波后信号闭环的速度响应Fig.11 Speed response of platform corresponding using filtered signal in closed-loop calculation

5 结 论

本文首先从Mallat算法步骤的角度出发，对数据越界现象进行描述。然后通过仿真说明，基于Daubechies类小波方法存在严重的边界问题，对于实时陀螺滤波并不适用。进而通过理论分析，详细证明了Harr小波在本文背景下的适用性相关问题。最后提出一种基于Haar小波的实时陀螺信号滤波方法，并进行了两组基于静态和动态数据的滤波试验，最终验证本文所提方法对于提升实际惯性稳定平台控制系统的积极作用。