利用小波变换分析电能质量扰动问题中的电压骤升影响

熊隽迪，崔世海

（1.重庆电力高等专科学校，重庆 400053；2.长安福特汽车有限公司，重庆 401120）

1 模拟电压骤升数学模型

本文实验所用的电压骤升波形如图1所示。其中，电压有效值、频率以及采样频率与电压骤降波形相同，电压在t=0.3 s发生骤升，在t=0.3 s时恢复，持续时间0.4 s[1]。数学模型为：

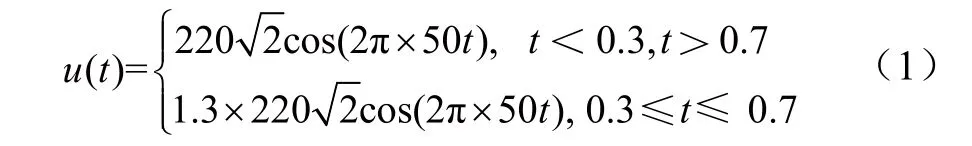
2 用四种小波基分解和重构信号

分别利用Haar、Db4、Coif4和Sym4四种小波基处理信号，分解尺度为3。分解后的小波系数在四种小波基函数下的近似系数重构比较图如图2所示，细节系数重构比较图如图3所示[2]。

在此次仿真中，Haar小波基分解和重构电压骤升信号的效果不理想，其余三种小波基函数能够有效检测电压骤升的突变点[3]。

3 检验四种小波基的重构误差

四种小波基的重构误差数据如表1所示。

由表1中可知，本次仿真所用波形，当小波分解尺度为3，采样频率为6.4 kHz时，Haar小波基的重构误差最小，其次为Sym4小波，Coif4小波的重构误差最大[4]。

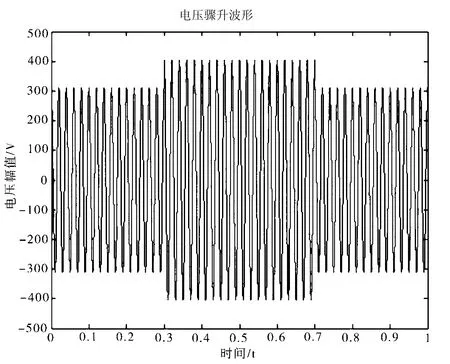
图1 电压骤升信号模型

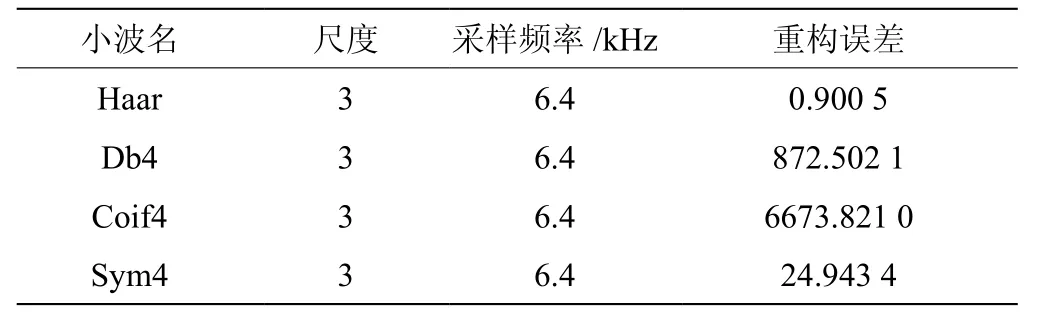
表1 四种小波基函数分解重构误差

4 检验四种小波基对故障点的定位情况

四种小波基对故障点的定位情况如表2所示。

由表2可知，模极大值与模平均值之比除Haar小波基外，其余三种小波基函数均远大于100，证明在该点发生了较为明显的突变。同时，再一次说明Haar小波基奇异点的检测效果不佳，抗干扰能力与奇异点的识别能力在一定程度上低于其余三种小波基函数[5-6]。

电压骤升起始点、恢复点的理论值与测量值数据如表3所示。

由表3可知，Db4、Coif4和Sym4三种小波基在电压骤升信号在尺度为3的分解和重构中，电压骤升起止点的测量误差控制在10-3数量级内，奇异点检测效果良好。

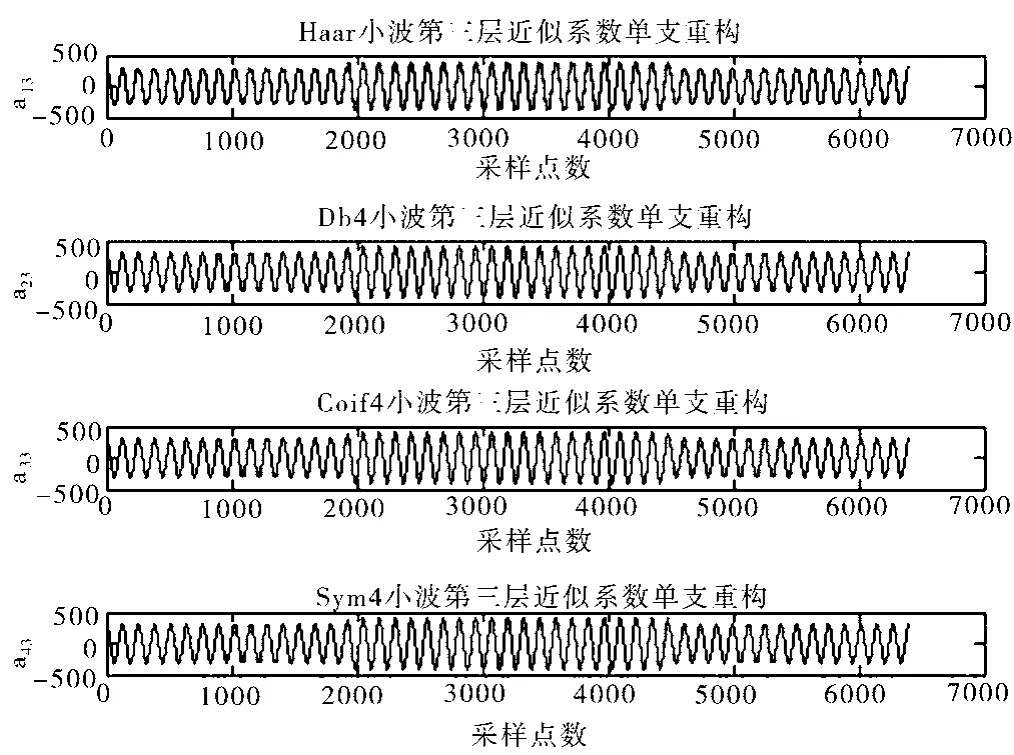
图2 四种小波基函数近似系数重构波形

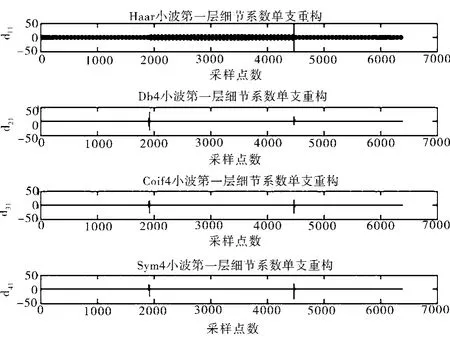
图3 四种小波基函数细节系数重构波形

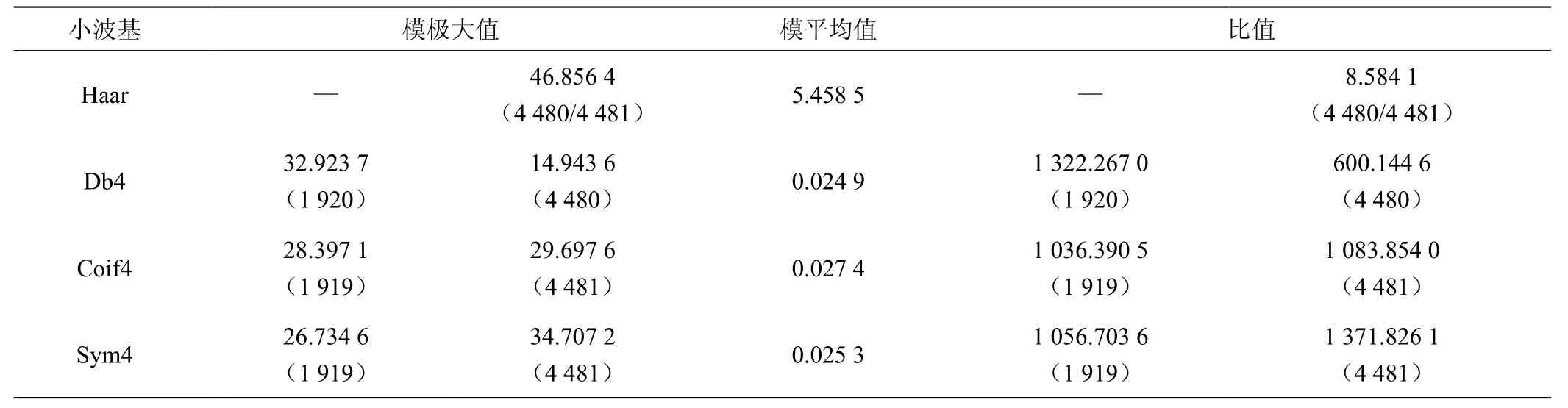
表2 细节系数的模极大值与模平均值

表3 电压骤升起始点、恢复点的理论值与测量值比较

5 结 论

本文利用四种小波基仿真分析暂态电能质量的电压骤升扰动信号发现，Haar小波作为最经典、最基础小波函数，虽然重构误差最小，但是时域不连续、正则性很差。它不能定位故障的起始点，故障恢复点的模极大值与模平均值比值较小，不能有效检测奇异点。而Db4、Coif4和Sym4三种小波基可以定位故障的起始点与恢复点，具有较为明显的模极大值。但是，在定位精度上，Coif4和Sym4小波基定位故障起始点和恢复点时具有10-3数量级的误差，Db4小波基则完全没有误差，重构误差也较小。因此，综合考虑奇异点定位精度与重构误差等因素，选择Db4小波基函数检测电能质量信号的奇异性最合理。