基于共形阵列天线的DOA估计

梅锦洲

（广东盛路通信科技股份有限公司，广东 佛山 528100）

0 引 言

共形天线是一种和物体的外形结构保持一致的天线或天线阵。共形天线可方便地装备于载体表面而不影响载体的空气动力学性能，此外，共形天线可采用柱面阵列和锥面阵列等形式，实现了广角扫描，并在扫描中保持天线的波束形状和增益。共形天线可使互耦维持在一定范围，并具有隐形特性[1]。共形天线在卫星通信、指挥和控制系统、导弹遥测、武器信管及多普勒雷达等学科占据重要位置，因此建立了数学模型，并利用Matlab软件对传统算法和子控件类算法进行共形阵列天线DOA的仿真分析[2]。

1 共形阵列天线接收信号模型

为简化共形阵列天线的分析，假设入射信号的特性为平稳且各态历经，用时间平均代替统计平均；噪声为白噪声，方差为σ2n；忽略共形天线各阵元之间的互耦和极化因素；入射的信号数小于阵列天线阵元数，且阵列接收到的所有信号互不相关、波达方向互不相同；假设信号为窄带信号，阵元接收的信号之间无包络变化[3]。圆锥共形阵列天线的模型如图1所示。

其中，每层圆阵中逆时针方向的阵元编号为N（N=0，1，2，…，n-1）；圆阵自上至下的层数为M（M=0，1，2，…，m-1）；相邻圆阵之间的间距为d；锥顶角为α。各阵元用直角坐标系可表示为：

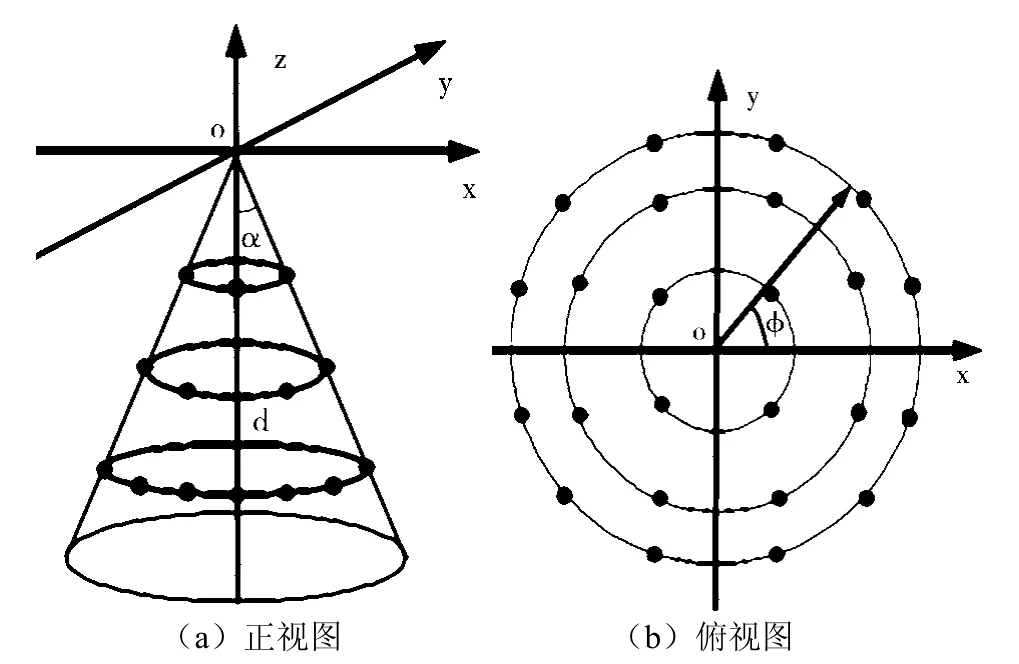
图1 圆锥共形阵列天线示意图

其中，RMN=Mdtanα。那么t时刻L个远场信号Si入射到锥面共形阵列天线上时，阵列天线接收信号可表示为：

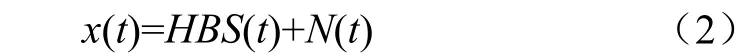
其中，x(t)为接收信号矢量，H为阵列方向图矩阵，B为导向矢量矩阵，S(t)为来波信号矢量，N(t)为加性噪声矢量矩阵。

式（2）是基于建立圆锥共形阵列天线的接收信号的模型，且不考虑极化和互耦的条件下，利用数学知识推导多个互不相干的远场信号以不同的方向入射到共形天线各阵元的接收信号。圆锥共形阵列天线在俯仰面上通常使用和圆柱共形阵列天线相同的波束扫描方法，尖锐的圆锥共形阵列天线可为实体提供良好的空气动力学性能、低雷达散射截面及宽角覆盖。

2 MUSIC算法

多重信号分类（MUSIC）算法是1979年R.O.Schmidt等人提出。该算法的提出促进了特征结构分类算法的发展[4]。

假设阵元方向图为全向，则窄带信号的DOA估计的数学模型为：

其中，x(t)为接收信号矢量，B(θ)为导向矢量矩阵，S(t)为来波信号矢量，N(t)为加性噪声矢量矩阵。

接收信号的协方差矩阵为：

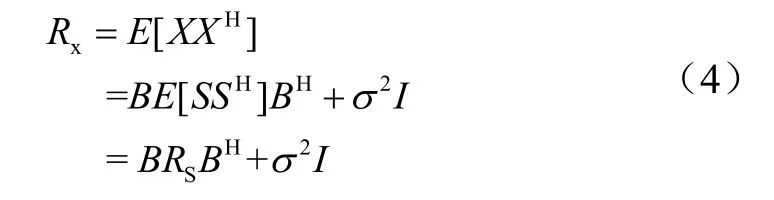
其中，B为导向矢量矩阵，RS为入射信号的协方差矩阵，BH为导向矢量的共轭转置矩阵，σ2为噪声方差，I为单位矩阵。

由于信号与噪声是独立的，所以接收信号协方差矩阵可分解为信号与噪声两个部分，对Rx进行分解可得到：

其中，Us是信号子空间，Un是噪声子空间。

理想的条件下，噪声子空间和信号子空间是相互正交的，所以有：

其中，bH(θ)为导向矢量的共轭转置

MUSIC算法是基于上述性质提出的，但是接收数据协方差矩阵是用有限采样数据的最大似然估计值：

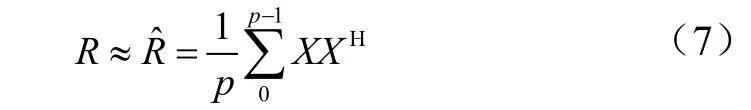
Music算法是对空间谱函数PMUSIC进行谱峰值搜索，得到最大值P对应的θ值即为来波信号的DOA。具体算法步骤为：由阵列接收的样本数据X(t)得到数据协方差矩阵；对进行特征分解；确定噪声子空间和信号子空间；根据信号的参数范围进行搜索MUSIC空间谱，找出谱峰；得到谱峰值时所对应的角度θ，即为信号的波达方向。

3 MATLAB软件仿真

模型1：均匀圆阵模型中，阵元M=20，空间中信号L1和L2分别从俯仰角θ1为30°、θ2为70°，方位角φ1为60°、φ2为150°入射，信号频率f为5 GHz，噪声方差σ2=0.1，均匀圆阵的半径r为1.5λ。

在Matlab软件中采用MUSIC算法对模型1进行DOA仿真，仿真结果如图2所示。

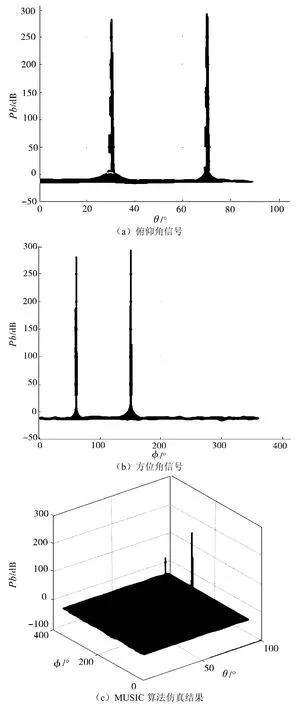
图2 模型1仿真结果

由图2可知，MUSIC算法在模型1中完全能识别出波达方向。

模型2：锥面共形阵列天线模型中，阵元M=25，空间中信号L1、L2及L3分别从方位角φ1为60°、φ2为65°、φ3为70°，俯仰角 θ1为35°、θ2为40°、θ3为45°入射，信号频率f为5 GHz，噪声方差σ2=0.1，信噪比均为10 dB。圆锥的锥顶角α为20°，两相邻均匀圆阵之间的间距d为0.1 m。对模型2进行仿真分析，仿真结果如图3所示。

图3 模型2仿真结果

由图3可知，信噪较低的环境下，MUSIC算法仍能估算出波达方向。

4 结 论

本文基于已建立的锥面阵列天线模型详细推导应用于DOA估计的MUSIC算法，利用MATLAB软件基于MUSIC算法对均匀圆阵模型和锥面共形阵列天线模型进行DOA估计仿真。仿真结果验证了MUSIC算法在DOA估计中的可行性。