基于橡胶等效动态模量的惯导减振装置设计方法

杨盛林，芈小龙，王晓丹，李德春,3，刘 伟，刘 旭

（1.天津航海仪器研究所，天津 300131；2.海军装备部，北京 100841；3.中船重工集团有限公司航海保障技术实验室，天津 300131 ）

为提升惯性导航系统在诸如舰船作战时的大冲击载荷、陆用车辆高速行进中的长时间颠振以及飞机、导弹飞行过程中的高频振动等各种恶劣环境中的适应性，一方面通过模态分析方法优化惯导系统结构[1]；另一重要方面是为其加装减振装置，以提高惯导系统适应范围的广度和深度，改善惯性元件的工作条件，保证系统稳定的输出精度。

橡胶减振装置具有体积小、重量轻、设计灵活度高以及低成本等诸多优势，现已被广泛采用。橡胶减振器作为橡胶减振装置的重要减振元件其数学模型和力学性能研究还不太充分和深入。近年来，许多专家学者针对减振器用橡胶材料的力学特性进行分析研究。宓宝江等人[2]提出了一套超弹性材料模型的本构方程和材料系数拟合方法，但是该数学模型只能进行静力学分析，无法模拟减振装置在振动条件下的整体响应。马咏梅、黄巍等人[3]给出了基于试验方法将非扭转橡胶减振器等效为一维弹簧模型的刚度与弹性模量之间的换算关系。高军强[4]和Tu Yongqiang[5]等人分别定量分析了橡胶减振器对捷联系统和双轴平台系统输出的影响。Abrahammsson、Arsla M E和Abdur R等人[6-8]利用有限元方法对含有橡胶减振器的减振装置进行了仿真分析。而Gong Dao[9]和Zeynali Keyvan[10]等人曾通过试验方法来拟合减振器的动态公式。综上，对于橡胶减振装置的主要减振元件--橡胶减振器的研究主要有两类：试验和仿真。传统的研究方法就是基于试验测试的结果对减振装置进行改进，这样会使结构设计成本增加，周期延长。随着计算机软硬件的迅猛发展，基于仿真分析的研究方法被广泛采用，然而，大部分的仿真分析模型是将橡胶减振器简化为弹簧-阻尼单元，该模型虽然简单直接，但是无法将减振器几何形状、预紧力以及与结构件的配合关系反映到模型中，势必会对模型的精度产生影响。

为此，本文针对橡胶减振装置的设计和应用需求，通过试验拟合和理论推导相结合的方式构建了包含几何形状、预紧力和结构件配合关系的橡胶动态弹性模量数值计算经验公式，形成了一套适合于分析橡胶减振装置性能的数学仿真模型，总结出一套切实可行的橡胶减振装置设计方法，实现了仿真数字化分析指导橡胶减振装置设计的目标。

1 橡胶减振装置理论建模

1.1 橡胶减振装置数学模型构建

橡胶属于超弹性近似不可压缩体，基于应变能密度函数的本构理论是描述这种材料特性的有效理论之一，如式(1)所示：

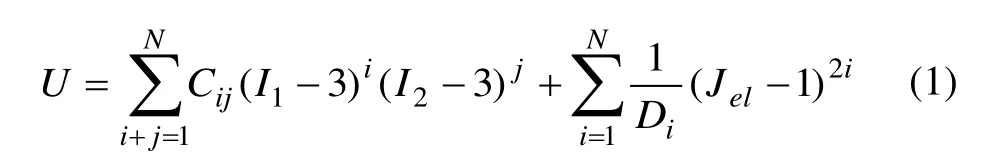
式中：U是应变能密度函数；N是项数；Cij和Di分别为橡胶材料的剪切特性和可压缩性；Jel是弹性体积比；I1和I2分别是第一、第二偏应变不变量。

从式(1)的复杂度可以看出，由于该公式的建立需要大量的试验数据支撑，而现实工程应用过程中很难对采购的橡胶胶块进行多项力学测试，该公式并不适合于工程分析，需要构建更加简化并且高效的数学模型。

研究证明，拉伸状态下，橡胶材料先软化再硬化；压缩状态时，材料急剧硬化，且呈线性，显示出与拉伸不同的力学状态。橡胶材料制成减振器时为了提高其承载能力和线性度，通常情况下为受压状态。而橡胶材料在预压力的作用下变硬，其等效动态弹性模量会发生变化。对于橡胶材料在受压状态下的小变形弹性行为，可通过三维数字仿真分析平台上带有预应力的模态分析模型来构建橡胶减振装置的数学模型，即首先进行非线性的静态橡胶受压分析，然后对含有内应力计算结果的三维模型进行动力学分析。

在该数学模型中，结构形式、减振器布置方式、负载重量、减振器几何尺寸等对减振装置动力学响应有影响的因素都可以直接反映在三维实体模型之中。然而，变化的等效动态弹性模量却是未知数，需结合橡胶材料硬度、减振器与结构件的配合程度、减振器的预紧位移等因素构建关系式间接反映到减振装置的数学模型中。因此，构建橡胶等效动态弹性模量关系式是决定减振装置数学模型准确与否的关键因素。

1.2 橡胶减振装置测试试验

对于橡胶等效动态弹性模量关系式的构建首先需要进行大量试验，本文中选取了硬度、配合方式、胶块约束方式、负载重量完全不同的两套结构进行试验测试，并用来与理论推导公式进行数据拟合。

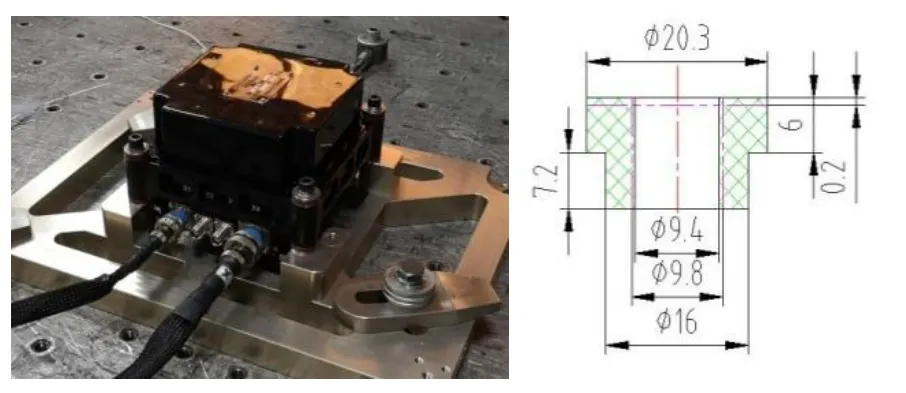
图1 橡胶减振装置A和橡胶减振器几何尺寸Fig.1 Rubber damping device A and its physical dimension

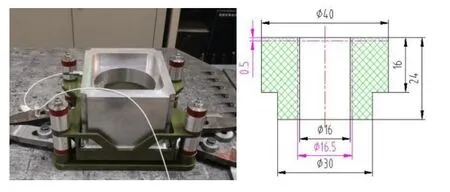
图2 橡胶减振装置B和橡胶减振器几何尺寸Fig.2 Rubber damping device B and its physical dimension

由于橡胶减振器形式多种多样，本文选择自主设计程度最高且制作周期最短的T型橡胶减振器作为研究对象。第一种橡胶减振装置结构如图1（左）所示，在被减振设备（重约4 kg）四个角处设计上下安装的四对橡胶减振器，其几何尺寸见图1（右）所示。第二种橡胶减振装置结构如图2（左）所示，被减振设备重约10 kg，四个角点上下安装四对橡胶减振器，几何尺寸见图2（右）。装置A分别选取了30度、40度和55度三种不同邵氏硬度（HA）的T型橡胶减振器进行测试，而装置B分别选取了30度、40度和60度。以上几种邵氏硬度的T型橡胶减振器基本可以覆盖工程化应用。

表1列出了橡胶减振装置A和B的试验测试数据，根据表中所列数据可以看出装置A的共振频率随着橡胶的邵氏硬度增加而快速升高；然而装置B的共振频率虽然与橡胶邵氏硬度也成正比例关系，但是变化幅度与装置A相差甚大。这说明橡胶邵氏硬度不是影响减振装置动力学特性的唯一因素，橡胶减振器的几何尺寸、与结构件的配合关系、预紧力以及负载重量等因素都有密切关系。

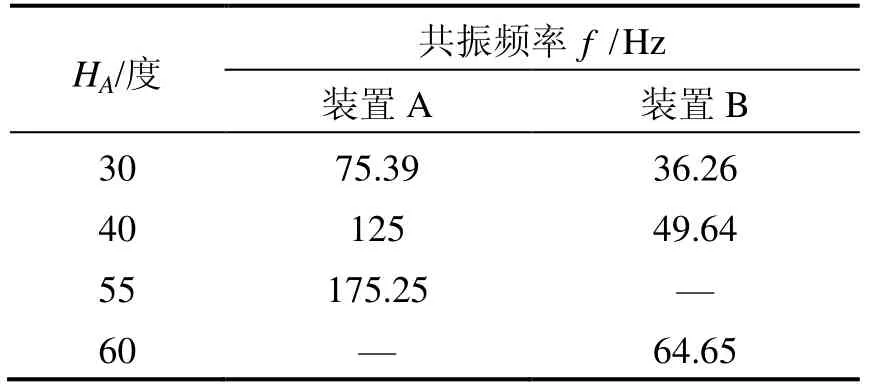
表1 胶减振装置A和B的试验测试结果Tab.1 Test results of rubber damping device A & B

1.3 橡胶减振器等效弹性模量经验公式构建

在已有的静态弹性模量关系式中引入动力影响系数并体现上节中提到的影响减振装置动力学响应因素。

文献[1]给出了橡胶初始（静态）弹性模量与邵氏硬度之间的经验公式：

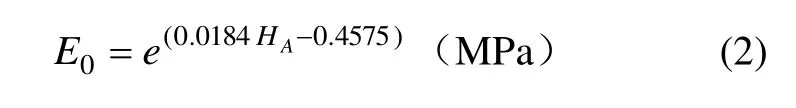
式中：HA为橡胶的邵氏硬度；E0为橡胶初始弹性模量。

根据表1的试验测试结果分析可知，橡胶减振器的邵氏硬度、橡胶减振器的几何尺寸以及与结构件的配合关系等因素对减振装置的动力学响应都起着显著影响。参考应变能密度的表达公式以及减振器等效刚度参数的计算方法，给出动力影响系数KG（与几何形状 Geometry相关）和KP（与橡胶受力程度 Pressure相关）的表达式。

动力影响系数KG与橡胶胶块的几何形状有直接关系，可用式(3)表示：

式中：A1表示橡胶胶块总的表面积大小；A2为橡胶胶块允许自由变形的表面积大小。

该项参数意味着，当橡胶受来自一个方向的压力P，则由于材料本身的不可压缩属性势必会使橡胶朝另外两个方向释放变形。橡胶受限运动的表面比例越大，则会使橡胶变形释放不完全，积聚在内部的变形能越大，则橡胶刚度越大。

图3中A、B、C、D四幅图显示了T型橡胶减振器的主要约束形式。其中黑色轮廓线表示未受力的自由状态，而粉红色轮廓线表示受力之后的状态。P表示来自结构件给橡胶施加的预应力。用橡胶总面积除以自由面积则表示橡胶形变能转化为动力能量的程度。其中装置A的橡胶减振器属于图3中的A型；装置B的橡胶减振器属于图3中的B型。

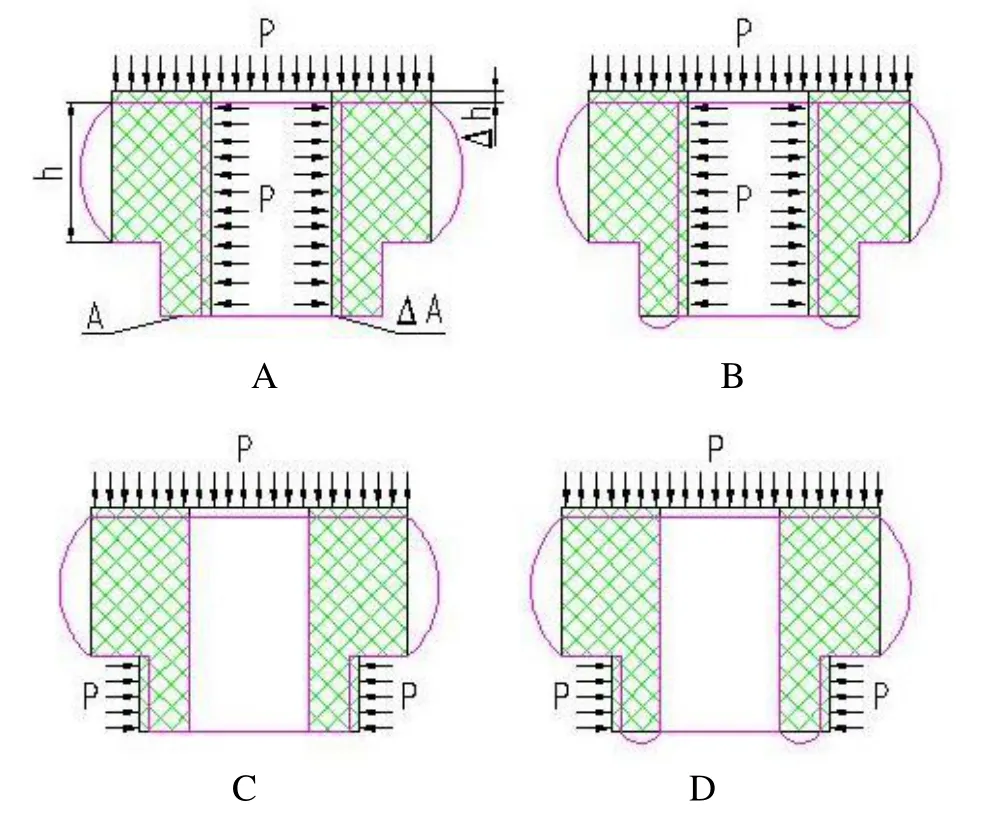
图3 T型橡胶减振器受力的四种基本形式Fig.3 Four basic types of applied forces on T-type rubber damper

动力影响系数KP是与橡胶胶块的预紧量以及橡胶胶块与减振支架的装配过盈量来定义的：

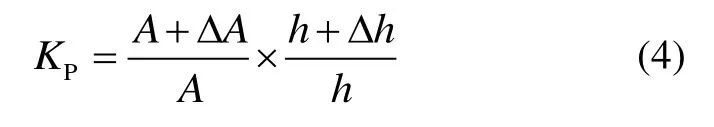
式中：Δh是橡胶所受预紧量；h为受预紧量作用后的总高度；A是受过盈影响的总的截面积；ΔA为受过盈量影响的截面积改变量（如图3中A型所示）。

通过初步推导，可以将上述两项动力学影响系数KG和KP与初始弹性模量E0相乘，既可以得到等效动力学弹性模量E t1，如式(5)所示：

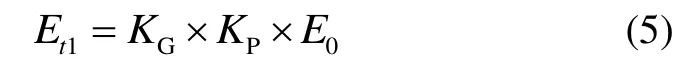
表2列出了A和B两套减振装置中对应的不同邵氏硬度的橡胶减振器初始静态弹性模量E0和等效动力学弹性模量Et1。

然而，将Et1的对应数值代入到减振装置A和B的数学模型中进行仿真计算，发现所得的谐振频率f（见表2中所列数据）在低邵氏硬度范围内远远大于实际测试结果（见表1中所列数据），而高邵氏硬度范围内又比较接近或者略低于实际测试结果，说明式(5)给出的等效动力学弹性模量没有完全反映出两套减振装置不同的动力学响应趋势，需要进一步修正。在此，引入动力影响系数KM（与橡胶本身材料Material属性相关），如式(6)所示：

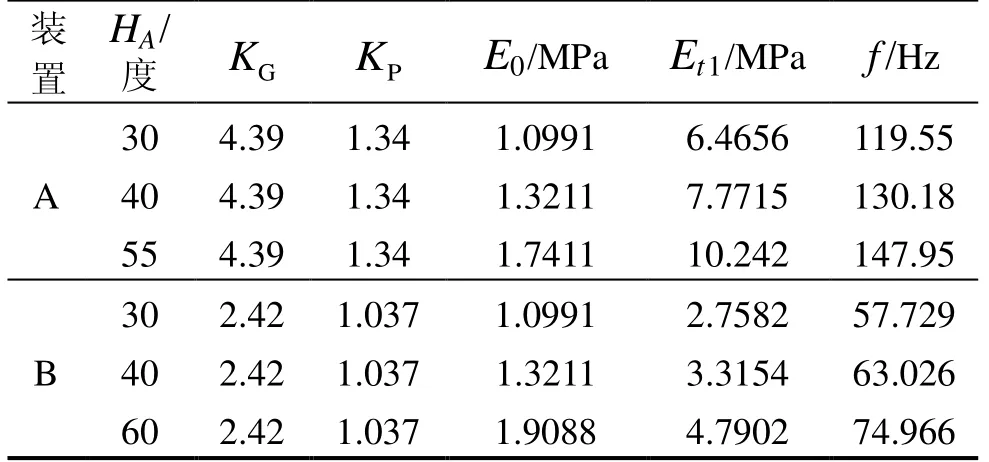
表2 两种减振装置的等效动力学弹性模量Tab.2 Equivalent dynamic elastic modulus of two rubber damping devices

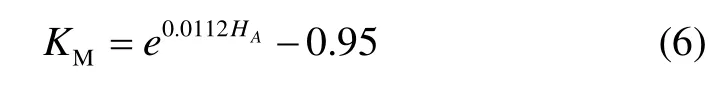
得到等效动力学弹性模量Et2：

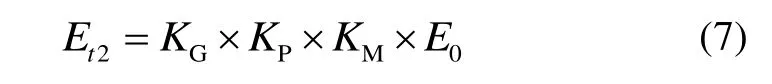
将通过式(2)得到的静态弹性模量、式(2)～(5)得到的等效动力学弹性模量Et1以及式(2)～(4)(6)(7)得到的修正过的动力学弹性模量Et2计算得到的结果均列在表3中进行对比。修正过的Et2公式可以有效改善静态弹性模量偏柔以及解决Et1无法覆盖两套减振装置不同的动力学响应趋势的问题。

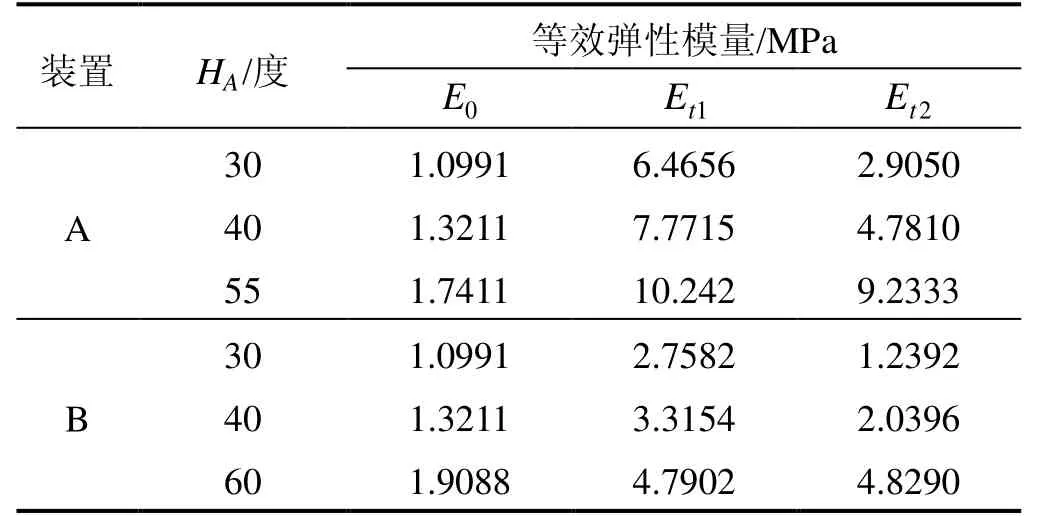
表3 随邵氏硬度改变的等效动力学弹性模量Tab.3 Equivalent dynamic elastic Modulus with hardness changing

图4显示了初始静态弹性模量E0和等效动力学弹性模量Et1以及修正的动力学弹性模量Et2与橡胶邵氏硬度之间的变化关系（动力影响系数KG和KP取值来自装置A）。

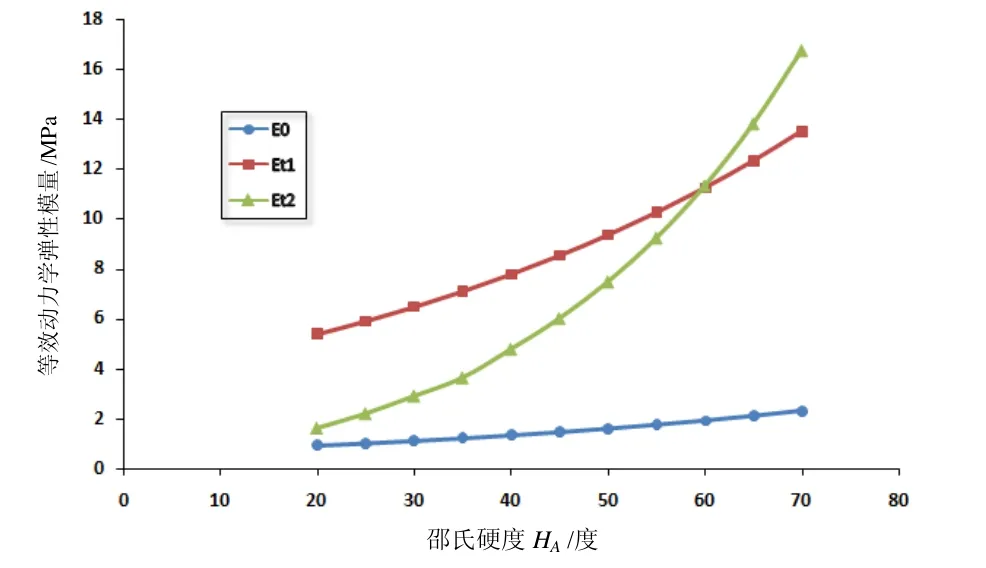
图4 邵氏硬度与等效弹性模量关系示意图Fig.4 Relationship between hardness and elastic modulus

从图4中可以看出等效动力学弹性模量Et1通过引入动力影响系数KG和KP可有效将橡胶所受约束和与结构件的配合关系等影响因素引入到计算模型之中，将等效动力学弹性模量数值提高，即橡胶所受的约束和预紧会使橡胶变硬。而在此基础上引入动力影响系数KM所得到的修正后的等效动力学弹性模量Et2可以真实反映出邵氏硬度对动力学响应变化趋势的影响。因此，式(2)～(4)(6)(7)构成了T型橡胶减振器的等效动力学弹性模量的经验公式。利用Et2得到仿真数值解与试验测试值的对比结果，见表4。

其中，符合度P定义为：

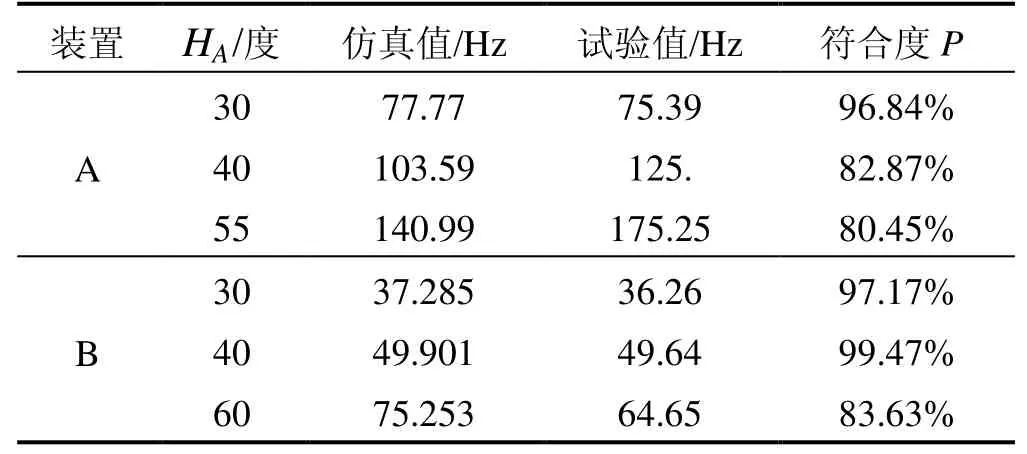
表4 试验测试结果与数值计算结果的对比Tab.4 Test results and simulation results

表4中仿真值与试验值之间的符合精度均大于80%，准确程度高。本文提出的橡胶减振装置的数学模型将高度非线性材料利用经验公式等价为线性分析方法，将原来无从下手的减振器动力学仿真分析变为可能，同时还提高了求解精度和效率。

2 惯性导航设备的橡胶减振装置设计方法

利用本文提出的橡胶材料的等效动力学弹性模量经验公式，结合减振装置数学模型的构建方法，橡胶减振装置设计采用下述方法进行：

① 根据被减振惯性设备的重量、重心位置以及所对应的力学环境计算目标共振频率f0；

② 惯性设备减振器的分布尽量空间对称。根据输入条件，确定减振器设计大致方案以及橡胶胶块的大概布置形式；

③ 预先给定胶块几何参数和装配关系，进而利用式(3)(4)确定KG和KP。

④ 将常用的邵氏硬度参数带入到式(2)(6)中，确定E0和KM。

⑤ 利用式(7)得出Et2，与泊松比一起带入到减振装置数学模型中进行仿真计算。将计算得到的f与设计目标共振频率f0相对比。如果不相同可以从材料邵氏硬度、几何形式和装配关系以及橡胶布置形式等四个方面进行微调，最终得出最佳方案，并将与目标要求最接近的模型完善设计细节，最终出图投产。

需要特别指出的是，在橡胶减振器装配完成以后，由于新采购的橡胶块存在着不稳定的力学性质，需要对橡胶减振器进行多次重复的加-卸载试验循环以后才能保证橡胶减振器在与之加-卸载相同的力学环境中E0的稳定性。因此，在橡胶减振装置交付使用之前须对其分别进行不低于 5次的加-卸载试验以及实际试验条件的力学环境试验以保证橡胶减振装置处于稳定的状态。同时应该注意的是，应该对每块T型橡胶减振器进行标记，保证每块橡胶减振器在每次加-卸载过程中安装位置的一致性。

3 橡胶减振装置振动试验验证

为了验证本文所提出的橡胶减振装置数学模型以及设计方法的正确性，现有一重量约为4 kg，目标共振频率为50 Hz的减振装置的设计输入，根据上述设计方法，设计了一套三点上下支撑的橡胶减振装置C，见图5所示，其橡胶减振器约束形式为图3中的D型。利用经验公式计算得到的等效弹性模量以及仿真和试验值的对比见表5所示。

通过表5中列出的试验测试值和仿真数值解对比的符合精度远远大于80%，数值模型能够满足工程化分析需要，可以指导橡胶减振装置的设计。

从表5中的数据可以看出，装置C配置30度的T型橡胶减振器可以满足设计输入的需求。将装配了30度橡胶减振器的装置C进行实际系统测试，在实际测试环境中，系统精度满足使用要求。

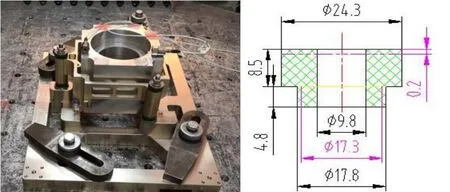
图5 减振装置C和减振器几何尺寸Fig.5 Rubber shock absorber C and physical dimension of rubber damper

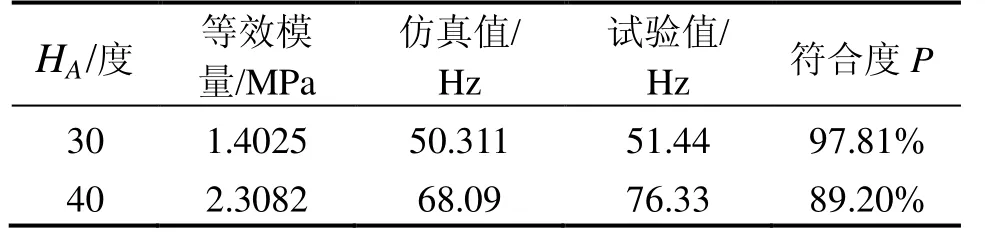
表5 装置C的材料参数和数值/试验结果Tab.5 Elastic modulus of rubber damper in device C and test/simulation results

图6 减振装置C的系统测试试验Fig.6 The system test of device C

因此，利用本文所提出的橡胶减振装置数学模型可准确估计减振装置的动力学响应，基于本文提出的设计方法可有效缩短设备研制周期。

4 结 论

为了使惯导系统适应小尺寸、大动态、强冲击等恶劣力学环境，提高系统适应性，对惯导系统加装的减振器必须有清晰的认知并且尽量缩短设计周期以达到快速响应市场需求的能力。本文基于等效动力学弹性模量公式构建了可靠的工程化橡胶减振装置数学模型；基于此模型，总结出切实可行的橡胶减振装置的设计方法。对利用该方法指导设计的数学模型和实物进行了仿真和试验测试。从将近90%的数学模型符合精度以及惯导系统在各项力学环境测试中的良好表现可以得出以下结论：

① 经过数值与试验对比验证，本文所提出的橡胶邵氏硬度与等效动力学弹性模量的经验公式是具有可靠性和高效性的橡胶材料参数等价公式；

② 基于橡胶材料的等效动力学弹性模量所构建的含有非线性应力的预应力模态分析数学模型能给出准确的橡胶减振装置的动力学响应分析结果；

③ 基于本文提出的数学模型，所提出的减振装置的设计方法具有很强的可操作性，可大幅度缩短橡胶减振装置的研制周期、降低研制成本，提升惯性系统的耐振、抗冲环境适应性。