基于二次解析的UWB室内定位高度方向优化方法

徐晓苏，刘兴华，杨 博，王 帅

（1.微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2.东南大学 仪器科学与工程学院，南京 210096）

UWB（Ultra-wideband）技术近年来广泛应用于室内定位，它具有频带宽 、空间和时间分辨率高、穿透性强、保密性好、定位精度较其他定位方法高、基本不干扰其他信号的传播等优点。UWB定位是一种基于无线电的定位技术。UWB的定位原理可分为基于达到时间的方法（Time of arrival,TOA）、基于到达时间差的方法（Time difference of arrival,TDOA）、基于到达角的方法（Angle of arrival,AOA）和基于接收信号强度的方法（Received signal strength indication,RSSI）等[1]。基于飞行时间的方法（Time of flight,TOF）最能发挥UWB的优点，因此当前的方法大多是基于TOA或TDOA。

当前UWB定位使用较多的解析法定位技术方案是基于TOA的最小二乘法（Least Square,LS）、Taylor级数展开法，基于TDOA的Chan算法，三角形质心法等[2-3]。在二维室内空间环境下这些算法能够由UWB测距信息快速解算得到目标的定位初值，是其他方法的基础。然而，在三维室内环境中，上述方法在高度方向上提供的解算值具有很大的不确定性，往往难以得到较为准确的高度坐标值，甚至得到的解算值是错误的，这限制了上述方法的应用。此外，一些组合方法，如UWB与IMU（惯性测量单元，Inertial Measurement Unit）组合方法[4]或UWB与视觉SLAM（即时定位与地图构建，Simultaneous Localization and Mapping）组合方法[5]等，需要应用传统解析法得到的初值，这要求一种能够在具有高度限制环境下给出正确初值的解析定位方法。文献[6]对三维定位问题作了研究，针对Chan算法提出了基于Tikhonov正则化的鲁棒岭估计方法，但文献没有分析导致方程组性态差的原因，且文献方法在选择正则化参数时需要结合L-曲线法多次迭代确定，增加了应用难度。由于岭估计引入了偏差，文献[6]方法在基站不存在布置限制问题时，将导致解算误差比传统解析法大。

本文通过对UWB室内定位常用解析法的研究，分析了传统解析法在高度方向定位精度较差的原因，并针对传统解析法在三维室内定位环境下由于基站布置具有限制而无法给出正确解算值的不足，提出一种二次解析方法（Reanalysis Method,RM）以改善高度方向的定位效果。该方法先根据传统解析法求解出水平方向定位值的解析解，然后在二次解析过程中利用修正偏差的Tikhonov正则化方法（Tikhonov Regularization,TR），求解得到较为精确的高度方向的定位值。

1 针对传统解析法的分析

1.1 传统定位方程组的机理分析

定位解算时采用解析法求解UWB定位目标值，实质上是利用定位方程组直接求解目标点坐标。本文首先介绍传统定位方程组的分析方法，然后利用该方法分析基于传统解析法UWB定位精度不高的原因。传统定位方程组一般为一组线性方程组，通过将UWB测距信息代入方程组，求解出目标点的位置值。假设定位方程组有如下形式：

其中，A为系数矩阵，b为常值向量，θ为待求解的位置值。由于UWB测距值带有误差，求解上述方程组将不可避免地产生求解误差。根据数值分析中方程组误差分析的知识，在系数矩阵A与常值向量b分别有误差δA和δb的情况下带来的解θ的误差范围为

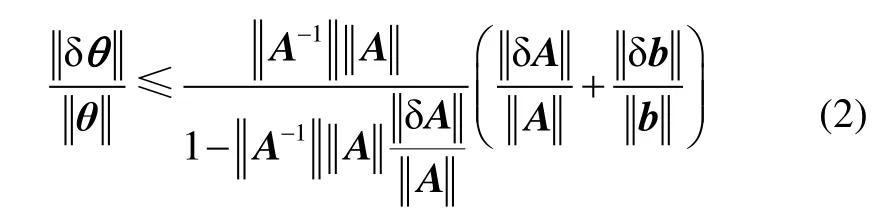
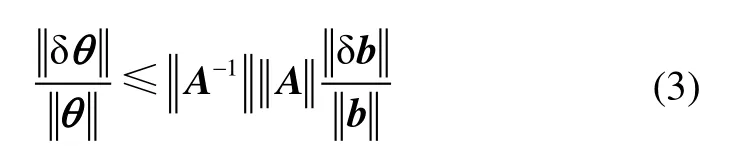
对于2条件数有：

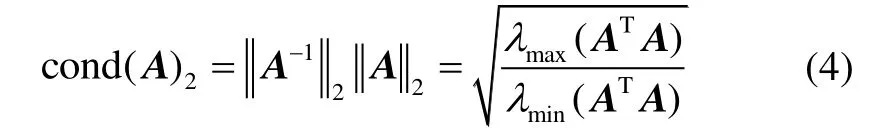
其中，λmax(·)和λmin(·)分别表示矩阵的最大和最小特征值。若系数矩阵对称正定，则有：

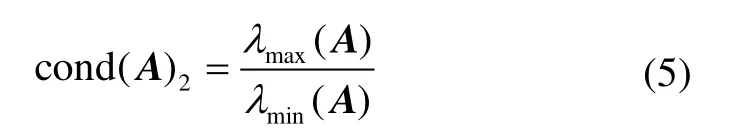
1.2 解析法常用的定位方法与定位方程组

将常用的UWB定位算法对应的定位方程组表述在三维定位情况下，可得如式(6)～(9)形式。其中基于TOA的n(n≥4)基站最小二乘法定位方程组为

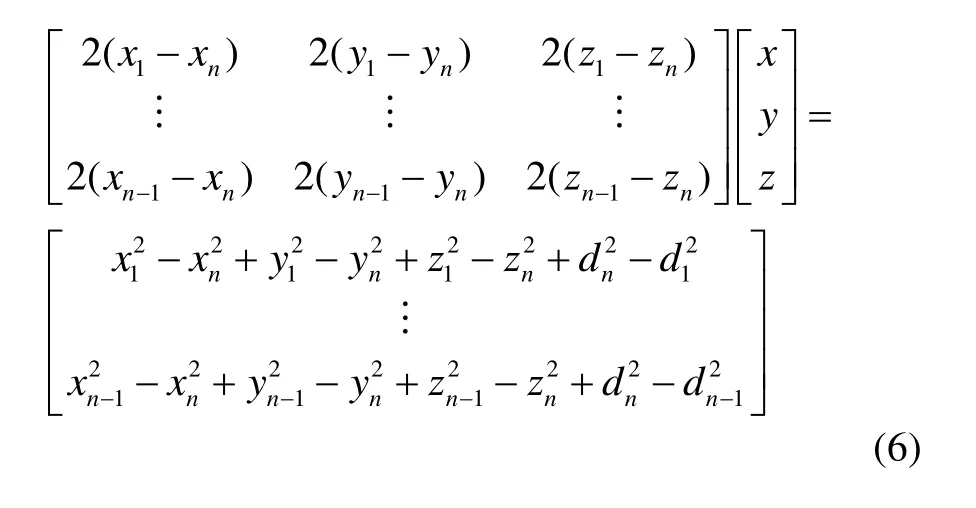
基于TOA的泰勒展开定位方程组为[7]：

基于TDOA的Chan算法第一次极大似然估计使用的定位方程组为

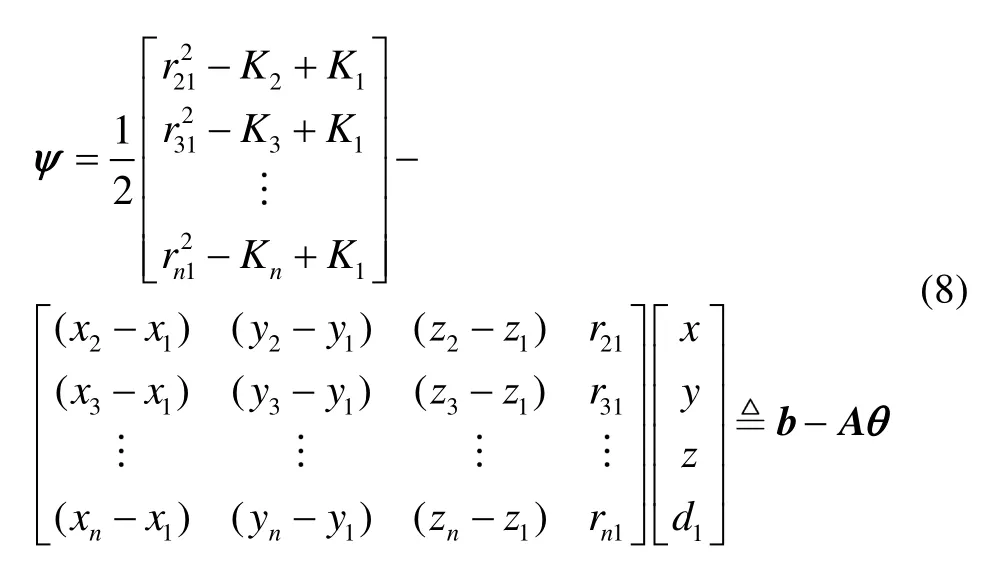
式中，ψ为误差向量，ri1(i= 1,,n)为定位目标点到第i(i= 2,,n)个基站的距离与到第 1个基站的距离的差，参数

Chan算法采用两次极大似然估计减小测距差误差对目标定位的影响。

三角形全质心算法是针对二维定位情况提出的，在二维定位情况下具有较好的鲁棒性。该算法形式上满足式(1)，因此可以采取相同的方法分析，故本文也对其进行分析。三角形全质心算法的定位方程组为

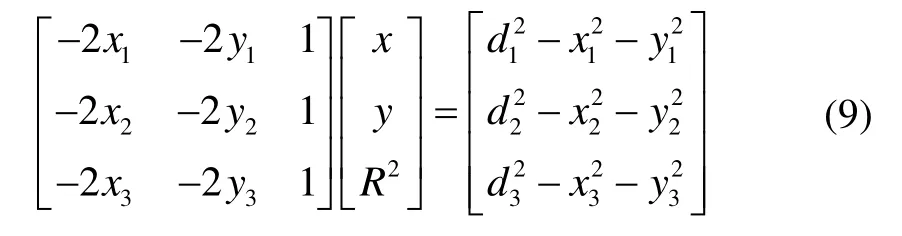
式中，R2=x2+y2。

由此可见，前面给出的几组定位方程，均可写成式(1)的形式，可以按照1.1节的方法讨论基站测距误差对解的影响。通常情况下，认为UWB基站的位置是比较精确的，而基站的测距误差或测距差误差是影响解的主要因素。所以可以认为，解的误差主要是由误差δb引入的。以下的讨论也是基于此观点。

1.3 室内UWB定位高度方向精度不佳的原因分析

在UWB定位的实际环境中，通常在布置基站的时候，对平面方向（x、y方向）的限制比较小，可以布置在比较合理的范围，而对高度方向（z方向）的限制比较大。这是因为室内楼层的高度有限，一般的楼层大多在3～5 m的范围内。以下讨论说明，这是导致UWB定位高度方向上精度不佳的主要原因。

对于任意目标节点有如下关系式：

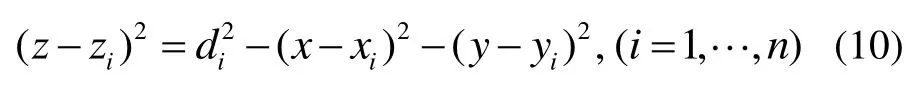
在式(10)中，分别利用前n-1式减去第n式，当0时可得：

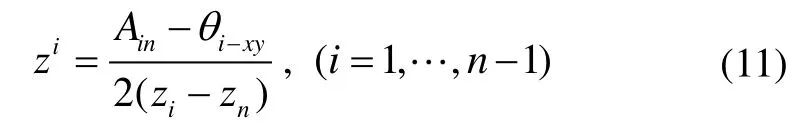
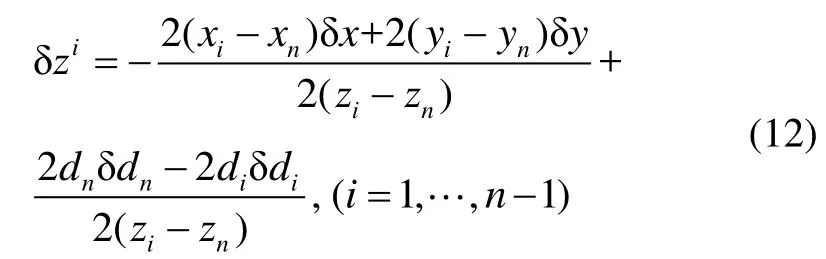
为方便得出其中的规律，假设各基站的测距误差均相等，且到定位目标点的距离大致相当，可以得到：

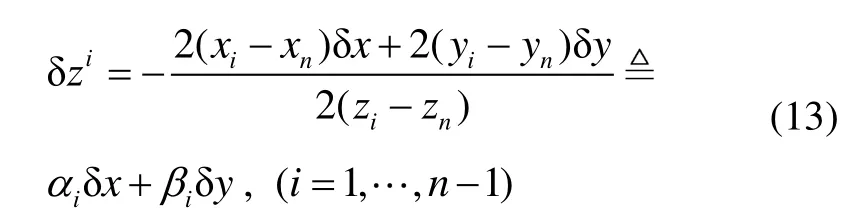
式(13)描述的距离比例因子还可看作是各算法定位方程组的系数矩阵中的元素的数量级之间的关系，最明显的是式(6)和式(8)。距离比例因子越大，说明系数矩阵中的元素数量级差别越大，矩阵越有可能是病态的，因测量误差带来的解的不确定性越大。

2 解析法在高度方向定位精度不佳的解决方法

前面指出，解析法在高度方向上定位精度不佳的主要原因是基站在方向的距离差相比于基站在方向（高度方向）上的距离差较大。因此对于采用解析法提供初值的定位技术方案中，可以采取两种思路解决上述问题：其一是尽量将基站布置在成球对称位置或近似球对称位置，这样将使得各方向上的误差最小且一致[8]；其二是采取别的办法减小解算误差。通常 UWB室内定位无法将各基站布置成球对称位置，因此本文将根据第二种思路求取解决办法。

2.1 影响定位精度主要的分量分析

以下首先针对鲁棒性较好适用范围广的最小二乘法进行讨论，然后提出一种提高解析法解算时高度方向的位置准确度的方法。首先分别对UWB室内定位的两种情况做讨论。二维定位情况（不包含高度方向）下，根据式(1)和式(3)最小二乘法的定位方程组系数矩阵的2条件数为

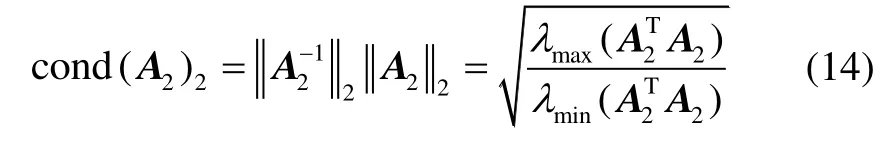
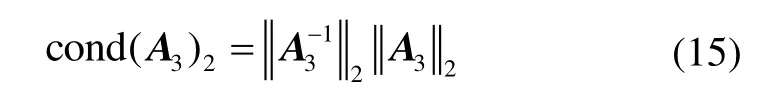
较大，其中A3是处理三维定位问题时对应的系数矩阵。为简单说明问题考虑以下系数矩阵：

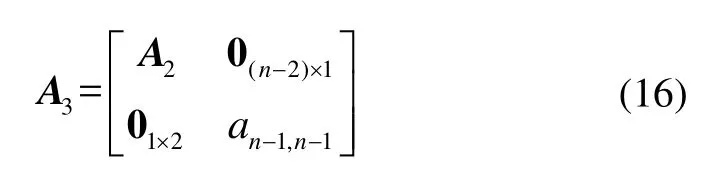
其中：an-1,n-1为考虑三维定位问题时，因某个基站高度值变化使得系数矩阵维数增加而引入的参数；式(16)中的参数an-1,n-1= 2(zn-1-zn)；A2为对角元不为0，其余元素均为 0的矩阵。只有四个基站时，矩阵A2=diag{2(x2-xn),2(y3-yn)}为对角阵。由于水平方向基站布置限制少，因此可认为 (x2-xn) ≈ (y3-yn)，于是

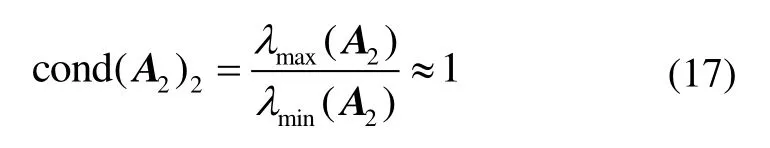
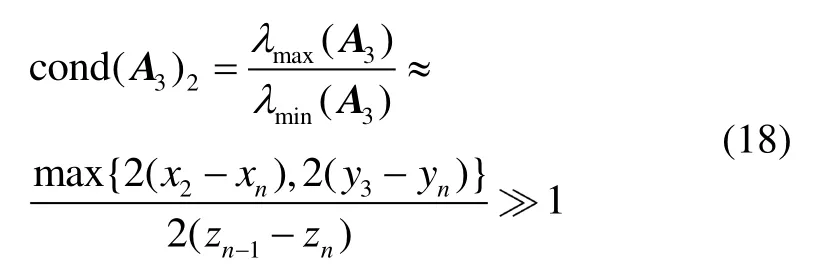
其中，max{・}表示集合中元素的最大值。

式(17)和式(18)表明，方程组的病态是由于高度方向的引入引起的。上述也可说明高度方向的解算误差δz是引起解向量不确定性增大的主要因素，即δz在中起主要作用。因此可以考虑保留第一次解析解算初值中的前两个变量(x,y)的解算值，而对高度方向的变量解算值再进行二次解析解算。

2.2 修正偏差的Tikhonov正则化方法

根据Tikhonov正则化理论[9-10]，其估计准则为

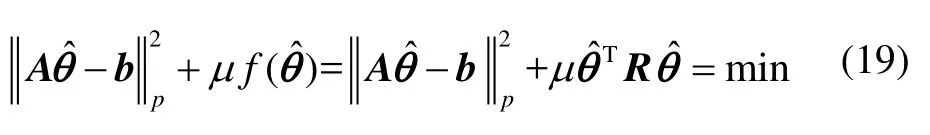
其中，μ为正则化参数，为θ的估计值，R为正则化矩阵，f(θ)为稳定泛函，表示矩阵p-范数。当R=I时，该估计方法被称为岭估计。求解式(1)描述的不适定问题的岭估计公式为

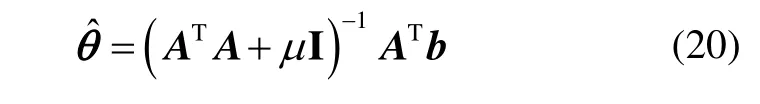
但式(20)的正则化参数μ难以确定，且所得的估计结果是有偏的。以下根据Tikhonov正则化的思想，提出一种修正偏差的Tikhonov正则化方法，并介绍确定修正偏差Tikhonov正则化矩阵的简单方法。

根据矩阵的幂级数展开有：

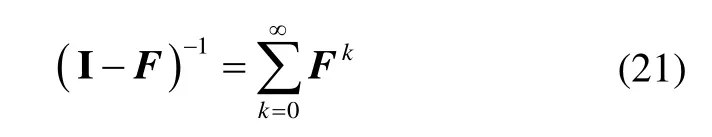
其中，F为方阵。若矩阵F的谱半径ρ(F)＜1（或，则 Neumann级数收敛于则有：

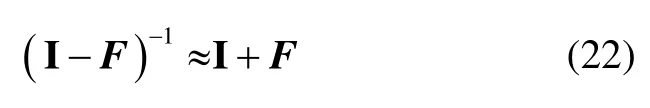
考虑对称正定矩阵ATA（A列满秩）的Cholesky分解

则有：

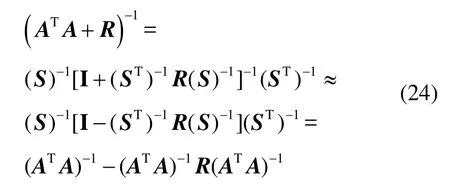
上述推导过程中，要求谱半径ρ((ST)-1R(S)-1)＜1，且要求 ((ST)-1R(S)-1)2≅0。由式(24)可以得到：

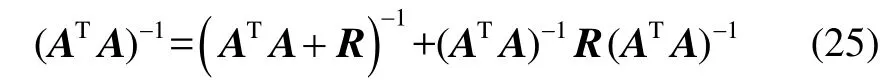
根据式(19)描述的准则，可得到估计值的计算式：

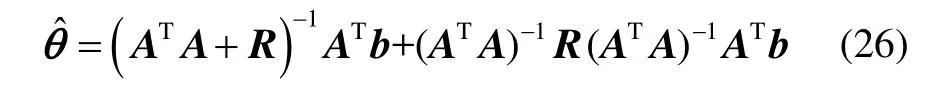
式(26)说明，表征等式右边第二项的是与R、ATb相关的项。实际上ATA的逆矩阵包含较大的特征值，直接用式(26)计算会带有较大计算误差。将式(26)中的(ATA)-1进行修正，得到：

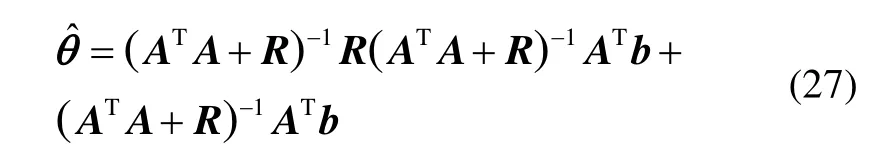
式(27)的实质是通过对 (ATA)-1的进一步近似，来修正引入正则化矩阵R带来的偏差。当式(27)的正则化矩阵R满足式(19)时，不论高度方向是否存在限制，理论上均可取得最优值。式(27)中R的取值一般要满足前面矩阵谱半径的要求，在实际中可取R=diag(0,0,γ)，其中的参数γ与ATA的最小特征值或前文所说的最大距离比例因子相近较好，前者能够保证估计量整体能够近似无偏且能够较大程度地降低估计误差，后者能够尽量降低z方向的最大估计误差。同时，基于最小二乘法的无偏性，可利用最小二乘法的估计均值，来近似确定Tikhonov正则化方法的整体偏差，以取得Tikhonov正则化的大范围近似无偏解，有：

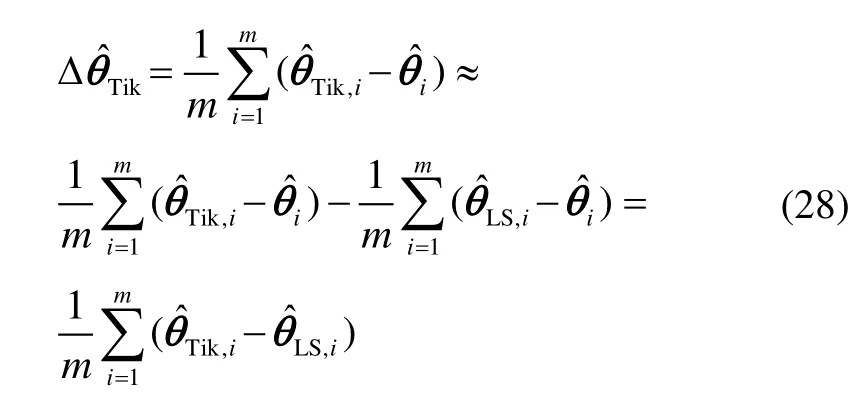
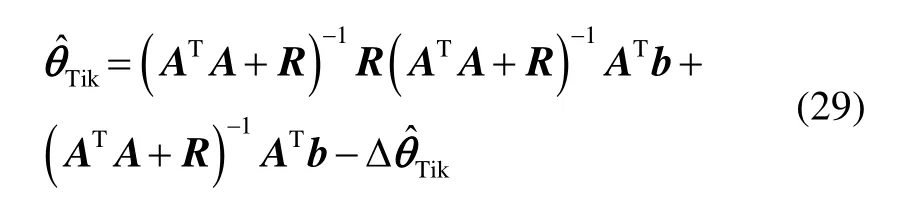
根据求解的精度要求，可以重复式(28)和式(29)进一步优化估计值，即

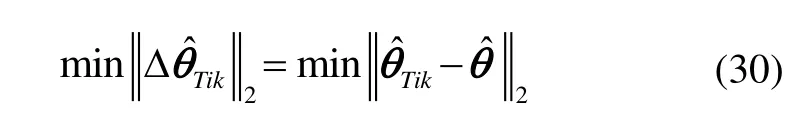
上述求解过程首先需要进行一次 LS估计，其次需要根据式(27)再次对目标点进行估计，然后将两次估计按式(28)相减得到偏差，最后修正估计值的偏差。

3 仿真与实验验证

为了验证本文观点以及验证文中提出的二次解析法，本文通过 MATLAB仿真与样机实验将本文提出的方法与传统的Chan算法和最小二乘法进行对比。由于Taylor展开已难以收敛，故未与其进行对比。

3.1 仿真验证

仿真条件设置如下：UWB基站的距离测距误差为 0.1 m，设置了 5个 UWB基站，其位置分别为(0,0,0)、(6,0,0)、(0,5,0)、(3.5,3,0)、(3,2.5,0.5)。

然后对1350个独立空间点各进行一次仿真定位。1）距离比例因子与矩阵条件数Z方向误差的影响

图1是最小二乘法的仿真实验结果。图1的实验中高度不为0的基站其高度依次为2.5 m、1.25 m、0.5 m。在此实验中，令某个基站的高度产生变化以改变距离比例因子和系数矩阵条件数。从图1可以看出，距离比例因子越大，系数矩阵的条件数也越大，高度方向（z方向）的误差也越大。同时可以看出，高度方向的误差是影响室内三维定位精度的关键。值得一提的是，相同基站布局下不同算法的系数矩阵条件数不同，且定位误差对测距误差的敏感程度也不同。由于Taylor展开法与三角形质心法的系数矩阵与最小二乘法的类似，也仅与基站的坐标相关，所以这两种算法的结果可以参考最小二乘法。虽然 Chan算法第一次极大似然估计的系数矩阵不仅与基站的位置相关还与移动节点的位置相关，但其定位误差与系数矩阵条件数的关系依旧满足最小二乘法的结论，限于篇幅没有将结果放在文中。

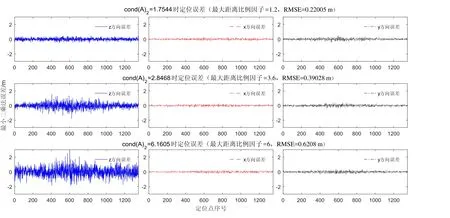
图1 最小二乘法系数矩阵与定位误差的关系Fig.1 Relation between the least square coefficient matrix and the positioning error

2）修正偏差的Tikhonov正则化法与最小二乘法、Chan算法对比

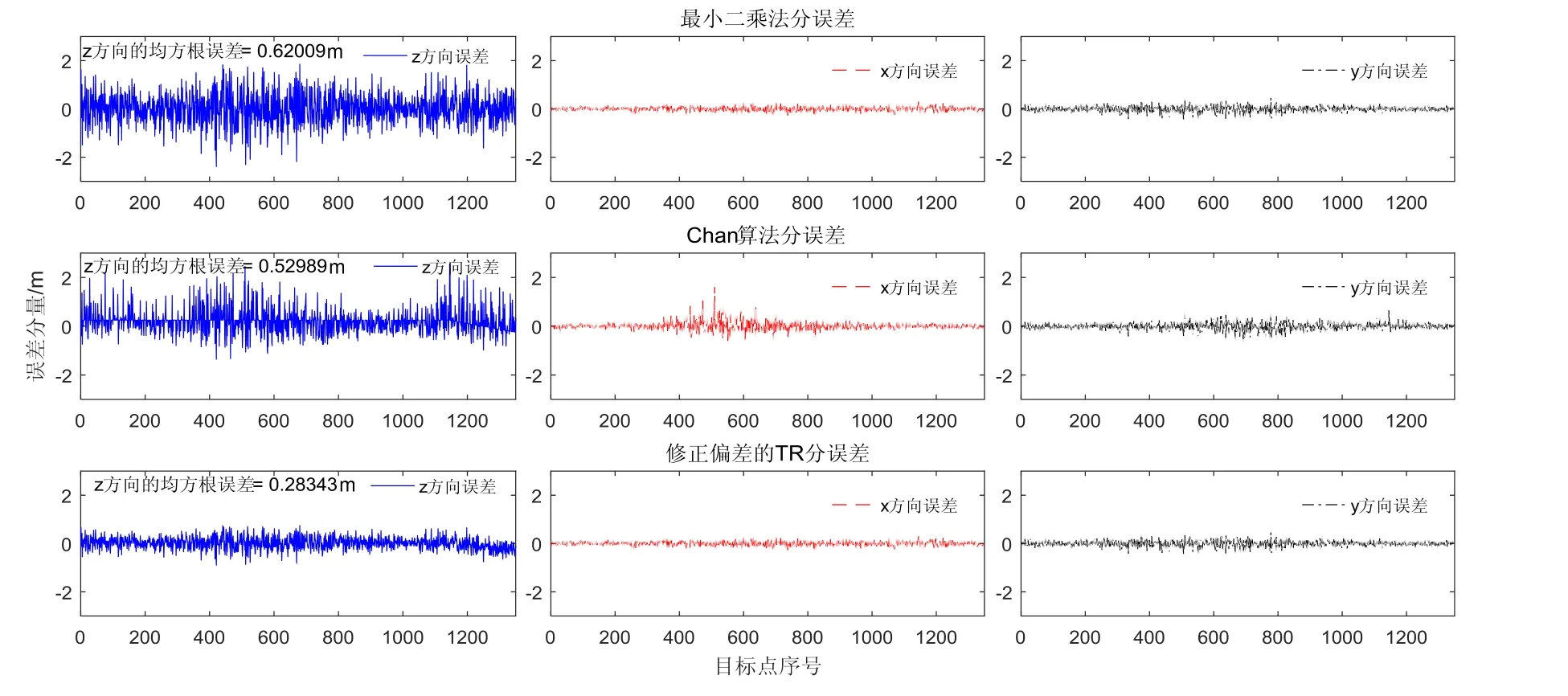
图2 几种算法误差分量对比Fig.2 Comparison on error components of the three algorithms

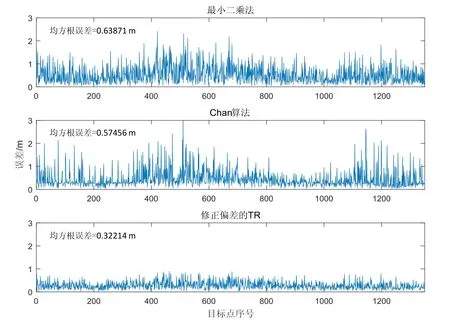
图3 定位误差效果对比Fig.3 Comparison on positioning error effects

从图2、图3可以看出，影响Chan算法与最小二乘法三维定位的主要因素是高度方向的误差，与图1实验所得结论一致。虽然基于二次解析的修正偏差的Tikhonov正则化法（TR）的主要误差也是高度方向的误差，但是相比于前面两种算法，该TR方法能够有效利用目标点的一次定位信息，降低高度方向的误差。TR方法总误差比最小二乘法减小49.6%，比Chan算法减小43.9%，均超过40%。从图2和图3可以看出Chan算法部分定位误差比最小二乘法定位误差要大，这是因为 Chan算法易受基站分布与测距误差影响，且在室内三维定位的环境下，高度方向的误差急剧增大，使Chan算法其他两个方向的估计误差增大。

上述仿真结果说明，具有严重高度限制的 UWB室内三维定位的定位精度主要取决于高度方向的定位精度。在室内环境中应尽量增大基站的高度差，尽量减小距离比例因子以减弱方程组的病态。

3.2 实际样机实验

1）样机实验条件与实验环境

实验采用Decawave公司的DWM1000作为定位模块，实验前先对定位模块的测距值进行标定，定位实验时对目标点（移动节点）进行独立测量，然后利用测量数据对目标点进行定位解算。实验场所为环境复杂的实验室，实验采用激光测距仪测量移动节点的真实起始位置。本实验环境中使用的激光测距仪其测距原理基于光的粒子性质，其测量精度优于±5 mm。实验中设置5个UWB基站，其位置（单位为m）分别为(0,0,0)、(5.035,0.640,0)、(1.942,1.881,0)、(0.010,3.951,0)、(1.745,1.989,0.5)，然后对搭载移动节点的无人车在多个位置点进行定位，其中无人车做匀速运动。

图4为搭载移动节点的无人车实物照片。

本实验采用研创物联公司的UWB Mini3sPlus开发板对目标点进行测距。研创物联公司的 UWB Mini3sPlus开发板以Decawave公司的DWM1000作为定位模块。定位模块与激光测距仪的性能指标如表1所示。

实验环境以及基站布置的位置示意图如图5所示，其中基站BS3的高度与其他四个基站的高度不同，而其他四个基站的高度均相同。

实验时定位点所在的轨迹如图6所示。

表1 定位模块与激光测距仪的性能指标Tab.1 Performance indexes of positioning module and laser rangefinder

图4 搭载移动节点的无人车Fig.4 Unmanned vehicle with mobile node

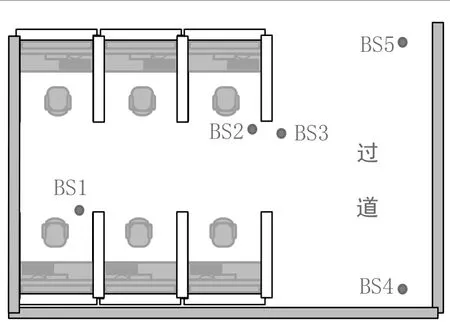
图5 实验环境以及基站布置示意图Fig.5 Schematic of experimental environment and base station layout

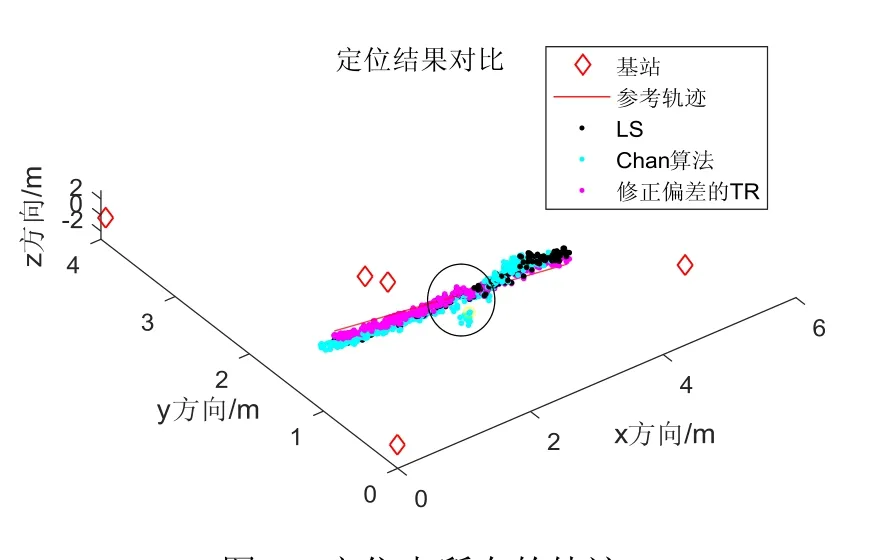
图6 定位点所在的轨迹Fig.6 Trajectory with positioning points

2）样机实验分析

样机实验的结果如图7和图8所示。从图7的实验结果可以看出，在基站高度方向布置受到限制的情况下，影响定位误差的主要因素是高度方向的定位误差，与文中分析和仿真实验结果一致。同时可以发现，Chan算法在前段时间出现误差近似平滑的现象。这主要是因为 Chan算法解算时其解算过程值出现了平方值为负数的情况而被强制转为零。从图8中还可发现，用 Chan算法解算时，中间段部分位置的解算误差突然变大。导致这一现象的原因是目标点处在这些位置时（图6中黑色圆圈的位置），目标点到部分基站的距离近似相等，使得用 Chan算法解算时相应的逆矩阵接近奇异。修正偏差的Tikhonov正则化法则不会出现Chan算法的情况。

综合图7和图8可以得出，本文提出的修正偏差的Tikhonov正则化法能够降低定位方程组的病态，能够同时降低最大误差，高度方向的定位误差，从而有效降低三维定位的误差。本文提出的修正偏差的Tikhonov正则化法相比于最小二乘法能在高度方向上提高53.0%，总体定位效果提高52.1%，相比于Chan算法能在高度方向上提高 41.1%，总体定位效果提高41.6%，均超过 40%。三种算法的定位均方根误差（Root-mean-square error,RMSE）如表2所示。

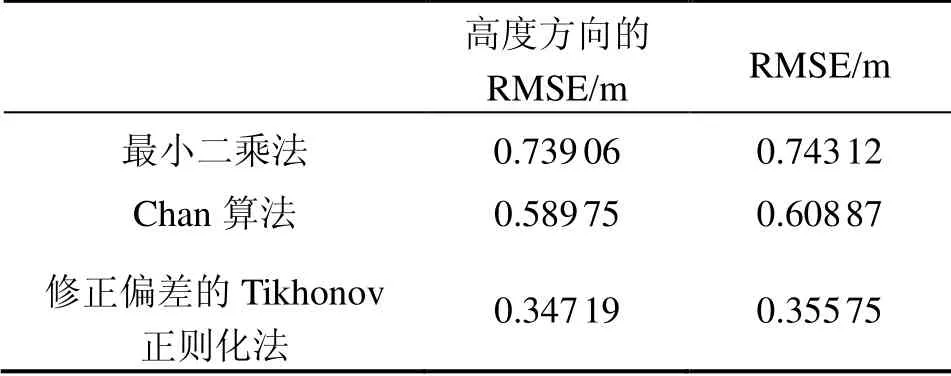
表2 三种算法均方根误差Tab.2 Root-mean-square errors of the three algorithms

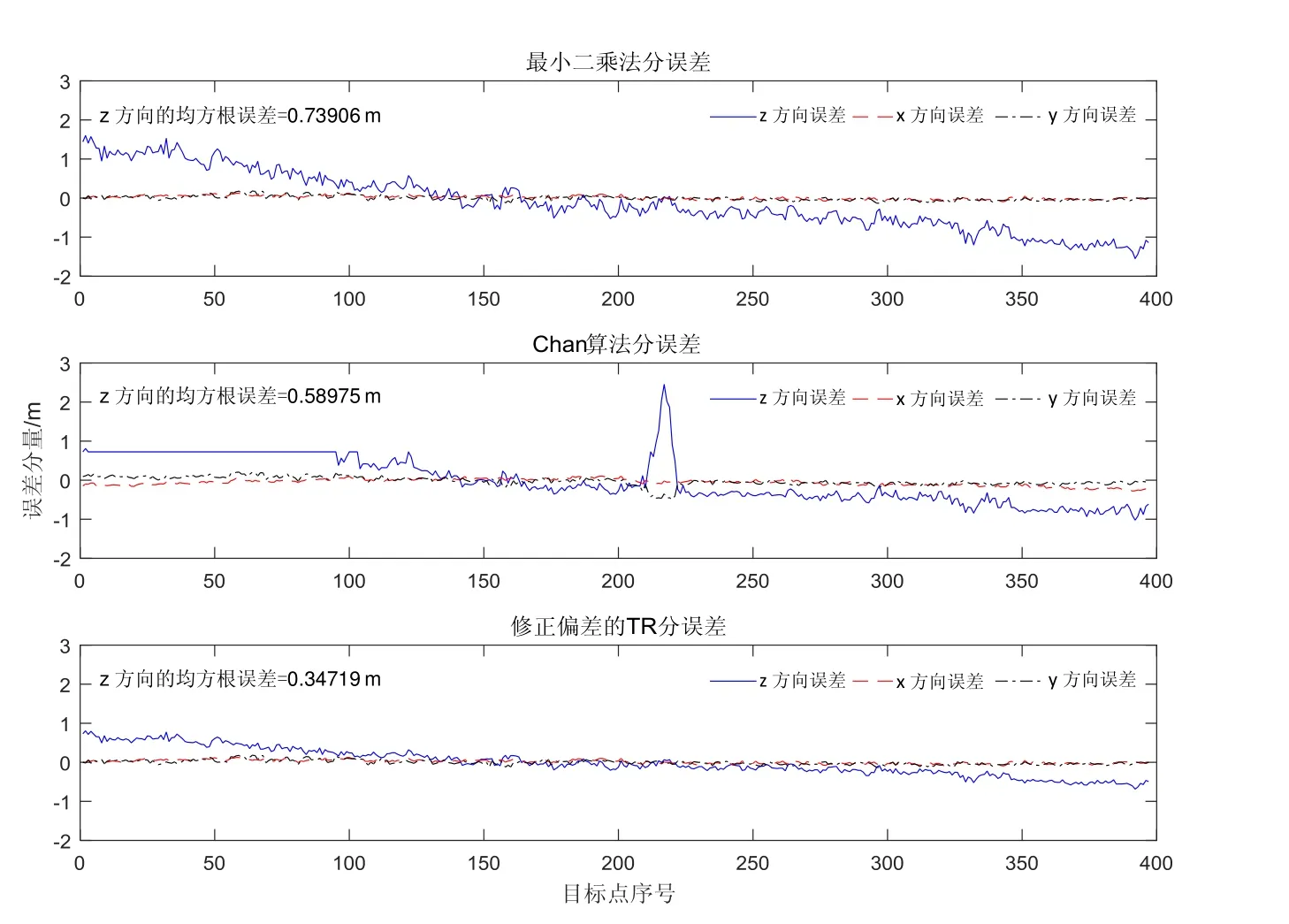
图7 误差分量对比Fig.7 Comparison on error components

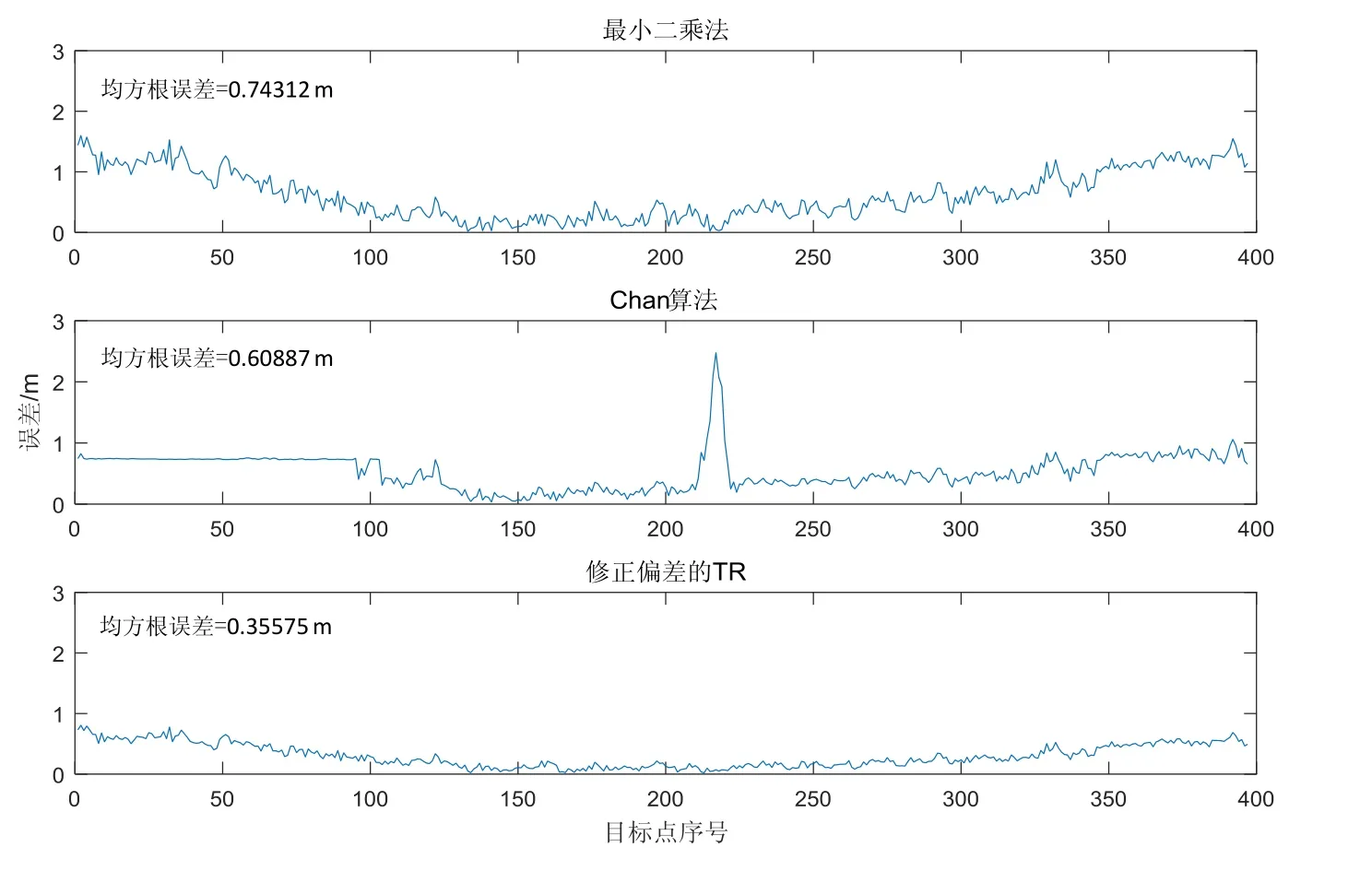
图8 定位误差效果对比Fig.8 Comparison on positioning error effects

4 结 论

在室内环境中利用UWB进行三维定位易受基站在高度方向布置限制的影响，使得该方向的定位误差较大。本文提出一种二次解析方法以提高高度方向的定位效果和整体定位效果。首先采用传统方法对目标点进行定位，获取目标点位置的一次解析值，然后使用修正偏差的 Tikhonov正则化方法再次对目标点位置进行估计，以提高高度方向定位精度。该方法能有效地提高高度方向的定位精度和整体定位精度。

从仿真分析与实验结果来看，本文提出的算法能够将传统解析法的定位精度提高40%以上，能够显著提高基站在某个方向具有布置限制时该方向的定位精度。其中实验结果表明，所提方法的定位效果比最小二乘法提高52.1%，比Chan算法提高41.6%。由于本方法采用的依然是基于解析法的算法，故其计算相比于传统解析法只多一次判断和一次解析时间，相比于Kalman滤波算法等没有滞后效果，而且同样可以作为其他方法的解算初值。