硅微谐振加速度计的模态分析与实验
张秀丽,何晓飞,,尹永刚,方政翔,韩丰田
(1.北京交通大学 机械与电子控制工程学院,北京 100044;2.清华大学 精密仪器系,北京 100084)
硅微谐振加速度计因其精度高、体积小、功耗低以及能够实现准数字化输出的特点[1],成为国内外高性能微机电加速度计的研究热点之一。美国Draper实验室是最早研制成功硅微谐振加速度计的单位之一,报道的样机性能已达到战略级精度水平[2]。国内从21世纪初开始对硅微谐振加速度计开展了持续研究[3-6],报道的样机性能已展现出高精度的潜力。
目前,与硅微谐振加速度计结构相关的文献中,研究重点是低温漂、高灵敏度器件结构的设计及参数优化,噪声分析以及样机的性能测试结果等,对其结构设计中谐振器振动模态的选取及其理论依据均提及较少或未提及。有少部分文献曾介绍过硅微谐振加速度计的振动模态[7],但仅是进行了概述或仿真分析,还缺乏对不同振动模态下的加速度计性能进行深入的分析比较和实验验证。在结构设计时,谐振器振动模态的选取是设计者需要考虑的关键因素之一。选取的振动模态不同,谐振器所呈现的振动特性也不同[8-9]。
本文采用理论建模、仿真分析以及实验验证的方法,对比分析了一种典型的硅微谐振加速度计结构在不同振动模态下所呈现出的特性,有助于指导硅微谐振加速度计的敏感结构与驱动方案设计。
1 模态分析
典型的硅微谐振加速度计是由两部分完全相同的对称结构构成,其工作原理为:当外界沿敏感轴方向(x轴)有加速度输入时,一侧结构中的谐振器受拉力而使谐振频率增加,另一侧结构中的谐振器受压力而使谐振频率减小,通过测量两个谐振频率的差值可反映外界输入加速度的大小和极性。图1给出了沿y轴对称的加速度计结构中的右侧结构示意图。
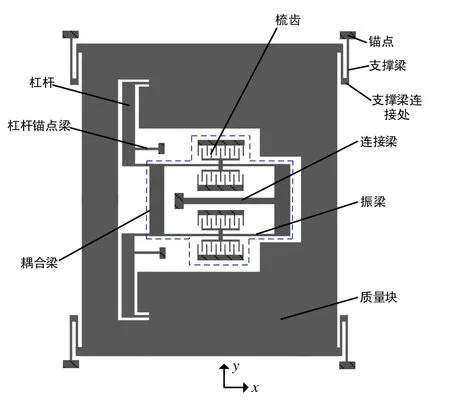
图1 谐振加速度计结构示意图Fig.1 Schematic of the resonant accelerometer structure
图1中蓝色虚线框内为谐振器,谐振器由耦合梁、振梁、连接梁、梳齿组成。其中上下两根振梁通过耦合梁连接,与振梁相比,耦合梁的梁宽大、长度小,设计的耦合梁刚度远大于振梁刚度,可将其视为刚体。因此,谐振器沿竖直方向(y轴)可简化为三自由度振动模型,如图2所示。
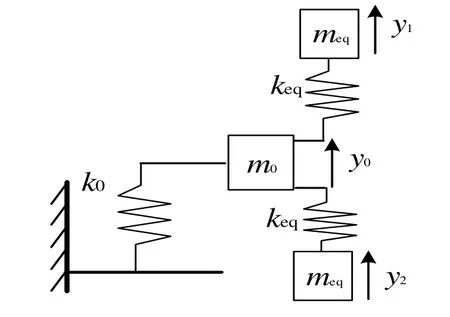
图2 谐振器简化振动模型Fig.2 Simplified vibration model of the resonator
对图2模型使用刚度法建立运动微分方程如下:
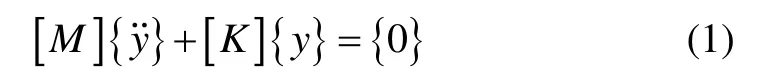
式中,
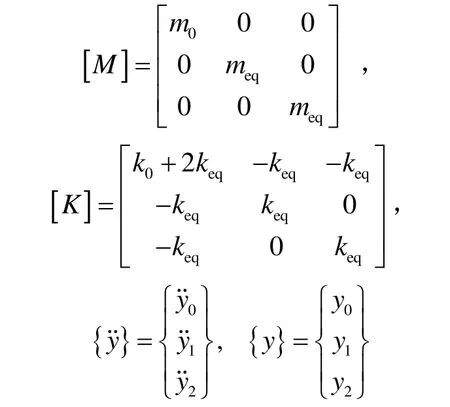
m0为连接梁和耦合梁的等效质量,meq为振梁的等效质量,k0为连接梁和耦合梁在竖直方向上的等效刚度,keq为振梁的等效刚度,和y分别为谐振器振动时的加速度矢量和位移矢量。
驱动振梁做简谐运动时,其运动方程为:
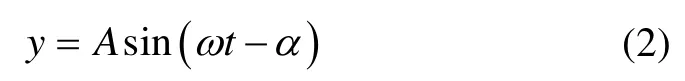
由式(1)(2)解得上述谐振器模型的特征频率为:
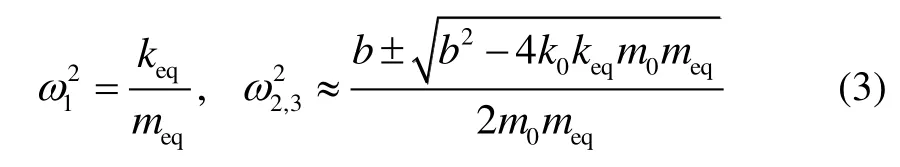
式中,b=k0meq+keqm0+2keqmeqarcsinθ。
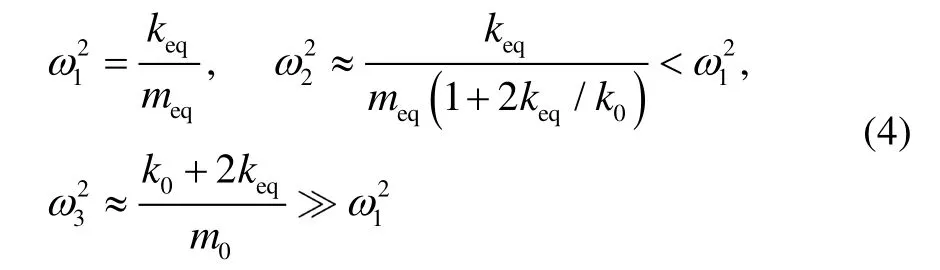
从式(4)可看出,谐振器简谐振动时,系统有三个主要模态,其中:ω1为振梁的特征频率,对应反相振动模态,其振型如图3(a)所示;ω2略小于ω1对应同相振动模态,其振型如图3(b)所示;ω3远大于振梁特征频率,其振型不唯一。当谐振器尺寸变化时,ω3的振型随之变化,故不可作为硅微谐振加速度计结构设计时的选用模态。同相和反相振动模态均能够以特定的振型来反映谐振器的振动情况,可以作为结构设计时的选用模态,因此下面对其进行重点分析。
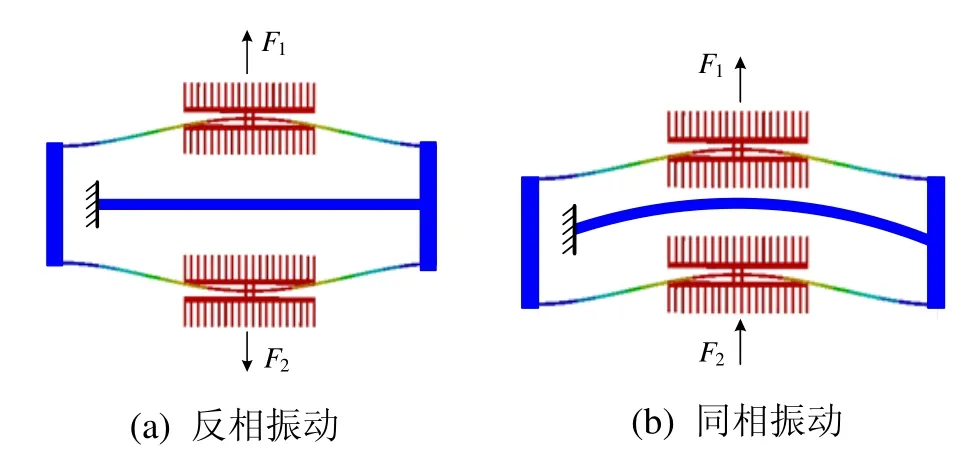
图3 反相和同相振动模态示意图Fig.3 Schematic of anti-phase and in-phase vibration modes
当振梁被施加x轴向力F时,振梁在同相模态和反相振动模态下的角频率如下:
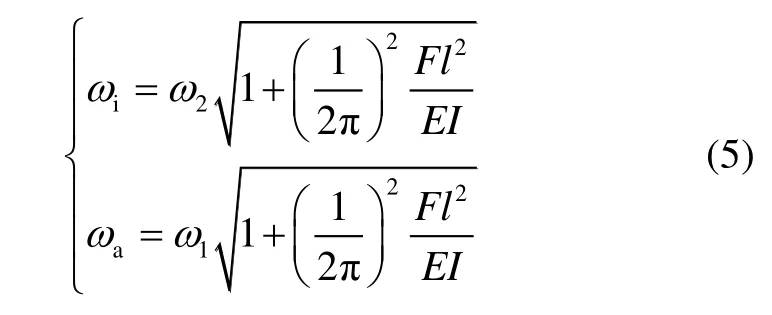
将式(5)进行泰勒展开并忽略高阶项后,可得两种模态所对应的谐振频率:
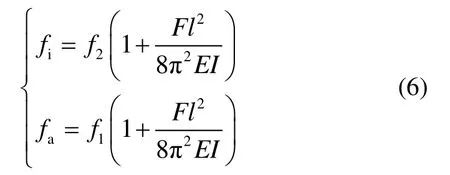
将F=Mg代入式(6),即可分别得出两种模态所对应加速度计的标度因数。标度因数是硅微谐振加速度计结构设计时需考虑的关键性能之一,将两模态对应的标度因数作差,可得到同一个硅微谐振加速度计在不同工作模态下的标度因数差值与谐振频率差值间的关系模型:
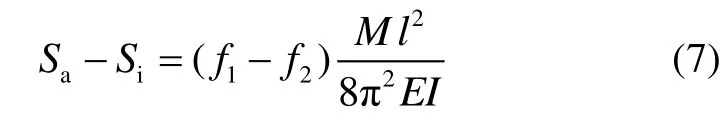
其中,S为标度因数,M为检测质量块的质量,E为硅的杨氏模量,I为振梁的转动惯量。从式(7)中可以看出,对于同一硅微谐振加速度计,其同相模态和反相模态所对应标度因数的差值与谐振频率的差值呈线性关系。对同一硅微谐振加速度计结构,其M、E、I为定值,通过改变连接梁梁宽来改变两种模态谐振频率间的差值进行ANSYS仿真,可以得到两模态所对应标度因数差值与谐振频率差值间的关系,如图4所示。
显见,图4中两个模态下的标度因数间差值与谐振频率间差值近似为线性关系,与式(7)的模型预测基本一致。
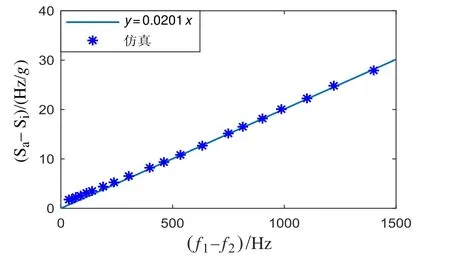
图4 仿真的标度因数差值随谐振频率差值变化Fig.4 Simulated scale factor varies with the difference of resonant frequency
2 能量分布分析与实验
当谐振器在同相模态振动时,如图3(b)所示,两根振梁的振动方向相同,谐振时振梁的振动幅值较大,对质量块施加有力的作用,使检测质量在竖直方向上运动,从而分担部分振动能量。因此,同相模态振动时能量分布主要包括振梁振动、阻尼消耗、质量块运动三个部分。
谐振器反相模态振动如图3(a)所示,两根振梁振动方向相反,作用于质量块上的力相互抵消,由于检测质量不产生相对运动,故不分担能量。此时,系统能量分布主要有两方面,即振梁振动和阻尼消耗两部分。
对于微机电加速度计而言,阻尼消耗能量的大小主要受真空度制约[10],而用于实验的样机真空度目前已经达到较高水平(小于0.1 Pa)。因此,阻尼消耗的能量极小,可认为一个振动周期内两种振动模态下阻尼消耗的能量差别不大。
两种振动模态下,单根振梁振动一个周期所存储的能量可表示为:
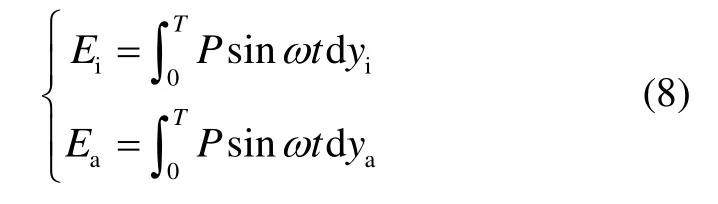
其中,T为振梁振动周期,Psinωt为静电激励力,yi和ya分别为同相与反相振动模态下振梁的振动位移。
在图1所示结构中,当振梁谐振时,质量块在竖直方向的振幅主要受三部分刚度影响,即杠杆锚点梁弯曲刚度,连接梁弯曲刚度以及支撑梁沿竖直方向的刚度。三部分的刚度计算公式如下:
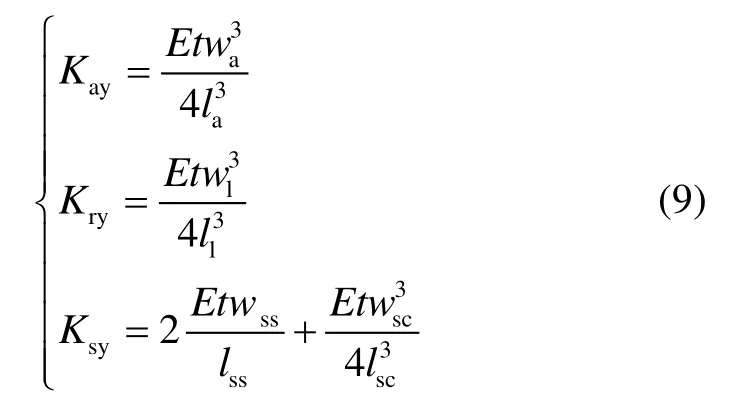
式中,t为结构厚度,wa和la分别为杠杆锚点梁宽度和长度,wl和ll分别为连接梁宽度和长度,wss和lss分别为支撑梁宽度和长度,wsc和lsc分别为支撑梁连接处宽度和长度。
得到三部分共同作用下的总刚度为:
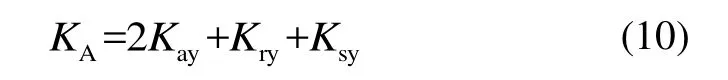
两根振梁在谐振状态下对检测质量施加的合力为:

检测质量等效的位移为:

检测质量振动一个周期所需能量为:

硅微谐振加速度计的品质因数Q表示一个振动周期内,谐振器存储能量与消耗能量的比值。同一结构在两种振动模态下,阻尼消耗的能量基本相同,当输入驱动电压相同即提供相同的能量时,两种振动模态下,品质因数与振梁振动一个周期所存储能量间的关系应满足下式:

由式(8)(14)可以得到相同驱动力下,两种振动模态的品质因数与振梁振幅之间的关系如下:

即同一硅微谐振加速度计在同相、反相两种振动模态下,品质因数比值等于振梁振动位移比值。
从能量分布来看,同相振动模态下引起检测质量振动会分担部分能量,在外界供能相同的情况下,同相振动模态下振梁振动幅值应小于反相振动模态下的振梁振动幅值,且两振动模态下能量分布满足下式:
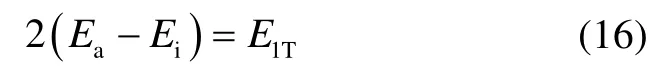
即检测质量振动一个周期所分担能量的大小等于两振动模态下两根振梁振动一个周期所存储能量的差值。
为了验证上述结论,对所设计的硅微谐振加速度计结构在相同驱动力下进行模态仿真和实验研究。将同一加速度计样机分别连接在同相模态和反相模态稳幅控制电路中,设定相同的驱动电压,利用动态信号分析仪在谐振频率附近(1 Hz范围内)进行开环扫频测试。将扫频数据转换为振梁振幅,得到两种模态下的实验曲线。将该驱动电压转换为等效静电力后,用ANSYS软件在样机结构谐振频率附近(1 Hz范围内)进行频率-振幅分析。通过仿真和实验得到两种模态下振梁振幅如图5所示。
由图5可以看出,同相振动模态下振梁振幅最大值的仿真值和实验值分别为4.07×10-2μm和3.92×10-2μm,反相振动模态下振梁最大振幅分别为 8.2×10-2μm 和7.86×10-2μm,将其代入式(8)(13)中可以得到两振动模态下各部分能量的仿真值和实验值,如表1所示。
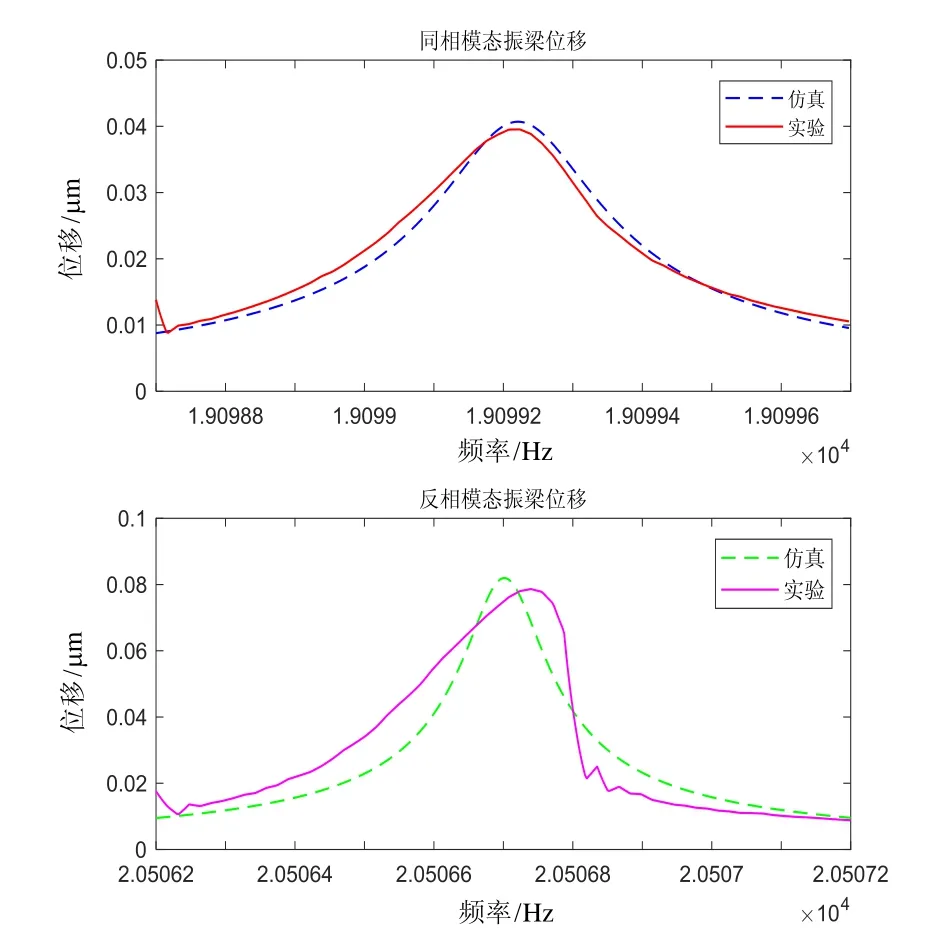
图5 两种模态下的振梁振幅比较Fig.5 Comparison on vibration amplitudes of resonant beams operating at two modes

表1 两种振动模态下各部分能量的仿真和实验结果Tab.1 Simulated and experimental energy for two vibration modes
由表1可以看出,各部分能量的仿真值和实验值具有较好的一致性,根据式(16),检测质量振动一个周期所分担能量的大小应等于两振动模态下两根振梁振动一个周期所存储能量的差值,而从表中数据可以看出两者具有3.5%的差异,分析表明二者的差异主要来源于工艺误差导致刚度计算用的设计参数与样机实际结构参数不完全一致。
3 噪声分析与实验
加速度计的频率噪声主要由三部分组成,即非线性振动噪声fn1、频率测量噪声fn2以及与振幅无关的噪声fn3。噪声计算公式如下[11]:
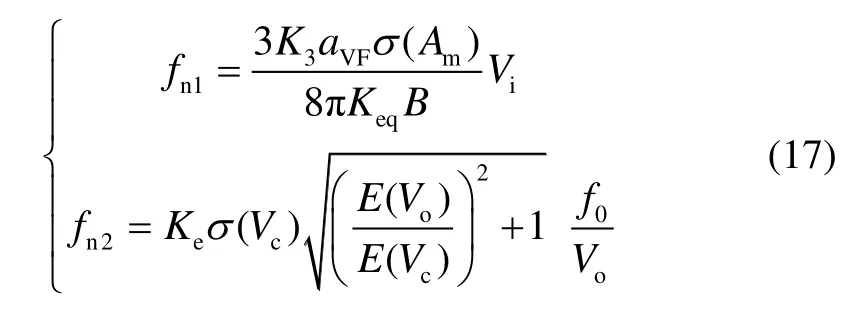
其中,K3为非线性刚度系数,σ(Am)为闭环后振幅的标准差,aVF为输入电压与驱动力之间的转换系数,B为阻尼系数,Vi为输入驱动电压,E(Vc)为实验仪器本身的测量噪声,E(Vo)为输出信号噪声功率谱密度,Keσ(Vc)为与频率计相关参数。
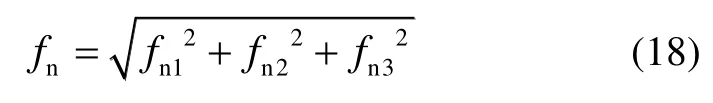
总体噪声可表示为:式中,fn3包括机械热噪声、仪器噪声、地基噪声以及谐振时结构产生不稳定振动引起的噪声。由于两种振动模态实验均在相同环境条件下进行,且采用同一套实验设备,因此两种振动模态下,fn3的主要区别在于谐振时结构产生不稳定振动引起的噪声。
通过实验对相关参数进行测试和计算,得到驱动电压幅值在36 mV时两种振动模态的各个噪声分量及总噪声的理论值如表2所示。
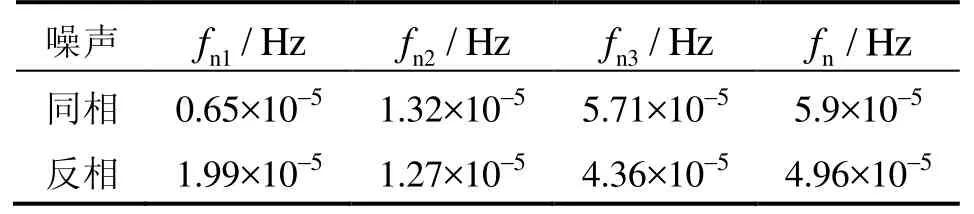
表2 各类噪声分析结果Tab.2 The analysis results of various noises
从表2中可以看出,两种振动模态在相同驱动电压下噪声的主要区别在于非线性振动噪声以及与振幅无关的噪声。
为了研究两种振动模态下,驱动电压幅值对非线性振动的影响,将同一样机在两种振动模态下采用不同驱动电压进行开环扫频实验,两种振动模态下的实验结果如图6所示。
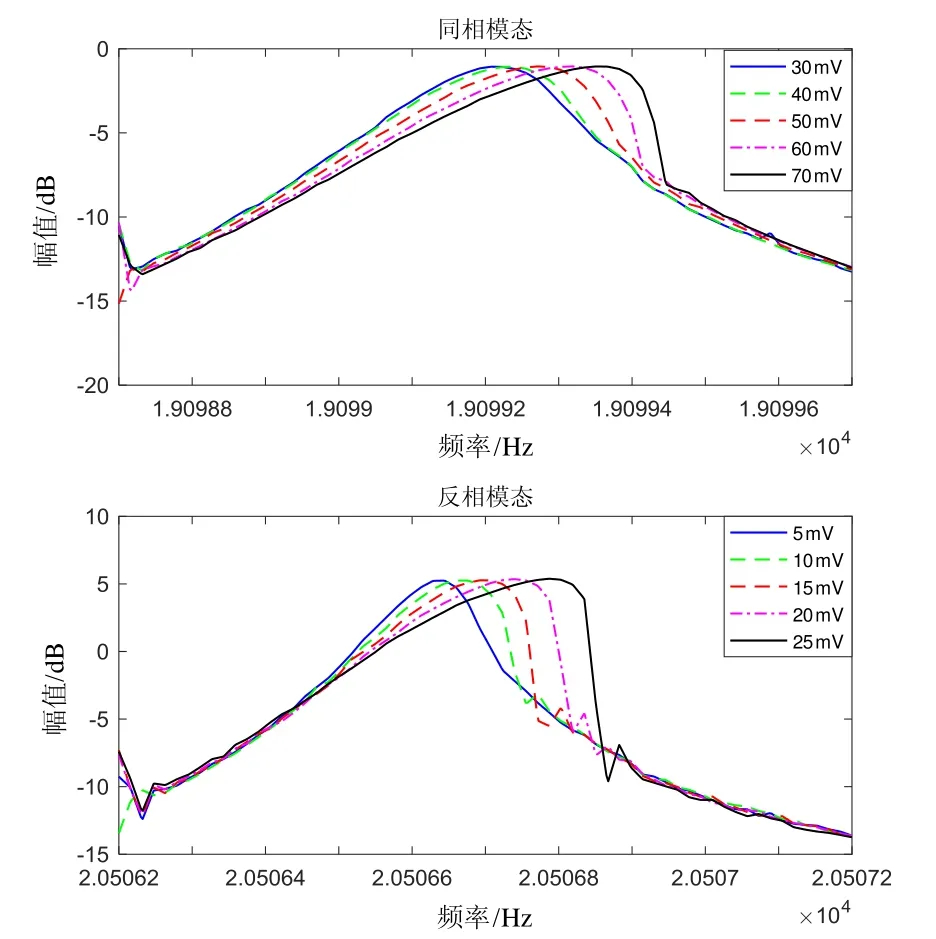
图6 不同驱动电压下的振动非线性实验结果Fig.6 Nonlinear vibration responses with different driving voltage settings
从图6可以看出,同相振动模态在驱动电压为60 mV附近时出现明显的振动非线性,而反相振动模态在驱动电压为10 mV附近时就开始出现明显的非线性。因此,当驱动电压为36 mV时,同相振动模态仍处于线性振动区域,非线性振动噪声对总体噪声的影响较小,而反相模态已处于非线性振动区域,其非线性振动引起的噪声影响较大。
同相振动模态下与振幅无关的噪声相比于反相振动模态较大,其原因在于谐振在同相振动模态下,如第2节所述振梁的振动会引起检测质量块的位移从而导致结构产生不稳定振动使噪声增大。
当驱动电压设为36 mV时,对样机进行闭环稳幅并进行了噪声测试,总测试时间为1 h,取测试开始半小时后的1800个点,每60个点计算一次标准差作为噪声,可以测得两振动模态下的噪声如图7所示。
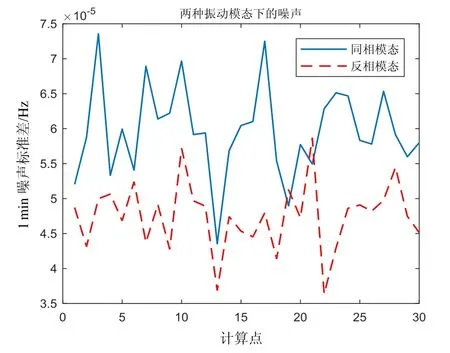
图7 两种振动模态下的频率噪声Fig.7 The measured frequency noises in two vibration modes
由图7可以看出,同相振动模态下的实测频率噪声均值为5.97×10-5Hz,反相振动模态下的实测频率噪声均值降低至4.75×10-5Hz,与理论计算值相近。
4 实验结果
总结同相振动模态和反相振动模态下的样机实验结果如表3所示。
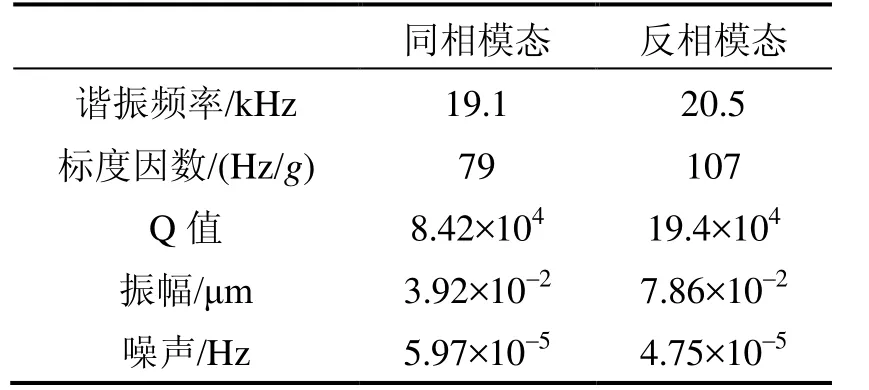
表3 两种振动模态下的样机实验测试结果对比Tab.3 Comparison on experimental results of the MRA prototype in two vibration modes
5 结 论
本文对硅微谐振加速度计工作在两种不同振动模态时,其关键性能参数进行了分析比较与实验验证,为硅微谐振加速度计设计人员确定振动模态提供了参考依据。结果表明:同相和反相两种振动模态均可以用于检测输入加速度,两者标度因数的差别与所设计谐振频率的差别呈线性相关关系,样机实验及仿真结果中当反相模态谐振频率与同相模态谐振频率相差 1.4×103Hz时,两者标度因数相差28 Hz/g;当无外界加速度输入时,同相模态振动会引起检测质量运动而消耗更多能量,导致振梁振动的位移幅值减小,品质因数下降,也正是由于检测质量的运动消耗能量,导致同相振动模态下谐振器的线性振动区较反相振动模态更宽,非线性噪声更小,但检测质量的运动也会产生不稳定的振动噪声,从而使同相振动模态下的总体噪声略大于反相振动模态。本实验结果中同相模态的总体噪声为5.97×10-5Hz,反相模态总体噪声低至4.75×10-5Hz。

