基于微孔参数优化的超流体陀螺噪声抑制方法

郑 睿，余 童，程龙阅

（1.安徽师范大学 物理与电子信息学院，芜湖 241002；2.安徽省智能机器人信息融合与控制工程实验室，芜湖 241000）

陀螺仪的精度直接影响惯性导航系统的精度[1-3]。基于萨格纳克干涉效应，物质波干涉式陀螺仪是新型的超高精度的陀螺仪[4-5]。超流体陀螺是物质波干涉式陀螺仪的一种，其测量精度预期可达10-10rad/(s⋅Hz1/2)的数量级，将来可以应用于航天、宇航、深海探测等领域[6-9]。

陀螺仪的精度与其噪声有密切相关的联系。研究表明，在不考虑环境干扰的情况下，超流体陀螺内部存在热能量、薄膜位移检测系统的误差等噪声源，引起其输出端产生数量级为 10-8～10-7rad/(s⋅Hz1/2)的近似白噪声[10]，这严重影响了超流体陀螺的测量精度，因此需要开展超流体陀螺噪声抑制的方法研究。

超流体物质波是基于超流体在弱连接处发生约瑟夫森效应而产生的。因而在超流体陀螺的结构中，存在很多的微孔组成的微孔阵列，这也被称为弱连接。Sato等[11]在实验中发现，随着微孔孔径、微孔数量等参数的变化，超流体陀螺的噪声也发生了变化。由此可以表明改变微孔参数可以抑制超流体陀螺的噪声。但是，当前对于该问题的认识仍处于实验阶段，微孔参数与超流体陀螺噪声之间的数学模型尚不清楚[6]。

本文在分析了超流体陀螺噪声的基础上，构建微孔参数与超流体陀螺噪声之间的数学模型，提出基于微孔参数优化的超流体陀螺噪声抑制方法，从改变陀螺结构参数的角度对其噪声进行抑制，从而挖掘超流体陀螺高测量精度的潜力。

1 超流体陀螺的噪声分析

超流体陀螺的结构如图1所示，是由图中虚线内的超流体干涉仪、温度控制系统、化学势能差驱动系统、位移检测系统、幅值控制系统构成的。其中超流体干涉仪是敏感角速度的核心部件，其它是辅助超流体干涉仪工作系统。

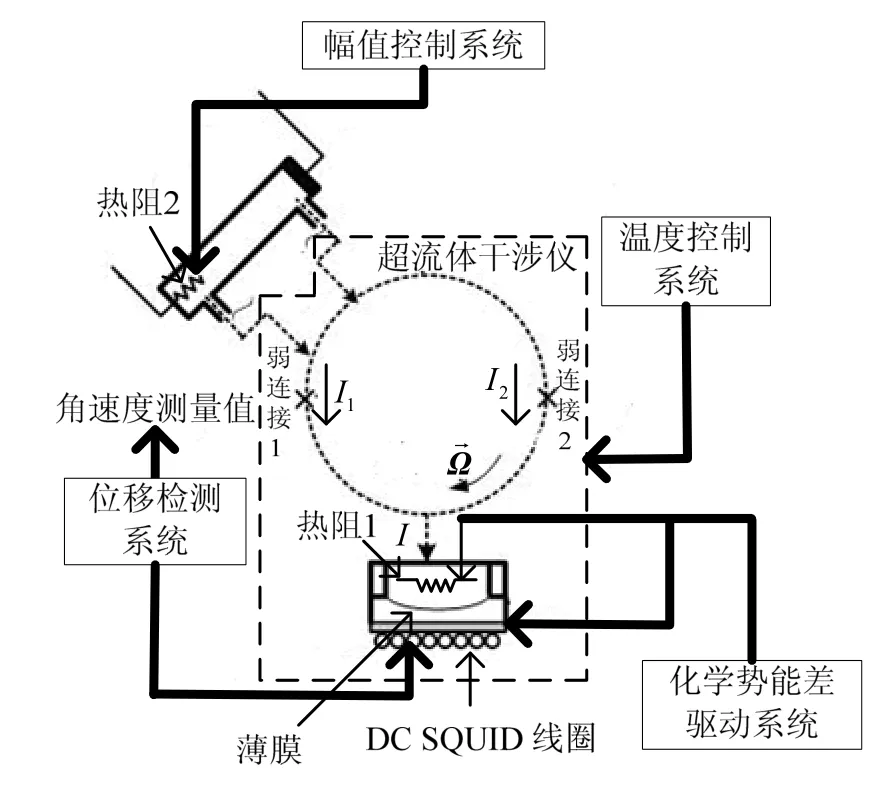
图1 超流体陀螺结构图Fig.1 Structure of superfluid gyroscope

图1中，超流体干涉仪中虚线所示的环形腔内充满超流体4He，“×”的位置表示数千个微孔组成的阵列，当微孔孔径d满足如式(1)所示的关系时为弱连接[6]。

式中，4ξ表示弱连接的临界孔径，T表示当前温度，λT≈2.1716K表示超流体4He的临界温度。利用热阻1加热，弱连接两侧产生温度差和压力差，由此产生化学势能差。在化学势能差的作用下，超流体在弱连接处发生约瑟夫森效应，产生两路超流体物质波（若微孔孔径d不满足式(1)，此时微孔阵列是强连接，则不能在化学势能差的作用下发生约瑟夫森效应）。这两路物质波可以表示为：

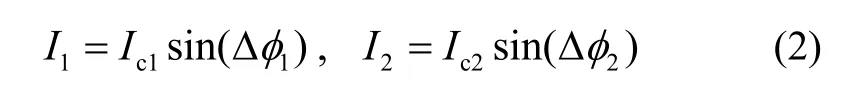
式中，I1和I2为流过1号弱连接和2号弱连接的超流体的质量流量，Ic1和Ic2分别为I1和I2的幅值，Δφ1和Δφ2表示两个弱连接两侧的相位差。

根据图1可以看出，总流量I是I1和I2的叠加，因此总流量将同样以正弦变化，其幅值Im为[6]：

式中，Δφe= Δφ1- Δφ2表示超流体相移，它由萨格纳克相移Δφs（角速度矢量 引起）和热相移Δφh（热阻2的加热引起）共同组成[6]：

由式(3)(4)可知，外界角速度变化会引起超流体相移变化，从而使得超流体流量变化。因此检测超流体流量即可测量角速度，这就是超流体陀螺测量角速度的原理。由于超流体的约瑟夫森效应会引起薄膜位移变化，因此薄膜位移也呈现正弦变化，其幅值xm为：

式中，fJ为约瑟夫森频率，ρ为超流体密度，Ad为薄膜表面积。

根据文献[10]的研究，热能量、温度控制系统的输出波动、化学势能差驱动系统的输出波动、幅值控制系统的误差、位移检测系统的噪声是超流体陀螺噪声的主要来源。而对超流体陀螺影响最大的是位移检测系统的噪声，因此位移检测系统的噪声被视为超流体陀螺的主要噪声源。

设位移检测系统噪声为δxmn，由式(4)和式(5)可知，角速度测量值Ωd与xm之间存在着非线性关系，利用非线性随机变量方差的求解方法，由δxmn引起dΩ的噪声Ωdn为：

由式(4)(6)可得，超流体陀螺的噪声Ωdn为：

根据通用的参数[10]，超流体陀螺的噪声为10-8～10-7rad/(s⋅Hz1/2)的数量级。超流体陀螺预期的测量精度是可以达到10-10rad/(s⋅Hz1/2)数量级的。因此输出噪声较高，使得其高测量精度的潜力不能发挥，这是超流体陀螺需解决的主要问题。

2 微孔参数与超流体陀螺噪声之间的数学模型

图2 弱连接处微孔阵列的示意图Fig.2 Aperture arrays at the weak link

由图2可以看出，微孔孔径越大、微孔数量越多，就可使得Ic越大，从而抑制超流体陀螺噪声。但由于微孔参数与超流体陀螺噪声之间的定量关系还不清楚，因此本文首先研究微孔孔径d以及微孔数量N与超流体流量幅值Ic的关系，构建微孔参数与超流体陀螺噪声之间的数学模型，在此基础上进一步研究抑制的效果。

2.1 微孔孔径与微孔流量幅值之间的关系

由于超流体流过单一微孔的速度幅值vc为[6]：

式中，κ4=h/m4，h是普朗克常数，m4是4He原子质量。那么流过单一微孔的超流体质量流量幅值Ic0为：

式中，ρs表示超流体中超流性成分的密度，a表示微孔面积。式(9)表示出微孔孔径与微孔流量幅值之间的关系。

为了使得Ic变大，单一微孔中的Ic0也应该变大，由式(9)可知，微孔孔径d应取最大值。由式(1)可知，d的最大值dmax=ξ4。把微孔孔径用其最大值代替，由式(9)可得：

式(10)表明，当微孔孔径取最大值时，可以使得Ic0达到最大值。

2.2 微孔数量与微孔流量幅值之间的关系

在弱连接两侧存在化学势能差的情况下，超流体在弱连接处的每个微孔处发生约瑟夫森效应：

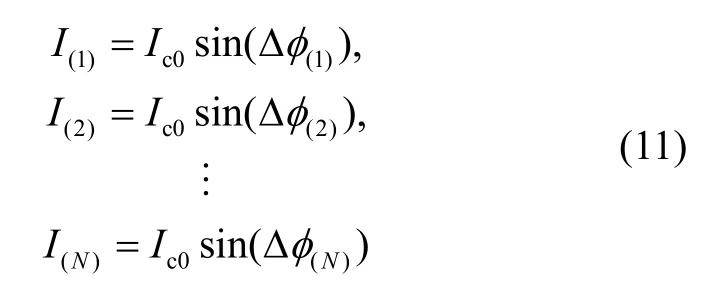
式中，I(1),I(2),…,I(N)表示流过1号微孔、2号微孔、N号微孔的超流体的质量流量；Δφ(1),Δφ(2),…,Δφ(N)表示每个微孔两侧的超流体相位差。

由图2可知，流过1号弱连接的流量I1是由流过所有微孔的流量之和，即

但在超流体陀螺中，热噪声始终存在。受到热噪声影响，Δφ(1),Δφ(2),…,Δφ(N)上面叠加了白噪声，因此它们是相互独立的随机变量。为精确研究Ic与N的关系，必须考虑热噪声的影响。

因此利用复数表示式(12)中各正弦量，比如，Icsin(Δφ)表示为Ic∠Δφ，Ic0sin(Δφ(1))表示为那么式(12)的复数形式为：

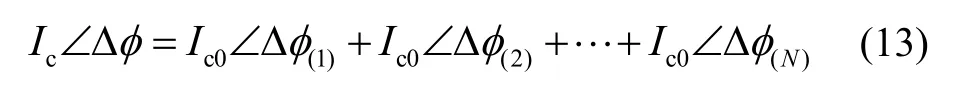
根据复数的运算知识，式(13)等号左边复数的模为Ic，为计算式(13)等号右边所描述的复数的模，对式(13)等号右边所描述的复数采用代数式表示：

式中，j表示复数算子(j2=-1)。式(13)等号左右两边的复数的模应相等，因此由式(14)可得：

式(16)表示微孔数量与Ic之间的关系。由式(16)可以看出，Ic随着N的增大而增大。

2.3 微孔参数与陀螺噪声之间数学模型的构建

基于上述研究，把式(9)(16)代入式(7)可得，超流体陀螺噪声与微孔孔径、微孔数量之间的关系为：

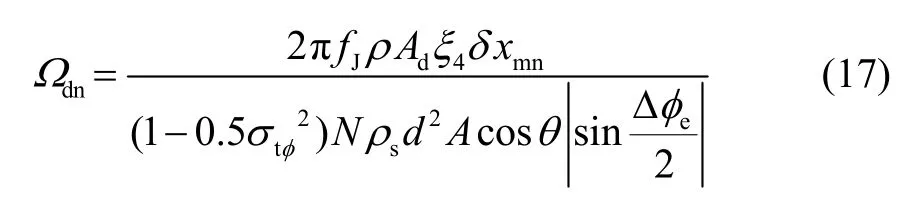
由式(17)可知，随着微孔孔径和微孔数量的增加，超流体陀螺输出噪声将逐渐减少，因此增大微孔孔径和微孔数量对超流体陀螺的噪声有抑制效果。

根据式(10)可知，微孔孔径的最优值是其最大值ξ4。由于超流体陀螺的管路受到尺寸的限制[12]，因此微孔数量也是要受到限制的，设其最优值也是其最大值，设为Nmax。把微孔阵列参数的最优值代入式(17)，可得此时超流体陀螺的噪声达到最小值Ωdn(min)为：

式(18)是微孔阵列参数取最优值时，超流体陀螺噪声的数学模型。

3 仿真与分析

为验证基于微孔参数优化的超流体陀螺噪声抑制方法的有效性，利用超流体陀螺仿真实验平台，开展实验与分析。首先分析微孔参数的变化范围，研究在微孔参数的变化范围陀螺噪声的变化规律；接着选择输入为典型的角速度，在取通用微孔参数和最优微孔参数两种情况下，分别对角速度测量值误差进行分析。

3.1 仿真实验平台

超流体陀螺仿真实验平台的结构如图3所示。在该实验平台中，基于大量的实验数据，在计算机上模拟超流体干涉仪的工作过程，这部分的主要环节包括热驱动模块、热相移输入模块、角速度敏感模块和薄膜位移产生模块等几个部分。超流体陀螺的相移控制系统则由硬件实现，包括角速度信息提取模块、高精度反馈热相移处理电路和热相移控制电路等部分。实验平台中各部分之间的关联如图3中箭头指向所示。

图3 超流体陀螺仿真实验平台结构框图Fig.3 Structure of superfluid gyroscope simulation experimental platform

3.2 微孔参数变化范围内噪声的变化规律

基于上述实验平台，实验的基本参数设置为：

① 微孔孔径[6]：取工作温度为T=2.1712K，根据式(1)可知在该温度下dmax=95 nm。另外，由于微孔孔径最小可以为 50 nm，因此设置微孔孔径的变化范围为50 nm到95 nm。

② 微孔数量：弱连接处的微孔必须大于一定数量，否则流过弱连接的超流体流量较少，使得薄膜位移过小而无法被检测到。当前微孔数量最小为 2500个。受到超流体管路尺寸的限制，微孔的数量也不能很大，当前报道的微孔数量最多为5625个[6]。

除了微孔参数，其它相关参数设置为：

③ 结构参数[6]：超流体管路半径Rc=2×10-2m,θ= 0，薄膜面积为Ad=5×10-5m2。

④ 工作参数[6]：工作温度为T=2.1712K，约瑟夫森频率为fJ=1000 Hz，超流体相移Δφe的锁定值设置为π/2，系统的测量带宽为1000 Hz。

⑤ 噪声源[10]：位移检测系统噪声δxmn=10-15m/Hz1/2；

基于上述参数，根据式(17)可得在微孔孔径和微孔数量的变化范围内，超流体陀螺的噪声变化规律如图4所示。

由图4可以看出，随着微孔数量由2500增加到5625，微孔孔径由50 nm增加到95 nm，超流体陀螺的噪声从超流体陀螺的噪声由6.3×10-7rad/(s⋅Hz1/2)逐渐减小为7.7×10-8rad/(s⋅Hz1/2)，因此超流体陀螺的噪声呈现逐渐下降的趋势。由此表明增大微孔孔径和增加微孔数量可以有效抑制超流体陀螺噪声。因此为抑制超流体噪声，微孔孔径和微孔数量应尽可能取较大的值。

图4 微孔阵列参数对超流体噪声的影响曲线Fig.4 Curve of Influence on superfluid gyroscope noise with aperture array parameters

3.3 两种典型输入角速度情况下噪声的抑制效果

为进一步研究微孔阵列对超流体陀螺噪声的抑制效果，在两种典型输入角速度情况下，取通用微孔参数和最优微孔参数，观察超流体陀螺的噪声情况。实验参数设置为：

① 通用微孔参数：根据3.2节的研究可知，微孔孔径的变化范围为50 nm到95 nm微孔数量的变化范围为2500到5625。在国内外的研究中，最为常见的一组参数是：微孔孔径为70 nm，微孔数量为4225，如文献[8]、文献[10]和文献[11]都选择的是这组数值，因此本文把这组参数称为通用微孔参数。微孔孔径为70 nm，微孔数量为4225；

② 最优微孔参数：根据上文分析可知，微孔孔径取最大值95 nm，微孔数量取最大值5625，这时的微孔参数达到最优；

③ 输入角速度Ω设置为两种典型的类型：第一种是恒定角速度，Ω=2×10-6rad/s；第二种是正弦输入，Ω=2×10-5sin(2πt) rad/s。仿真时间为 1 s。

④ 其它参数同3.2节中的设置。

根据上述参数模拟超流体陀螺的工作过程，可得两种典型输入角速度情况下角速度测量值、角速度测量值的误差如图5～8所示。

由图5可知，角速度恒定的情况下：超流体陀螺输出的角速度测量值存在随机波动的噪声。而取最优微孔参数时，噪声波动的幅度要小于取通用微孔参数时。进一步由图6中的数据精确分析可知，取通用微孔参数时，角速度测量值误差的标准偏差为5.7×10-8rad/(s⋅Hz1/2)，由于统计时间是 1s，此时超流体陀螺的噪声是5.7×10-8rad/(s⋅Hz1/2)；取最优微孔阵列参数时，角速度测量值误差的标准偏差为 2.8×10-8rad/(s⋅Hz1/2)，在1 s的统计时间下，超流体陀螺的噪声为 2.8×10-8rad/(s⋅Hz1/2)，是取通用微孔阵列参数时的约1/2。

图5 角速度测量值（角速度恒定）Fig.5 Curve of superfluid gyroscope detecting value(the angular velocity is constant)

图6 角速度测量值的误差（角速度恒定）Fig.6 Curve of superfluid gyroscope detecting value error (the angular velocity is constant)

由图7可知，角速度正弦变化的情况下，超流体陀螺输出的角速度测量值在正弦变化的基础上叠加了随机噪声。同样，取最优微孔参数时，噪声波动的幅度要小于取通用微孔参数时。由图8中的数据分析可知，由于此时的角速度是时变的，通过超流体陀螺仿真实验平台的解算，角速度测量值误差的标准偏差比测量恒定角速度时要大一些，约为9.2×10-8rad/(s⋅Hz1/2)。在1 s的统计时间里，超流体陀螺的噪声为 9.2×10-8rad/(s⋅Hz1/2)。采用最优微孔阵列参数，角速度测量值误差的标准偏差约为4.7×10-8rad/(s⋅Hz1/2)。在1 s的统计时间内，超流体陀螺的噪声为4.7×10-8rad/(s⋅Hz1/2)，也是取通用微孔阵列参数时的约1/2。

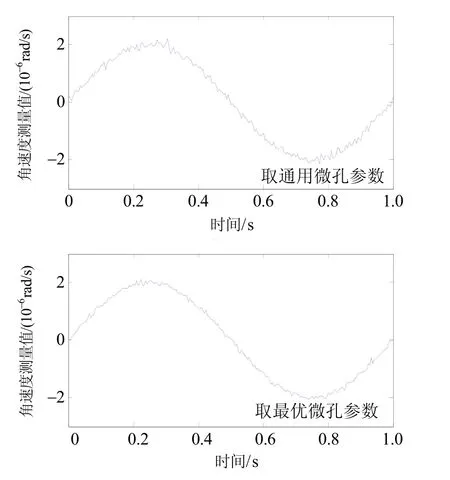
图7 角速度测量值（角速度正弦变化）Fig.7 Curve of superfluid gyroscope detecting value (the angular velocity is sinusoidal change)

图8 角速度测量值的误差（角速度正弦变化）Fig.8 Curve of superfluid gyroscope detecting value error(the angular velocity is sinusoidal change)

根据以上分析可知，采用最优微孔阵列参数，在角速度恒定和角速度时变两种典型情况下，超流体陀螺的噪声得到了有效抑制。

4 结 论

为了使得超流体陀螺能发挥其高测量精度的潜力，提出了基于微孔参数优化的超流体陀螺噪声抑制方法。由分析结果可知，随着微孔孔径和微孔数量的增加，超流体陀螺的噪声逐渐减小。

微孔孔径最大只能达到弱连接的临界孔径。受到超流体管路尺寸的限制，微孔数量也只能在一定范围之内。通过对微孔参数变化范围的研究，当前最优的阵列参数是：微孔孔径为95 nm，微孔数量为5625。基于最优微孔参数，超流体陀螺的噪声被抑制为取通用参数（微孔孔径为70 nm，微孔数量为4225）时的1/2，超流体陀螺的测量精度得到了显著提高。