基于垂直约束的深海拖曳系统USBL/DVL组合导航算法

王振杰，刘慧敏，杨慧良，贺凯飞，单 瑞

（1.中国石油大学（华东），青岛 266580；2.青岛海洋科学与技术国家实验室 海洋矿产资源评价与探测技术功能实验室，青岛 266071；3.中国地质调查局青岛海洋地质研究所，青岛 266071）

深海拖曳系统（Underwater Towed System,UTS）由母船通过长缆提供动力，广泛应用于深海科学研究以及海底调查，例如，测量海底地形测量及海底底质调查等[1]。实时高精度的动态导航定位是其进行近海底、远距离、长时间工作的重要保障[2]。常见的深海拖曳系统导航传感器包括光纤罗经、压力传感器、多普勒计程仪（Doppler Velocity Log,DVL）以及超短基线定位系统（Ultra-Short Baseline System,USBL）等，可提供运载体的姿态和方位信息、深度信息、速度信息和位置信息等。超短基线定位系统可为拖曳系统在浅水区域提供高精度位置信息，但受姿态测量精度、时延和声速误差的影响，其精度随着拖曳系统与母船的距离增加而降低。拖曳体下潜至5000 m左右的深水中时，超短基线定位系统的定位精度甚至不足10 m[2]。拖曳系统贴近海底进行工作时，多普勒计程仪可提供载体相对海底的速度信息，结合载体姿态传感器以航迹推算的方式求解地理坐标，因测速误差的影响，其位置误差随时间累积。拖曳系统在深海的工作环境复杂，单一的导航系统通常存在各种各样的局限性，需要多种传感器的导航信息密切配合。

采用RDOA（Range Difference of Arrival）模式定位的USBL定位误差随斜距增长而增加，在深海中USBL定位系统的测距精度要明显优于其定位精度[3]。校准后的压力传感器的测深精度为米级，因此可利用拖曳系统上的压力传感器测得的深度信息、USBL换能器实时吃水信息与超短基线测距信息进行耦合，以提高超短基线定位系统的水平定位精度。

为合理利用多源导航信息，常采用线性的卡尔曼滤波算法进行数据融合；对于非线性模型，则多采用基于线性近似的扩展卡尔曼滤波算法和基于确定性采样的无迹卡尔曼滤波算法[4]。本文基于自适应抗差滤波算法思想[5]和深度约束信息设计了一种适于深海拖体长时间、长距离观测的自适应抗差无迹卡尔曼滤波算法。该滤波算法可以利用深度约束信息提高滤波精度，同时通过新息向量判别定位数据中的粗差观测，提高了滤波算法的鲁棒性。

1 深海拖曳定位系统的深度传感器信息获取

如图1 所示，深海拖曳系统的导航传感器包括安装在母船的 GPS及姿态传感器和安装在拖体上的超短基线定位系统、深度计、多普勒计程仪、光纤罗经等。GPS天线可以获得母船的绝对坐标，并通过姿态传感器得到USBL换能器基阵坐标。换能器基阵使用多个（3个以上）测量单元，测量信标声信号到达各单元的时间差及声信号延迟，得到信标相对于换能器的相对坐标。

压力传感器测量拖曳系统到瞬时平均海面的垂直距离，由于其性能稳定且精度较高，可视为同GPS一样稳定可靠的导航信息源。如果拖曳系统接近海底，多普勒计程仪可以测量拖体相对海底的速度信息，结合姿态信息可得到其航迹推算位置。多普勒测速信息以及压力传感器测得的深度信息都可以有效地提高深海超短基线的定位精度。下面将详细介绍这几种导航数据的组合导航原理。

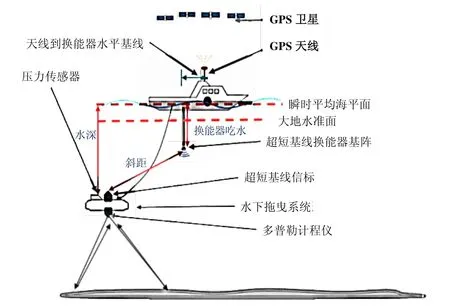
图1 基于USBL/DVL/GPS的拖曳导航系统示意图Fig.1 Deployment of USBL and geometrical relationship with GPS and DVL

1.1 无波浪影响的深度信息获取

由于海面波浪、潮汐及其他因素的影响，实时海平面在不断的变化。在浅水区，可假设由压力传感器测量得到的到海平面的垂直距离Di为[6]：

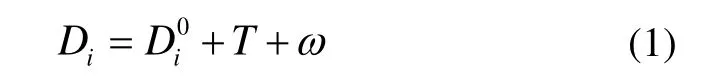
定义换能器瞬时高程为Hi可由 GPS天线求得，瞬时海面高程为Zi，且有Zi=Hi+Hd，其中，应答器的动态吃水改正为Hd。通常，潮汐的周期长达数小时，短时间内潮汐对动态吃水的高程影响可以暂不考虑。波浪的周期仅有数秒至几分钟，因而波浪对USBL换能器造成的动态吃水影响可以通过取多个历元的平均值或其他平滑算法尽量消除，此时的瞬时海面高程可表示为：

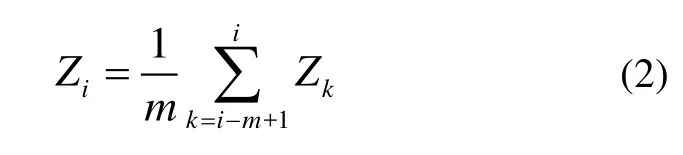
如图2(a) 所示，采用2000s的船测GPS数据，并通过姿态改正和吃水改正后得到瞬时海平面的高程。利用所有的观测数据并使用经验模态分解（Empirical Mode Decomposition,EMD）去除高频分量，并作为离线解算方案。与式(2)计算的瞬时海面高程对比，二者差距仅为数厘米。由图2(b)所知，深海中载体温盐深（Conductivity Temperature Depth,CTD）传感器测量得到的深度值比较平滑。此外 DVL测量的速度值在垂向上的积分在短时间内有较好的结果，但随着时间的累积容易发散。压力传感器可得到平滑的瞬时平均海平面，校准后精度达数厘米；而USBL换能器到瞬时平均海平面的距离可以通过式(2)粗略估计，二者之间的差值即为本文讨论的垂直约束信息。

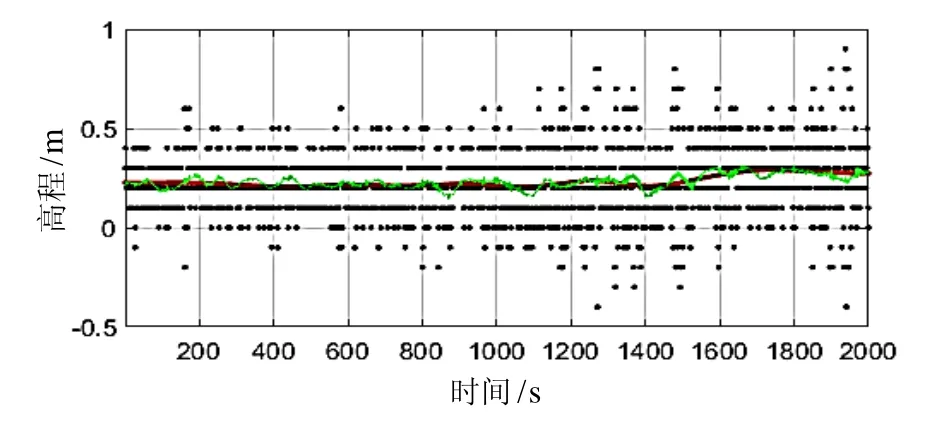
图2 (a) 换能器到大地水准面的距离Fig.2 (a) Vertical distance from USBL transducer to the mean sea level

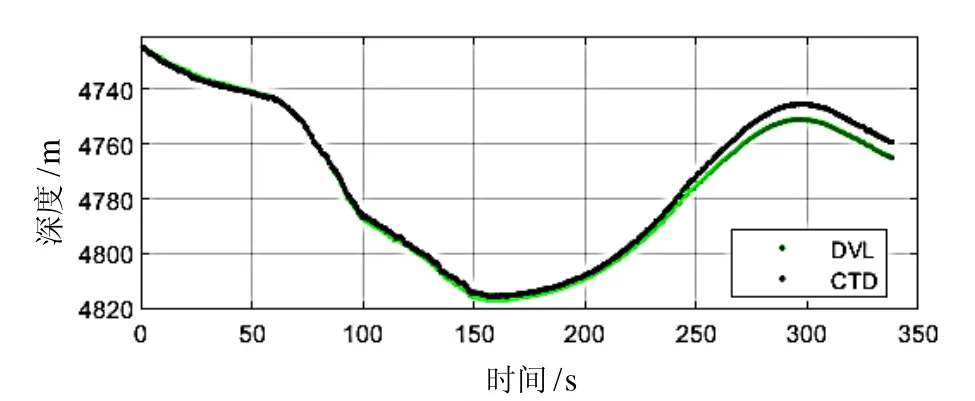
图2 (b) CTD测得及DVL垂向积分的深度Fig.2 (b) Depth from CTD and DVL

1.2 深度约束提高USBL定位精度的几何解释

超短基线定位精度多与斜距有关，USBL的测距误差精度优于米级，测角精度不够往往是水平定位误差的主因。假设其精度为 1‰～5‰，斜距为 6000 m时，USBL的定位精度为6～30 m。可结合垂直深度约束信息和高精度斜距信息给出可靠的水平约束。本节给出了二者耦合的几何原理。

为研究垂直约束对水平方向精度的影响，先不考虑测距误差对垂直约束的影响。如图3所示，在X-Z平面中，点A为换能器基阵的位置，点C和D分别为测量和真实信标位置，则由测角误差dθ引起的定位误差在X-Z平面的投影为CD，深海中其值可达数十米。此时USBL得到的高程误差值为dh，深度约束改正即将C投影到E点。易得在X-Z方向上提高的精度为CD减DE。

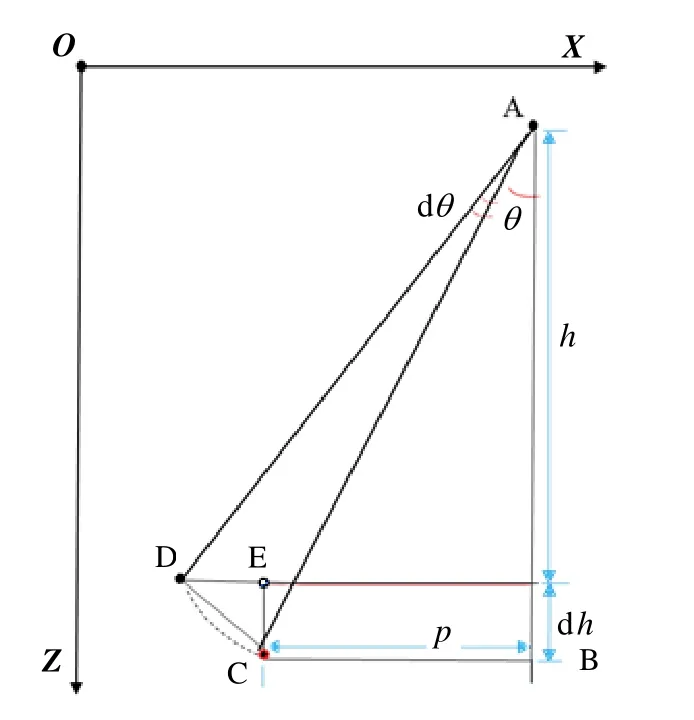
图3 垂直约束条件下超短基线信标与基阵的几何在垂直面的关系Fig.3 Geometrical relationship between USBL and target in X-Z

母船沿直线航行时，水下拖体通常在水平方向上近似沿直线运动。拖体在拖体坐标系和导航坐标系下的速度可表示为

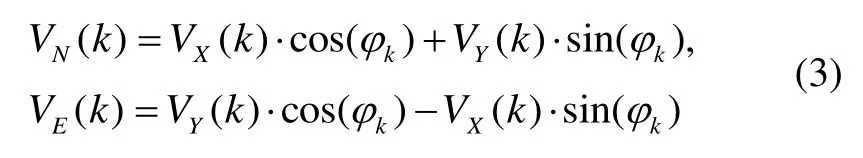
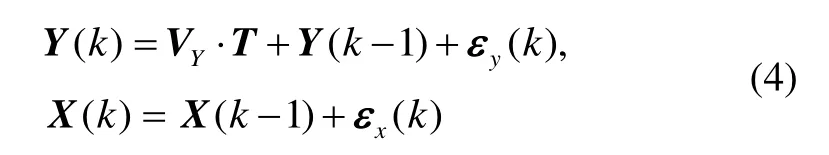
其中，[X,Y]和[εx,εy]分别是载体坐标系下的位置和误差。因此在水平直线航行的条件下，根据航向信息，通过式(3)可转化成载体坐标系下的坐标，通过选取一段时间的观测值，对拖体的垂直运动方向上的位置进行平滑，可明显提高其定位精度。上述方法更可作为无DVL观测信息时的重要补充。

2 自适应抗差无迹卡尔曼滤波

由于声信号在海水中的不稳定性，USBL和DVL观测值中往往存在大量的粗差观测。本节使用自适应抗差无迹卡尔曼滤波（Adaptive Robust Unscented Kalman Filtering,ARUKF）对USBL、DVL和深度信息进行融合。采用抗差IGG-3方案对粗差观测进行判定和处理，保证滤波算法在长时间观测下的稳定性。

2.1 状态方程和量测方程定义

定义状态模型参数：

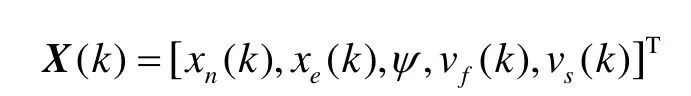
其中，xn(k)、xe(k)、ψ分别为北、东方向的位置和航向角，vf(k)和vs(k)为载体坐标系下的速度。非机动情况下的状态方程可简化为[7]：

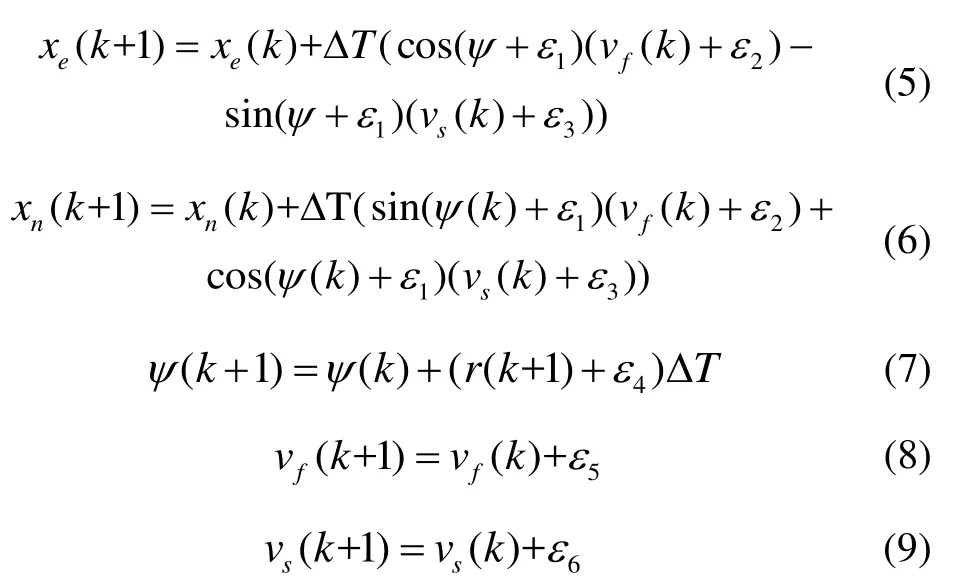
其中，ε表示过程噪声，ΔT为采样间隔。观测向量定义为且

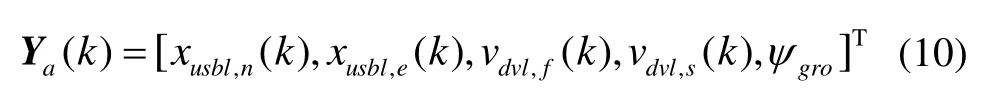
Ya(k)由 USBL在导航坐标系下的位置测量值(xusbl,n(k),xusbl,e(k))、DVL在载体坐标系下的速度测量值(vdvl,f(k),vdvl,s(k))以及航向角ψgro组成。深度约束信息可写为：

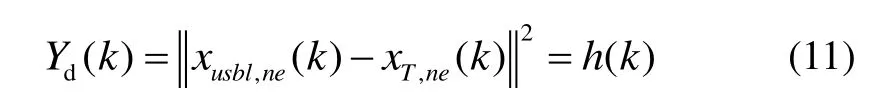
2.2 自适应抗差无迹卡尔曼滤波（ARUKF）

无迹卡尔曼滤波通过无迹变换（Unscented Transform,UT）给出的确定性采样，得到非线性变换后变量的均值和方差信息，理论上可以达到二阶以上的扩展卡尔曼滤波（EKF）精度。假设非线性方程为y=g(x)，如果已知变量x的均值和协方差矩阵Px，无迹变换过程如下[8-12]：

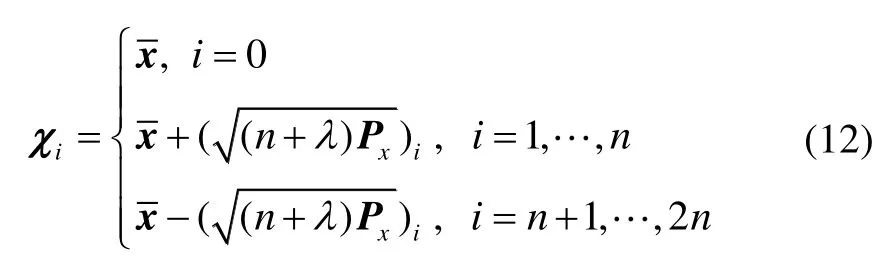
其中，χi表示采样点，n最小必要采样数，而λ可影响采样点到x的距离。点γi=g(χi)(i= 1,,2n)被依次计算，要估计的g(x)的均值及协方差矩阵Py和相应的权值及可快速求出。

自适应无迹卡尔曼滤波主要分为以下四个步骤：

1）初始化（计算初始状态及其协方差阵）

2）生成采样点

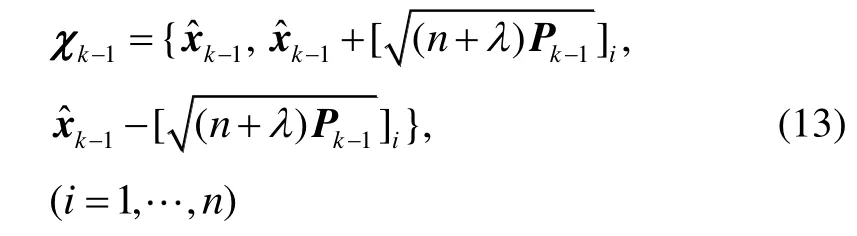
3）时间更新

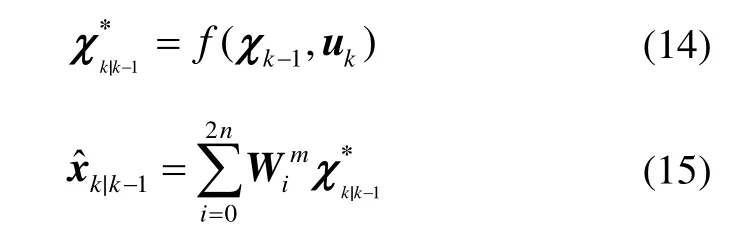
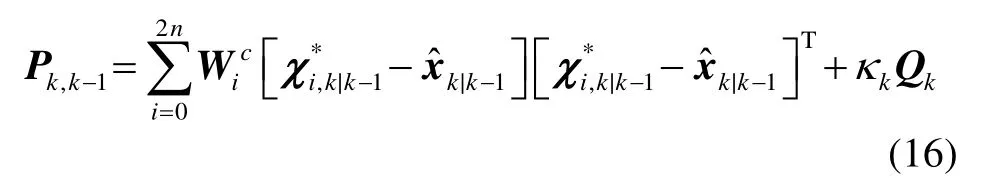
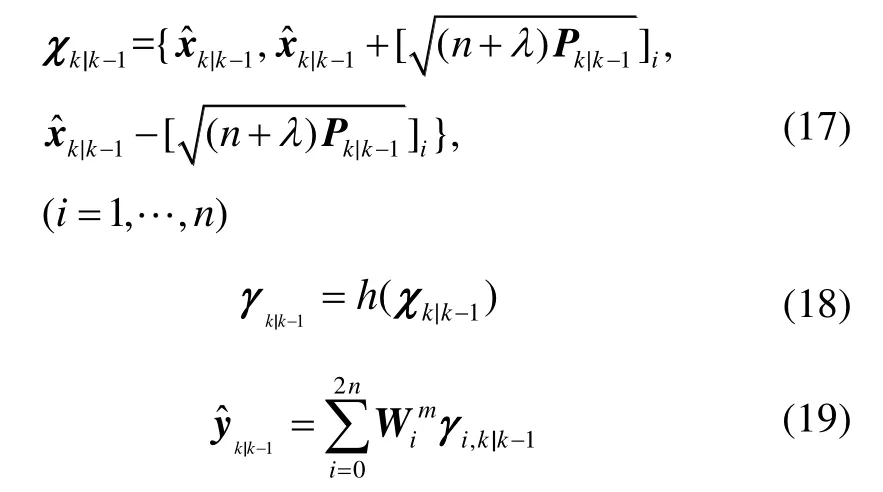
4）量测更新

本文主要通过新息序列和等价权函数来消除粗差观测值带来的影响。通过粗差对新息序列的异常影响对粗差进行识别，并通过量测矩阵的膨胀因子处理粗差观测值。具体过程如下：

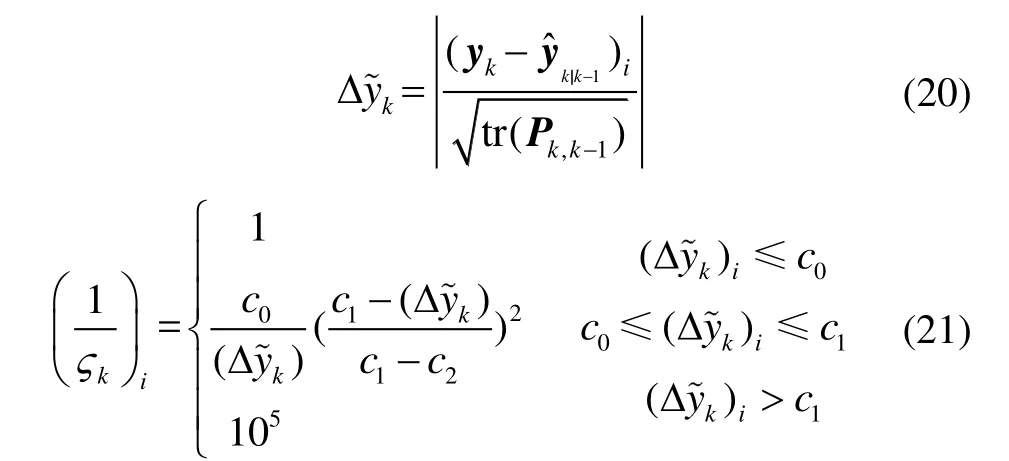
根据式(28)，膨胀因子ςk被分为正常、可能正常、异常三种情况，其中c0和c1可根据正常稳定的观测情况下的标准化残差数量级给出。修正后的观测值的协方差矩阵为：

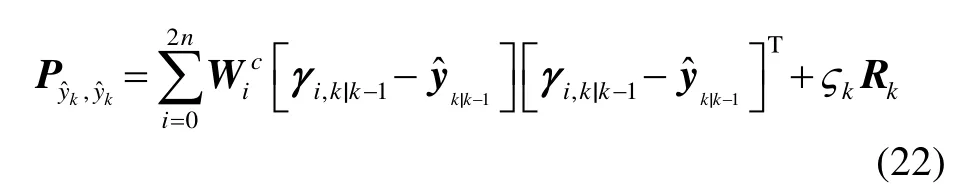
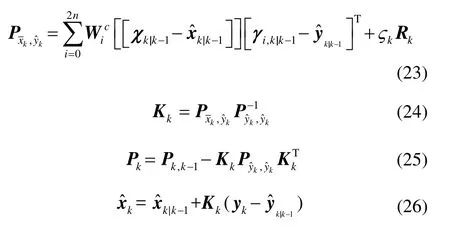
在深海中，非线性情况并不突出，但拖体上浮过程中，垂直约束方程的非线性程度会变强。而 UKF算法并不需要直接解算雅克比矩阵，能方便得到非线性方程的统计信息，在非线性较强的系统中明显优于一阶EKF滤波算法。当观测值中存在粗差观测值时，信息向量一般会出现异常，此时通过增大观测噪声矩阵使得滤波器拒绝该观测信息，仅从状态方程和其他观测信息预测出该时刻的状态信息，从而提高滤波器的容错性。

3 实验分析

3.1 仿真实验

首先通过仿真实验对基于深度约束的 ARUKF算法的定位精度和稳健性进行分析。仿真水深为5000 m，拖体以3 m/s 的常速度航行。导航传感器测量误差见表1。

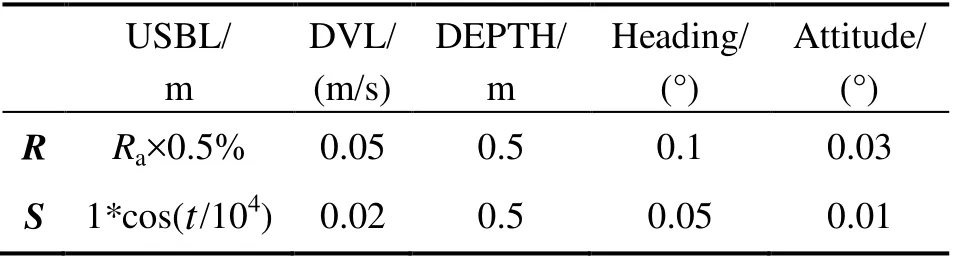
表1 USBL/DVL/Depth/Attitude仿真参数Tab.1 Simulation parameters of USBL/DVL/Depth/attitude

表1中，R表示随机噪声，S表示系统偏差。USBL基阵到信标的斜距为Ra，其测量精度为Ra/5000。DVL测量拖体在载体坐标系下的速度。母船和拖曳系统按图5的整齐的巡回模型航行。

使用30000个历元的直线观测值对平滑算法的性能进行测试，给出原始USBL结果、深度约束（USBL&DEPTH）的结果和MEDFILT平滑方案。MEDFILT方案是采用10个历元数据的开窗平滑算法（MEDFILT

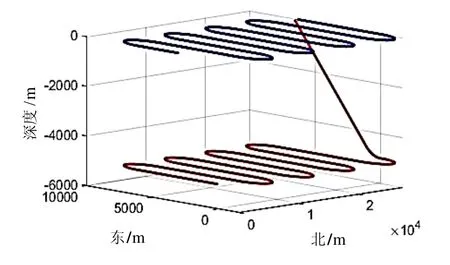
图4 水下拖曳系统的轨迹示意图Fig.4 Trajectory of underwater towed system

在本文指中值滤波方法）。MEDFILT方案首先将载体深度约束后的位置转换成载体运动坐标系，并在垂直于运动方向上进行平滑处理。

如图5所示，经深度约束（USBL & DEPTH）后的水平位置精度明显优于USBL原始观测值。为研究深度约束与拖体和母船运动状态之间的关系，绘制了缩小10倍的二者航向角之差YAW。垂直约束后精度变化的趋势同 YAW 的趋势明显相关，当存在较大定位误差的情况时，拖体水平位置杂乱无序，但经过深度约束改正后沿船航行方向上的定位精度明显提高，与上文分析的结论相符。因考虑到载体水平运动状态模型，MEDFILT 方案精度较 USBL&DEPTH 算法进一步提高。仿真实验采用平均绝对误差（ Mean Absolute Error,MAE） 来评定算法的平均精度，其定义为：

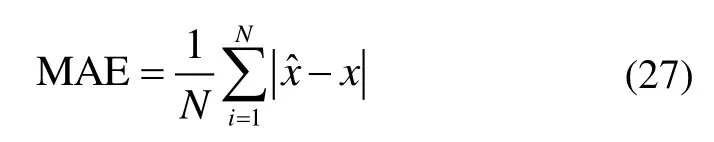
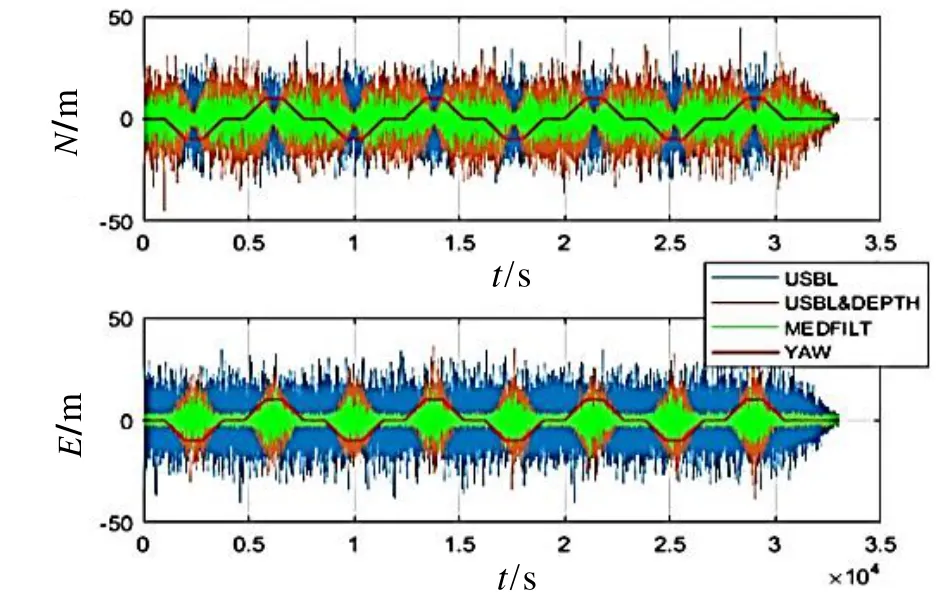
图5 开窗平滑算法定位误差图Fig.5 Positioning residuals of MEDFILT

表2给出前1000个历元的直线运动状态的解算结果。仿真实验中船沿北方向上航行，深度约束算法在北方向上的深度约束效果明显优于东方向。结合图5和表2 可得，MEDFILT 算法通过深度约束信息和开窗平滑处理，明显提高了直线状态下垂直于运动方向上的定位精度，当载体运动方向垂直的速度为 0时，MEDFILT方案在东方向精度较深度约束方法提高了4 m左右。

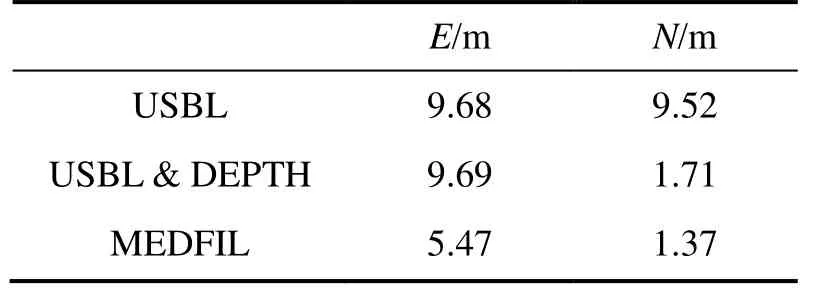
表2 直线状态下的平均绝对误差Tab.2 Mean absolute errors of straight line

为验证自适应无迹抗差卡尔曼滤波算法的精度和容错性能，本文分别设置了不含粗差和含粗差的两种实验，并采用标准无约束卡尔曼滤波（KF）算法作为对照。如图6所示，不含粗差情况下，ARUKF的定位精度最高，其精度明显优于KF滤波算法，证明了深度约束对滤波算法的提高。

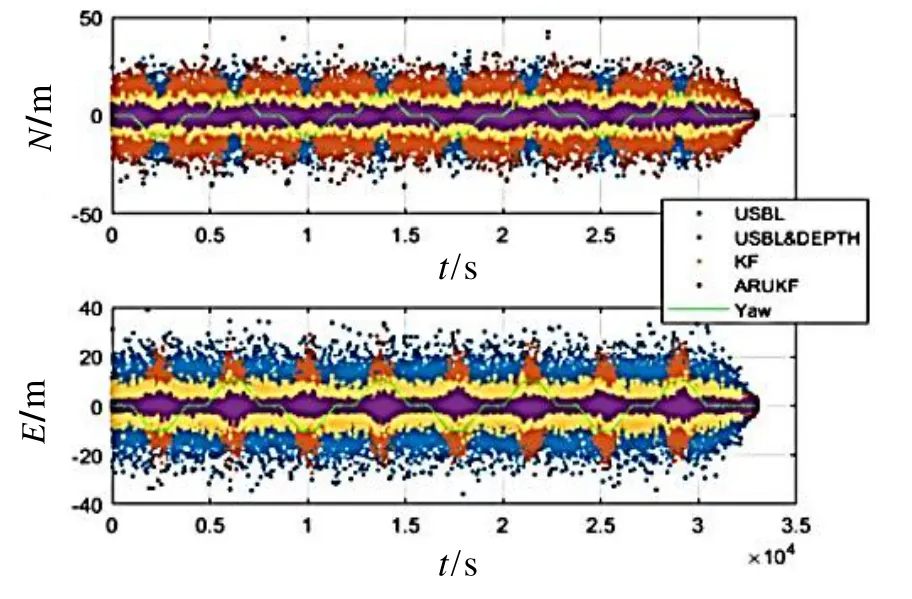
图6 不含粗差情况下的定位误差图Fig.6 Positioning residuals of four approaches without outliers

由表3可知，不含粗差的情况下，融合多普勒观测的KF和ARUKF滤波都可以提高载体水平定位的精度。由于垂直约束的影响，ARUKF算法在北方向上精度较KF滤波算法提高了接近2 m。

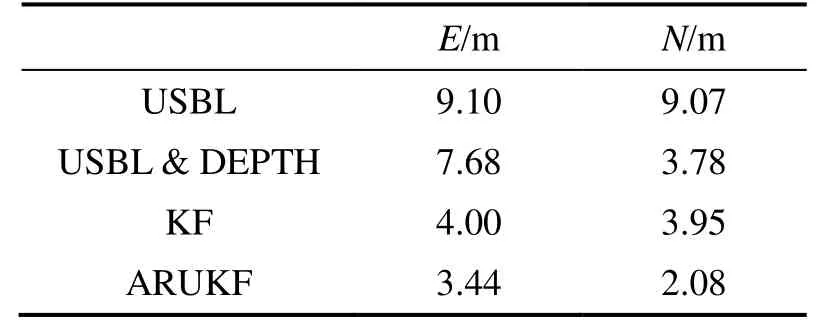
表3 不含粗差情况下的所有历元的平均绝对误差Tab.3 Comparison on Mean Absolute Errors of the epoch without outliers

含粗差情况时，在每100个USBL观测值中和每150个DVL观测中添加一个随机的粗差（10倍观测噪声），通过标准无约束卡尔曼滤波（KF）和有深度约束的无迹卡尔曼滤波（UKF）作为对照来验证算法的有效性。

如图7所示，当USBL和DVL数据中同时含有粗差时，此时的定位精度较其他时刻要差。ARUKF滤波效果要明显优于UKF和KF算法，证明了新算法的稳健性。

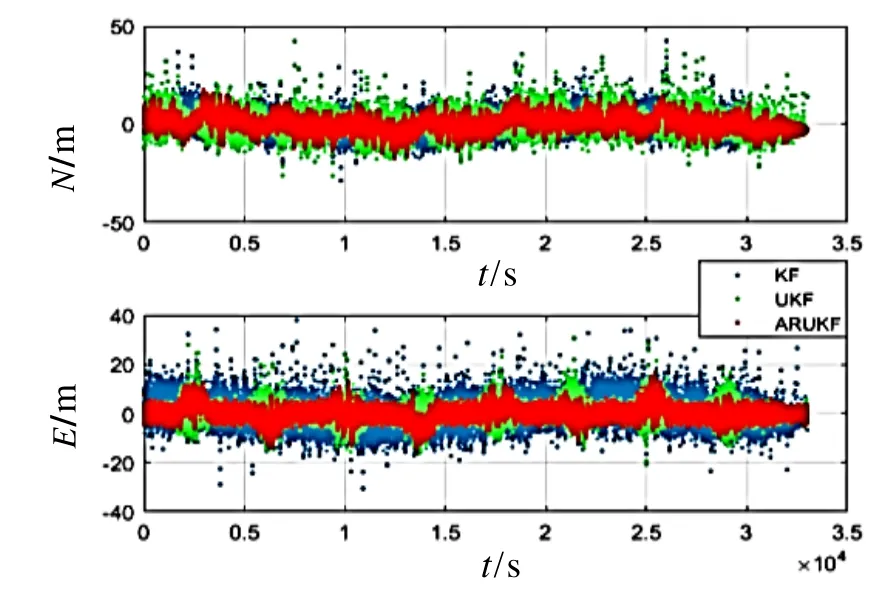
图7 含粗差情况下的定位误差图Fig.7 Position residuals of the three approaches with outliers

3.2 实测实验

图8(a)是采集的4500 m深的USBL数据，红绿蓝三种颜色的点分别表示早、中、后三阶段的位置。由图可见，USBL观测值的观测精度和采样率都比较低，并且含有一些粗差值。声学斜距信息如图8(b) 所示，其测距精度要明显优于其定位精度，这是本文深度约束的基础。

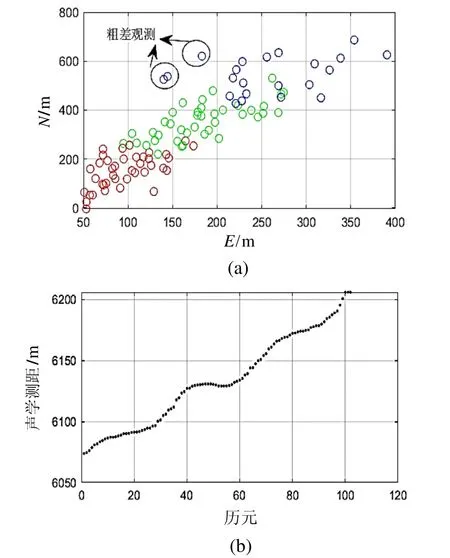
图8 实测USBL水平位置和斜距观测值Fig.8 Position and slant range of underwater towed vehicle by USBL

DVL传感器测得的速度信息如图9所示，由载体坐标系下的速度观测值的可看出，X方向上的速度值在0值附近波动且变化幅度较小，说明拖体沿直线运动且左右摆动较小。较USBL观测值，DVL和姿态传感器的观测值具有高精度和高采样率的特点。本文采用拉格朗日插值保证采用时刻的一致。

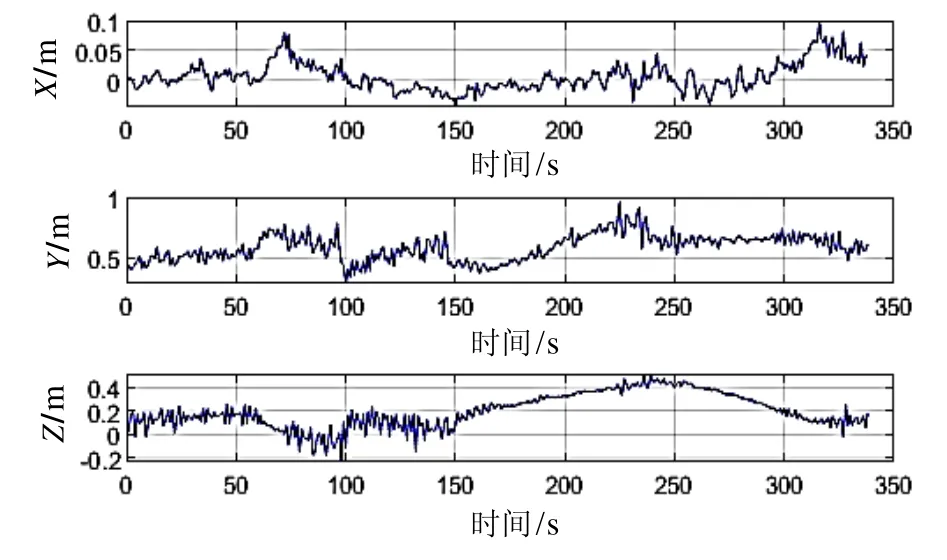
图9 水下拖体的多普勒速度信息Fig.9 Velocity of towed vehicle measured by DVL

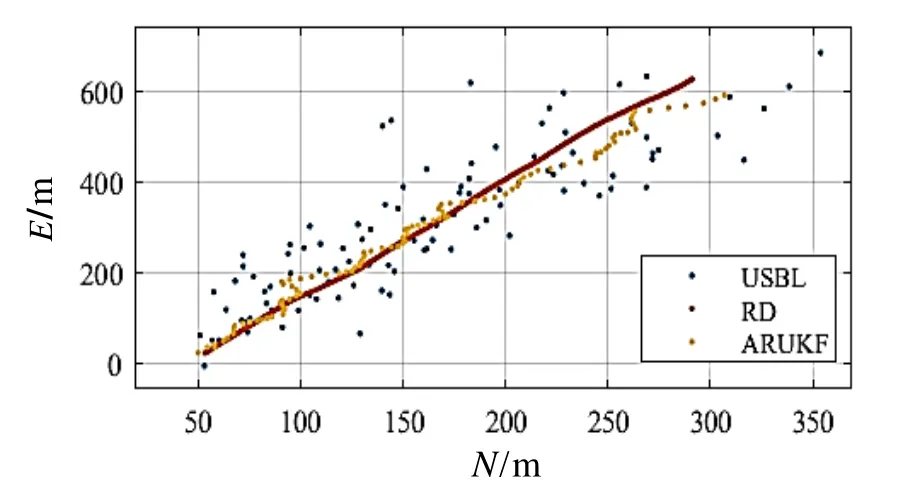
图10 基于ARUKF算法的水下拖体平面位置Fig.10 Position of towed vehicle by ARUKF method

由于USBL精度较差，且粗差较多，KF算法不适合作为对照，而深度约束后的点在垂直于前进方向上的离散程度依然很大，本文使用 DVL数据进行航迹推算（DR）作为对照。如图10所示，DR方法较USBL的位置更加平滑，因精度和采样率不够的问题，其在后期发散。使用深度约束的ARUKF算法定位精度在保证比较平滑的情况下，精度要高于DR算法，同时具有一定的抗差性能。

4 结 论

本文结合实测的深海拖体导航数据分析了导航传感器的性能，采用仿真数据和实测数据验证了新滤波算法的有效性。实验结果表明：基于深度约束的开窗平滑算法能有效利用USBL声学测距信息及深度约束信息提高水下拖体的定位精度；自适应无迹抗差卡尔曼滤波可以有效识别USBL数据和DVL数据存在粗差，提高算法的容错性；该算法能有效利用深度约束信息和拖曳系统直线状态模型，提高动态定位的精度。