浅论幼专生数学语言应用能力的培养

刘莉莉

【摘要】思维是语言的内核，语言是思维的外壳，思维的发展同语言的发展是紧密相关的.数学语言是一种特殊的语言，是数学思维的工具，是表达数学思想的最佳载体.数学语言不仅为数学本身，也为其他学科的数学应用提供了简洁的表达方式.我们应当把培养学生的数学语言和数学知识紧密结合起来，将它看成数学学习的重要组成部分.本文阐述了数学语言的特点、作用和幼专生数学语言应用能力培养的重要性，提出了从学生口头表达能力、书面语言运用能力和灵活运用多种数学语言这三个方面来综合培养学生的数学语言应用能力.

【关键词】幼专生;数学语言;应用能力

数学语言是人们进行数学表达和数学交流的工具，主要用来描述事物的数量关系、空间形式、结构以及逻辑关系.数学语言的运用能力反映了人理性思维的状态.联合国教科文组织将有效的数学交流作为学习数学的目标之一，而实现有效交流的前提是学习和掌握数学语言.

作为一名大學生，不仅要重视数学知识、数学方法、数学思想的学习，也应该重视数学语言的学习和训练.从笔者多年来的授课情况看，传统的教学对学生数学语言能力的培养不够，更多的是关注学生的写.学生对数学语言的特点理解不深，数学语言的运用能力较差，想说但说不明白，或者是不敢说、不愿说.

一、数学语言的特点

数学语言具有明晰、严谨、简洁、规范的特点，它的魅力令人惊叹.数学具有高度的科学性，每一个概念都有明确、清晰的含义，概念一经界定，这个定义就要随着这个词贯串始终，不能再有任何改变.定理的推导过程和叙述是严谨的.语言的表达是精确有条理的.学了多年的数学，我们会发现，许多复杂的客观现象的规律，往往可用十分简单的公式语言来呈现.比如，人们捕鱼的渔网具有这样的几何规律：无论用什么质量的绳索织渔网，无论所织的网有多大，它的结点数（V）、网眼数（F）和边数（E）都可用公式V+F-E=1来表示，这种规律在三维中的情形，就是多面体的欧拉公式 V-E+F=2.这个简单的公式，概括了世界上成千上万个多面体的共同特性.可见，数学语言是最简洁的文字，却能反映出深刻的客观规律，正如爱因斯坦所说：“美在本质上终究是简单性.”

二、数学语言的作用

数学是一门严谨的科学，以语言为载体展现数学的理性思维.一百多年前，只有力学、天文学和某些物理学的分支使用数学完善其理论，化学很少用到数学，生物学与数学毫无关系.而现在的社会科学、自然科学和人文科学各个领域都在大量地应用数学理论.这正是进入21世纪人类社会和自然面貌迅速改变的原因.随着数学越来越多地渗透到各个领域，想要精确地表述某种现象、规律、问题，不可避免地要使用数学语言.因此，有人说“世界这本大书，是用数学语言写成的”“要是没有数学语言，宇宙几乎是不可描述的”.数学语言的作用由此可见一斑.

三、幼专生数学语言应用能力培养的重要性

（一）有利于学生自身的发展

培养数学语言应用能力不仅有利于学生更好地理解和掌握知识，提高学生的数学语言表达能力，而且有利于促进学生思维能力的发展，久而久之，学生渐渐地开口说、大胆说，就会越学越有自信.

（二）有利于学生胜任今后的数学教学工作

大部分学生毕业后将从事幼儿教师的职业，开展幼儿数学的启蒙教育.在幼儿教学阶段，幼儿处于前运算阶段，它的早期是语言的快速发展期，这一时期的儿童逐渐学会用语言表达概念知识.因此，教师自身的语言应用能力至关重要.这就要求教师本身要明了数学语言的特点，能规范使用数学语言来表述各种数学概念，同时能够引导幼儿在操作中、游戏中准确地理解各种符号功能.

四、如何培养学生数学语言的应用能力

（一）培养学生的口头表达能力

1.鼓励学生自主学习，善于使用数学语言总结概括.

比较简单易懂的内容，教师可以布置阅读提纲，对于一些理论性不是很强的内容，学生自己先阅读，勾画重点，然后要求他们使用简洁、规范的语言严谨、清晰地概括内容.如幼专教材中的“数学发展简史”，可以按照每个阶段的时间节点、代表人物和取得的主要数学成果这个线索进行学习;又如，“历史上的三次数学危机”，学生可以通过自学，厘清事件的经过，并能简要说出每一次危机产生的原因、危机的实质及如何解决的.又如，“有无限个房间的旅馆问题”是数学中构造出来的问题，为了让学生感受“有限”与“无限”的区别，体会无穷的魅力.有无限个房间的旅馆客满后仍然可以安排住宿，客满指有无穷个客人住进了无穷个房间，每一个房间都有人住，并且每个房间只住一人.它主要讨论了三类问题：第一类问题是客满后又来了有限个人，假设是M个人，该怎么安排住宿？方法就是先住进去的人依次往后挪M个房间，1号房的人搬到（M+1）号房.第二类问题是客满后又来有限个旅行团，假设为N个团，每个团都有无限个人，方法是把先来的无限个人看作一个团，与后来的团一起分房间，把房间（N+1）个一份、（N+1）个一份……地分.第三类问题是客满后又来了无穷个团，每个团都有无限个人，方法是给每个团的每个人进行编号分房间.这些规律教师可以在讲解中引导学生自己总结，只有学生真正理解了这些问题，才能够用简洁的语言总结出其中的规律.

2.分组讨论，畅所欲言.

教师可以在课堂上设计一些有趣的思考题让学生回答，并要求学生以小组合作的形式完成任务.首先，在小组内讨论，每名学生都参与讨论，各抒己见，然后每个小组选派代表发言（要求每个小组每次选派不同的代表发言），这样既能提高学生学习的积极性，也能让每一名学生有表达的机会.比如，幼专教学中“悖论与无限”一节中，教师通过下面的思考题引入：①如果说神是万能的，他能否创造一块他举不起来的大石头？②有一天，一个大灰狼抓住了一只小白兔，并对小白兔说：“你说我会不会吃掉你，如果说对了，我就放了你;如果说错了，我就吃掉你.”问：“小白兔能否脱离险境？怎么回答才能脱离险境？”学生对这类问题比较感兴趣，教师由浅入深创设情境，引导学生充分讨论，以组为单位得出结论，小组代表发言回答，从而教师引入悖论的概念，接着要求学生以组为单位举出悖论的例子，学生先在组内讨论，每组回答时不能有重复的答案.最后大家讨论列举的例子是不是悖论，并说明原因.学生不仅逐步加深了对概念的理解，而且在讨论中也不断地提升了数学语言的应用能力.

3.分层设计，鼓励学生站起来表达.

教师在教学中可以适当地设计一些简单的问题，使基础较弱的学生也能够有机会表达.如这样一个问题：史密斯家里有一个老式的烤面包器，一次只能放两片面包，每片烤一面.要烤另一面，你得取出面包片，把它们翻个面，然后放回烤面包器中.烤面包器对放在它上面的每片面包正好要花1分钟的时间烤完一面.一天早晨，史密斯夫人要烤3片面包，两面都烤.她花了4分钟时间.史密斯先生看了他夫人的操作后，说：“亲爱的，你可以用少一点的时间烤完这3片面包.” 思考：怎样花更少的时间烤完这3片面包？这个问题很简单，学生都能够很快地思考出答案，因为简单，愿意回答的学生也比较多，但是大部分学生的表达不够准确、清晰，他们所用的语言基本都是这片面包、那片面包、最后一片面包、先烤一面、再烤另一面等等，其实我们给面包命个名就可以了：把3片面包叫作A，B，C，每片面包的两面分别用数字1，2代表. 第一分钟：烤A1面和B1面. 一分钟后，取出面包片，把B翻个面放回烤面包器.把A放在一旁而把C放入烤面包器.第二分钟：烤B2面和C1面.烤好后，取出面包片，把C翻个面放回烤面包器.把B放在一旁而把A放回烤面包器.第三分钟：烤A2面和C2面.三分钟后，3片面包的每一面就都烤好了.这样叙述既简单又明了，学生容易理解，在以后遇到类似的问题时都能够很好地解决.

（二）提高数学书面表达能力

1.规范书写.

不论是课堂上的练习还是课下作业，要求学生规范地使用各种数学语言，因果关系、先后逻辑等要厘清.教师要及时引导学生辨别陈述中的错误，并找出原因，避免错误再次发生.同时教师在作业批改中要注明问题，针对作业中的突出或是有代表性的表达错误，教师在课堂上要纠正，也可在课堂上展示优秀作业.比如，这样一道思考题：老师让6名学生围坐成一圈，让另一名学生坐在中央，并拿出七顶帽子，其中四顶白色、三顶黑色，然后让7名学生都戴上眼罩，并给每名学生戴一顶帽子;再只解开坐在圈上的6名学生的眼罩，这时，由于坐在中央的学生的阻挡，每个人只能看到五个人的帽子.老师说：“现在，你们七人猜一猜自己戴的帽子的颜色.”大家静静地思索了好大一会儿.最后，坐在中央的被蒙住双眼的学生说：“我猜到了.”教师问：中央的被蒙住双眼的学生戴的是什么颜色的帽子？他是怎样猜到的？学生在回答这个问题时，要么烦琐冗长，要么不能切中要点，只有极个别学生能够准确、清晰、言简意赅地表述出来.我们可以这样解答：坐在周围的学生只能看到5顶帽子，可能的情况有：（1）看到4白1黑;（2）看到3白2黑;（3）看到2白3黑.对于（1）和（3），他们能很快地猜出自己戴的帽子的颜色，但是，“大家靜静地思索了好大一会儿”，猜不出来，说明他们只能看到3顶白帽2顶黑帽，也就是说坐在周围的每名学生和他对面的学生戴的帽子是1顶黑帽1顶白帽，总共有3顶黑帽3顶白帽，剩下1顶白帽，所以坐在中间的学生戴的是白色的帽子.

2.撰写数学小论文.

作为一名学前教育专业的学生，将来绝大部分会从事幼儿教育，写论文是不可避免的.因此，在我们的教学中有一项综合素质的考查，即要求学生在一学期的时间内课外阅读一到两本与数学有关的书籍，然后根据阅读内容，自拟题目，撰写一篇格式标准、规范的数学小论文，使学生通过论文的小练笔训练数学语言的运用能力，当然，也可以教师拟好题目，学生自己选择题目撰写论文.尝试下来，有极个别学生能够交出质量稍高的小论文，他们能通过多种途径进行调查和收集资料，运用较规范的数学语言阐述问题.

（三）灵活运用多种数学语言

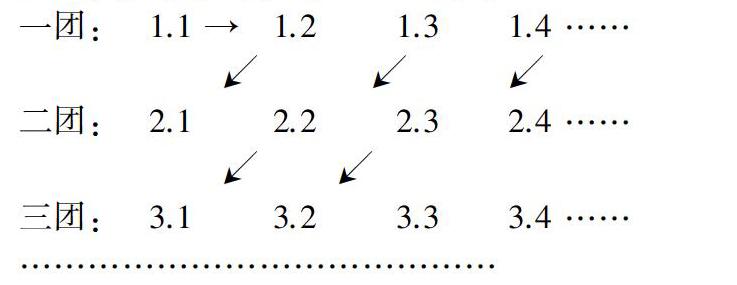
数学语言虽然要以自然语言作为载体，但它是形式化的语言，在形式化方面，不随民族、地域的不同而不同.数学语言是一种由数学符号、数学术语和经过改造的自然语言构成的科学语言.数学语言是文字语言、符号语言、图形语言的交融，数学思维用符号表达简洁、精练，用文字表达生动，用图形表达直观、形象，但是有些问题用文字表达太繁杂，用符号表达又太抽象，用图形表达有时又不全面.因此，我们必须对数学语言的多种形式进行灵活的转换.教师要善于引导学生使用多种语言来表达.比如，有无限个房间的旅馆问题中，客满后又来了无穷个旅游团，每个旅游团中都有无穷个客人，老板该怎么安排？我们可以先用下面的图形语言来表示，给出规律，再配以文字解释.

老板可以让原来房间里的客人都出来，这无穷个客人看作一个团，将所有旅游团的客人统一编号排成上图，按箭头依次进入1，2，3，4，5，…各号房间入住，则所有人都有房间住.这样图文并茂，更易理解.

当然，学生从学习数学语言到掌握数学语言的过程不是一蹴而就的，需要长期地训练.只有理解了数学语言的来龙去脉及意义，并且能熟练地掌握它们的各种用法，对它们有了理性的认识之后，在数学学习中才能灵活地对它们进行各种等价叙述，达到数学语言学习的最高水平.

【参考文献】

[1]顾沛.数学文化[M].高等教育出版社，2008.6.

[2]齐斯·德福林.数学的语言[M].广西师范大学出版社，2013.1.

[3]侯旭鹏. 浅谈数学教学语言的锤炼[J]. 大学时代，2006（7）：77.