利用不动点求解定义新运算

广东省华南师范大学(510631) 李文丽 韩彦昌

一、概念判定

定义新运算是指用一个符号和已知运算表达式表示一种新的运算[1].定义新运算是经过特别设计的一种运算,它使用的是一些特殊的运算符号,如：∗,Δ等,通常需要转化为常规的四则运算算式进行计算.

对于给定函数y=f(x),满足方程f(x)=x的解,称为函数y=f(x)的不动点[2].

不动点法在初等教育中主要应用于递归数列和迭代函数之中,本文尝试应用不动点法解决定义新运算问题.

二、定义两种新运算

定理1规定运算“∗”,使得对任意复数a,b,有a∗b=(p,q,a+b̸=q为实常数),记x0,x1为g(x)=的不动点,则有以下两个结论：

(1)当q2+4p̸=0,即x0̸=x1时,构造函数f(x)=,有f(a∗b)=f(a)f(b).

(2)当q2+4p=0,即x0=x1时,构造函数f(x)=,有f(a∗b)=f(a)+f(b).

证明：令g(x)=x,则g(x)==x,有x2+qx-p=0.

(1) 当q2+4p̸=0时,构造函数f(x)=x0,x1是不动点,所以有所以有

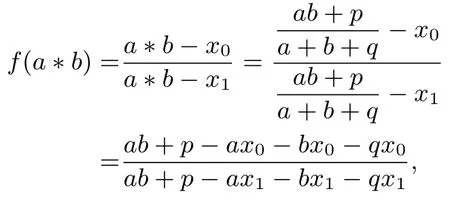
且

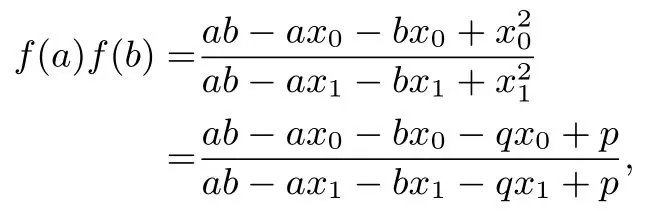
因此有f(a∗b)=f(a)f(b).

(2)当q2+4p=0时,x2+qx-p=0有唯一的解构造函数故

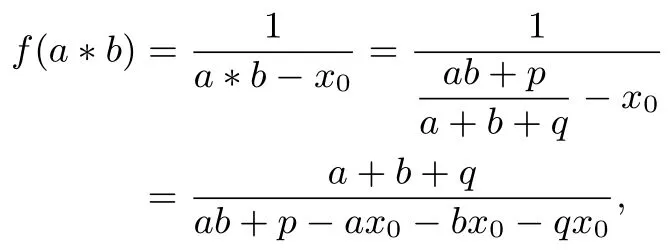
而

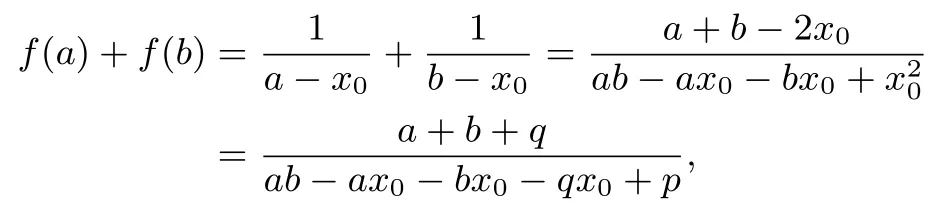
因此有f(a∗b)=f(a)+f(b).

注记1定理1中的∗是满足交换律和结合律的,即对任意复数,有a∗b=b∗a,以及

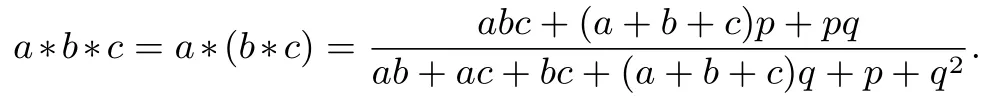
注记2易证对于不同的复数a1,a2,···,an,在定理1的条件(1)下,有

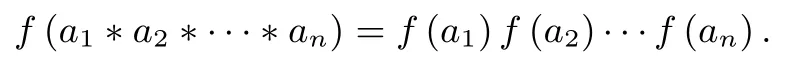
在定理1的条件(2)下有

例 1规定运算“∗”,使得对任意复数a,b,有a∗b=,a̸=-b,如1∗3=,求P=(1+i)∗(1+2i)∗···∗(1+9i)∗(1+10i)的值.

解析设g(x)=,令g(x)=x,得x2+1=0,解得不动点为x0=i,x1=-i,构造函数f(x)=由定理1有

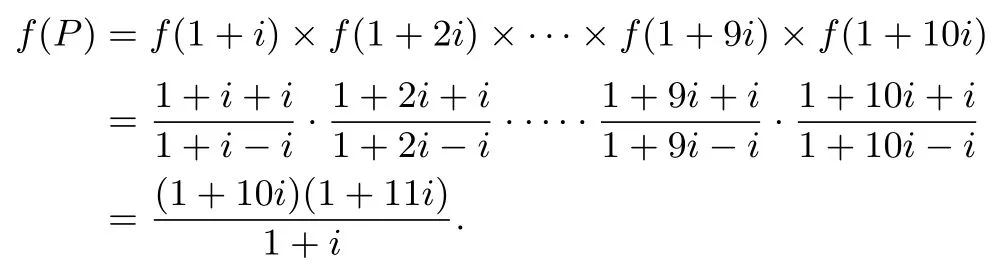
例2规定运算“∗”,使得对任意复数a,b,有a∗b=求A=-99∗(-98)∗···∗98∗99 的值.

解析设令g(x)=x,得x2+4x+4=0,解得唯一的不动点为x=-2,构造函数类比例1的分析,可得

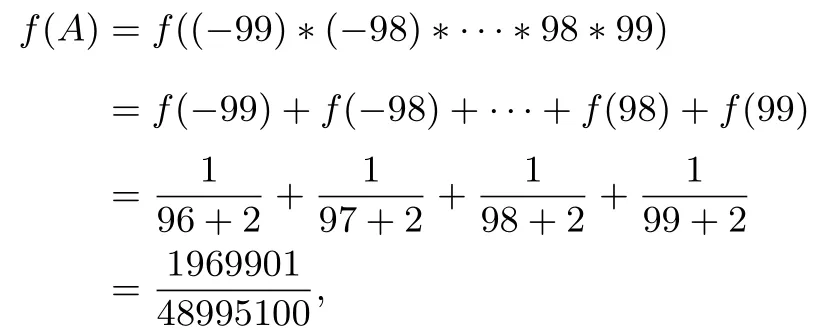
注记3(1)上述两例表明直接计算“∗”运算比较麻烦,可以构造适当的函数f(x),先求f(A)的值,再反演回去,求出A的值.定理中函数f(x)的作用在于将先进行“∗”运算,再进行函数运算变为先进行函数运算再进行乘法(或加法)的四则运算.

(2)当函数的不动点是两个相异的实数时,同定理1(1)的结论一样,也可以根据此来设计题目.

(3)可以改变定理中的分子与分母的位置,此时的求解就用到了倒不动点,如定义x∗y=求(···((2018∗2017)∗2016)∗2)∗1的值.求解过程中,令,求出倒不动点x=±2,有x∗2=可求得答案.

定理 2规定运算“∗”,使得对任意实数a,b,有a∗b=a+b+qab(q∈R且q̸=0),记x1为g(x)=qx2+2x的不为零的不动点,即则构造函数f(x)=x-x1,有f(a∗b)=q·f(a)f(b).

证明令g(x)=x,得qx2+x=0,得不动点为x0=0,x1=,则有

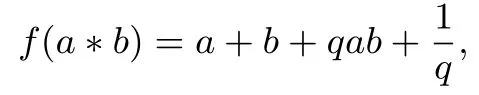
且

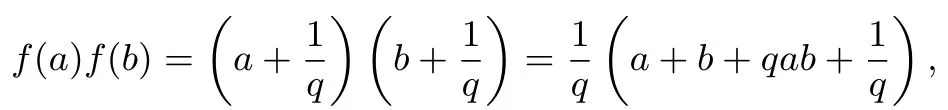
因此f(a∗b)=qf(a)f(b).

注记4同定理1中注记1和2,定理2中的“∗”运算满足交换律和结合律,且

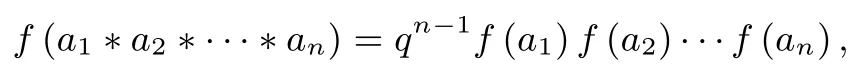
其中a1,a2,···,an为任意实数.事实上,

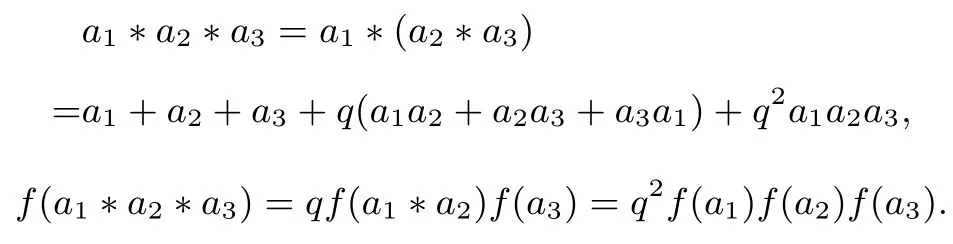
例3规定运算“∗”,设a∗b=令,求Q=sinθ∗sin2θ∗···∗sin8θ的值.

解析依题意得(a∗b)2=a2+b2-2a2b2,令c=(a∗b)2,a1=a2,b1=b2,则有c=a1+b1-2a1b1,令g(x)=2x-2x2,由定理2可得其非零不动点为x=,可构造函数有f(a∗b)=-2f(a)f(b),且θ=则可得

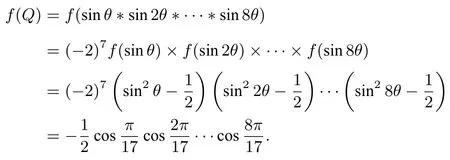
令

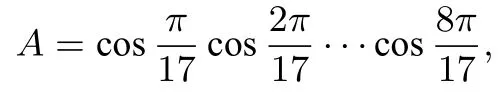
令

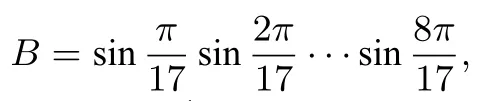
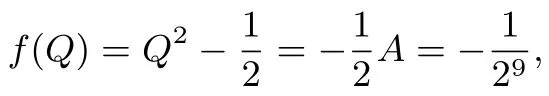
三、结语

定义新运算作为数学竞赛的重要考点,解决或命制定义新运算题一般没有固定的方法,本文提供一种解决或命制定义新运算试题的新思路.