分离函数法在函数问题中的应用

广东省深圳市高级中学(518040) 高军

数学教学离不开解题,解题的关键是掌握基本的技巧和方法.在解题教学中,教师要引领学生主动探究,勇于创新,积极发现有效的解题技巧与方法,创造性的解决问题.本文主要通过一道函数题的解法探究与变式探究,多视角介绍分离函数法在函数问题中的应用.所谓分离函数法,是指我们在解题过程中结合问题实际,将同一关系F(x,a)中的两类不同函数分离开来,让研究的问题变得直观,让研究的过程变得简单,达到化繁为简、化陌生为熟悉的目的.

一、问题及解法探究

题目函数f(x)=lnx-ax2+x有两个零点,则实数a的取值范围是

A.(0,1) B.(-∞,1) C.D.

解法探究两种思路与四种解法.思路一,将f(x)的零点个数转化为函数图象与x轴的交点个数,直接研究f(x)图象即可.思路二,进行函数的分离,将f(x)的零点个数转化为两函数图象交点个数.

解法1(整体函数法)函数定义域为(0,+∞),f′(x)=,若a≤0,因为x＞0,所以f′(x)＞0,故f(x)在(0,+∞)单调递增,不合题意;若a＞0,则存在x0＞0,使得f′(x0)=0,当x∈(0,x0)时,f′(x)＞0,当x∈(x0,+∞)时,f′(x)＜0,故f(x)在(0,x0)单调递增,在(x0,+∞)单调递减.又当x→0时,f(x)→-∞,当x→+∞时,f(x)→-∞,要使f(x)有两个零点,则满足f(x)的最大值f(x0)=lnx0-ax20+x0＞0,又故f(x0)=lnx0+x0-1＞0,易得：x0＞1.又0＜a=故0＜a＜1.

解法2(分离常数函数)由f(x)=0得：a=,设g(x)=,g′(x)=,由g′(x)＞0 得0＜x＜1,由g′(x)＜0得x＞1,故g(x)在(0,1)单调递增,在(1,+∞)单调递减,故g(x)的最大值为g(1)=1.当x→+∞时,g(x)→0,当x→0时,g(x)→-∞,结合两函数y=a及y=g(x)图象,如图1所示,要使f(x)有两个零点,故0＜a＜1.

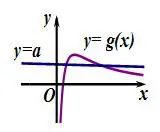
图1

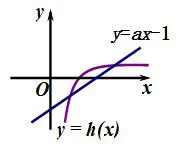
图2

解法3(分离一次函数)由f(x)=0得设,由h′(x)＞0得0＜x＜e,由h′(x)＜0得x＞e,故h(x)在 (0,e)单调递增,在(e,+∞)单调递减.当x→+∞时,h(x)→0,当x→0时,h(x)→-∞,又直线y=ax-1恒过定点(0,-1),设直线y=ax-1与曲线y=h(x)相切于点(x0,y0)(0＜x＜e),则,解得x0=1,y0=0.故当直线y=ax-1与曲线y=h(x)相切时,a=1,又x∈(0,e)时,y=h(x)的二阶导数恒大于0,故y=h(x)为向上凸函数,结合两函数图象,如图2所示,易得实数a的取值范围是a∈(0,1).

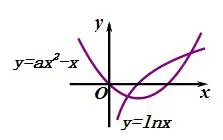
图3

解法4(分离对数函数与二次函数)由f(x)=0得lnx=ax2-x,由函数y=lnx与y=ax2-x图象可知,要使函数图象有两个交点,则a＞0,当两函数图象在点(x0,y0)有公切线时,则易解得：x0=1,y0=0,a=1.结合两函数凹凸性及图象,如图3所示,要使两函数图象有两个交点,则,即0＜a＜1.

由上述过程可知,解法1的解题过程较长,解题层级较多,需要分类讨论,且过程较为复杂.解法2、3、4体现了分离函数法在解决函数问题中的应用,解法的本质是将所要解决的问题转化为直线与曲线、曲线与曲线的位置关系问题,让问题变得直观清晰,解法变得简单明了.

二、变式探究

变式一(1)函数f(x)=alnx-x2+x有两个零点,则实数a的取值范围是____;

(2)函数f(x)=lnx-x2+ax有两个零点,则实数a的取值范围是____.

思路以上变式是题目中参数a的位置发生变化而产生的,其解决问题的方法与题目的解法探究一致,限于篇幅,解析过程从略,读者不妨试一试.答案：(1)(0,1)∪(1,+∞);(2)(1,+∞).

变式二设函数f(x)=lnx-x3+2ex2-ax,若函数f(x)至少存在一个零点,则实数a的取值范围是____.

思路函数f(x)由指数函数与三次函数组合而成,直接用导数工具研究f(x)的零点,过程较为复杂.换个思路,将其中的二次函数分离出来,化陌生为熟悉,把f(x)的零点个数转化为两个熟悉函数的交点个数,问题迎刃而解.

解析由题意得易得函数在(0,e)单调递增,在(e,+∞)单调递减.故g(x)在x=e取极大值函数h(x)=x2-2ex+a在x=e取极小值h(e)=-e2+a,结合两函数图象,可得h(e)≤g(e),故.

变式三已知函数f(x)=(x+1)lnx-a(x-1).若当x∈(1,+∞)时,f(x)＞0,求实数a的取值范围.

思路本题考查不等式恒成立问题,首先分离函数y=lnx,使lnx前的系数变为常数,不再含有x,然后构造函数对其求导,可使导函数简洁有效,达到求解目的.

解析当x∈(1,+∞)时,由f(x)＞0分离指数函数得：,则

(1)当a≤2时,x∈(1,+∞),x2+2(1-a)x+1≥x2-2x+1＞0,故g′(x)＞0,g(x)在x∈(1,+∞)上单调递增;因此g(x)＞0;

(2)当a＞2时,令g′(x)=0得：x1=a-1-由x2＞1及x1x2=1得x1＜1,故当x∈(1,x2),g′(x)＜0,g(x)在x∈(1,x2)单调递减,因此g(x)＜0.综上,a的取值范围是(-∞,2].

变式四已知方程xex=x+2在区间[k,k+1]上有解,求整数k的值.

思路本题实际上是探求函数零点所在的区间,这就要先探求零点的个数,因而必须先考虑函数的单调性.如果令函数f(x)=xex-x-2,则其单调性不易判断,问题解决困难,因此必须变形,如何变形呢?将指数函数ex分离出来,这一方法确实使问题变得十分简单,而其他方法则很难解决.

解析显然x=0不是原方程的解,则原方程等价于令所以f(x)在 (-∞,0)和 (0,+∞)上单调递增.因为f(1)=e-3＜0,f(2)=e2-2＞0,f(-3)=e-3-＜0,f(-2)=e-2＞0,所以方程xex=x+2有且只有两个实根,且分别在区间[1,2]和[-3,-2]上,所以k=1或k=-3.

变式五证明.

思路分离初等函数的组合函数.函数等式左边式子同时出现指数函数与对数函数,直接构造函数,转化为求函数最小值会显得比较困难,变换思路,经过变式将指数函数与对数函数分别位于不等式两边,化难为易.

解析原不等式等价于xlnx＞xe-x-,易得g(x)=xlnx在上单调递减,在上单调递增,从而g(x)在(0,+∞)上的最小值为易得在(0,1)上单调递增,在(1,+∞)上单调递减,从而h(x)在(0,+∞)上的最大值为;但两个函数取最值时的自变量不同,因此等号取不到,从而得证.

变式六已知x＞0,求证：(x+1)ex+x2+3x-4-2lnx＞0.

思路不等式左边的式子是指数函数、对数函数、一次函数、二次函数的四则混合运算,形式较为复杂,如果直接求导,证明左边函数的最小值大于0,过程会陷入困难的境地.变换思路,通过分离初等函数的组合函数,将问题转化为两个初等函数最值的大小比较,问题会变得简单,达到化繁为简的目的.

解析原不等式等价于(x+1)ex-4＞2lnx-x2-3x,设g(x)=(x+1)ex-4,易得g(x)在(0,+∞)单调递增,故g(x)＞g(0)=-3;设h(x)=2lnx-x2-3x,易得h(x)在单调递增,在单调递减.从而h(x)在(0,+∞)上的最大值为又显然28＞e5,故,原命题得证.

三、延伸思考

素养导向的高考命题重视学科观念、规律的考查,考查学生扎实的学科基础,引导学生去形成思维中的惯性观念,并且能够合理进行转化.分离函数法本质是将要解决问题进行了合理转化,应把握的原则：分离后的函数的图象便于研究,让要解决的问题变得简单、清晰.有些问题可综合应用多种分离函数的方法来求解,因直线的特殊性,故我们常常优先考虑分离参数,然后考虑分离一次函数,最后才是想到分离曲线函数.

素养导向的高考命题注重科学探究能力的考查,研究开发探究型、开放型试题,发挥各种题型的组合功能,拓展学生思维空间.注重一题多解,一题多法,拓宽学生的解题思路.当然并不是所有函数问题都可用分离函数法来解决,在具体的解题实践中,教师须引导学生灵活选用适当方法求解,不断提高学生解题能力,提升学生的数学核心素养.

四、应用探究

1.(2016年高考数学全国卷Ⅰ理科第21题改编)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点,则实数a的取值范围是____.(答案：(0,+∞).提示：分离常数函数或一次函数)

3.(2011年高考数学全国卷Ⅰ文科第21题改编)已知函数曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.当x＞0,且x̸=1时,求证(提示：分离对数函数)

4.(2018年广东五校联考理数第21题改编)设f(x)=(x-1)2ex,判断并证明是否存在区间[a,b](a＞1),使函数y=f(x)在[a,b]上的值域也是[a,b].(答案：不存在.提示：问题转化为方程有两个大于1的不等实根)