由一道“赛题”谈投影法求四边形面积的应用*

江西省萍乡中学(337000) 黄贤锋 王 娇

一、赛题呈现

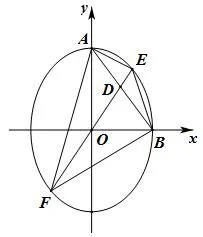
图1

赛题如图1,在平面直角坐标系中,椭圆方程为1,A,B分别为上顶点和右顶点,过原点O的直线与线段AB交于点D,与椭圆交于E,F两点,求四边形AEBF面积的最大值.

这是文[1]作者在一次“说题比赛”中的“赛题”,作者展示了该题的五种解法,视角多样,解法巧妙,笔者读后感觉受益匪浅,不忍释卷,于是把它作为我校的月考试题.阅卷发现该题的得分率很低.绝大部分同学是按照文[1]中的解法1的思路进行求解,但大多又半途而废.为了叙述的方便,现将解法1摘录于下：

解设点E,F到直线AB的距离分别为h1,h2,则SAEBF=S△AEB+S△AFB=即求h1+h2的最大值.EF的方程是y=kx,代入椭圆方程得所以

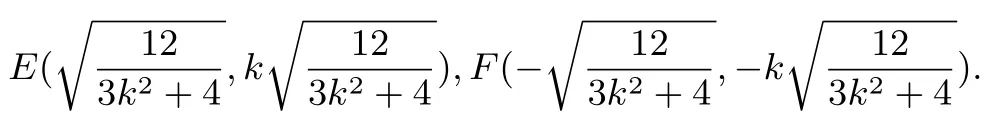
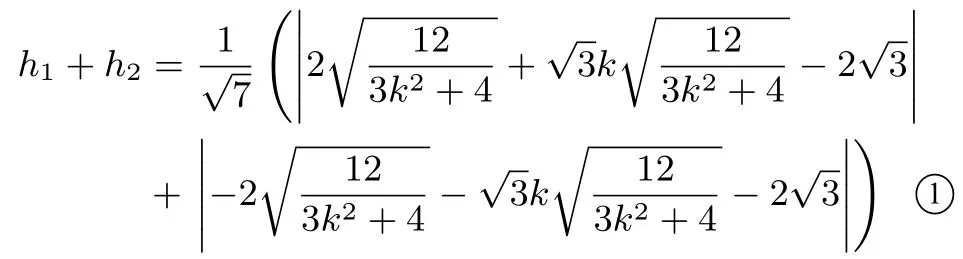
点E在直线AB的上方,点F在直线AB的下方,所以由线性规划知识：

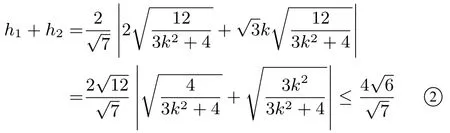
学生在解题过程中出现的问题主要有以下两个方面：(1)不会借助线性规划知识化简①式,使得解题半途而废.(2)对于②式,能力要求较高,涉及到系数的配凑,基本不等式的灵活运用,使得最终无法求出最值.

二、赛题另解

经过认真的思考,笔者发现可以将h1+h2视为一个整体,通过计算在AB的方向向量上的正投影得到h1+h2的表达式,最终解决本题,解法如下：

解由已知易得记AB的法向量设则,所以

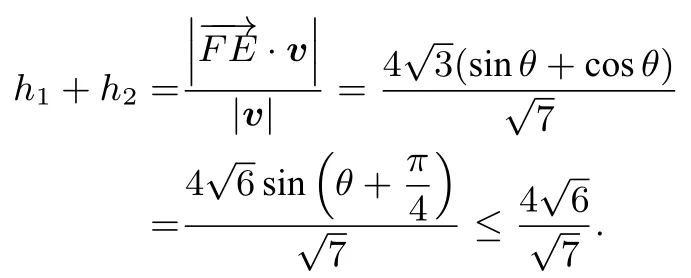
当且仅当θ=时取等号,又则SAEBF=

评注利用向量的正投影解决四边形的面积问题不需要单独处理h1,h2,再进行整合,大大的缩减了运算过程,使得解题变得更加快捷、准确.

三、方法总结

在利用向量正投影解决赛题中的四边形面积最值问题后,笔者发现,该方法可以求任意四边形ABCD的面积,现将其一般步骤总结如下(如图2)：

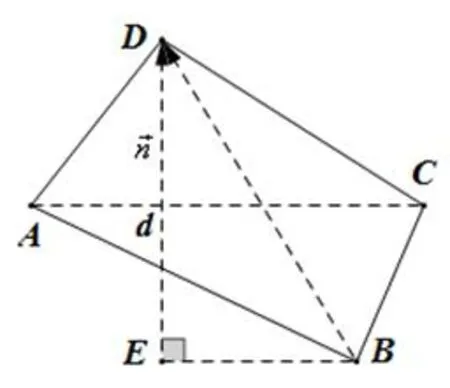
图2

(1)以四边形ABCD的一条对角线(不妨设为AC)为底,计算其长度;

(2)求直线AC的法向量n,一般,若AC的一般方程为：ax+by+c=0(a,b,c∈R),则n=(a,b);

(4)计算四边形ABCD的面积S,即.

利用向量正投影求四边形的面积时,不需要进行分割求和,尤其在求不规则四边形面积时,更能凸显其优势.下面举例说明.

四、应用举例

例 1(2019年高考全国 ⅠⅠⅠ卷第 21题)已知曲线为直线上的动点,过D作C的两条切线,切点分别为A,B.

(1)证明：直线AB过定点;

解(1)设求导得y′=x,所以切线AD的斜率为x1,则整理得

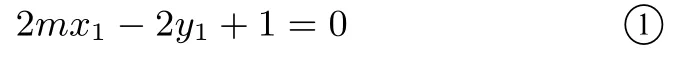
同理可得

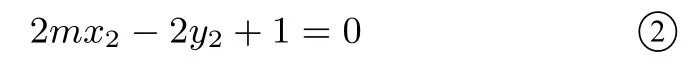
由①②可知AB的方程为2mx-2y+1=0,故直线AB过定点

(2)将直线AB的方程代入抛物线

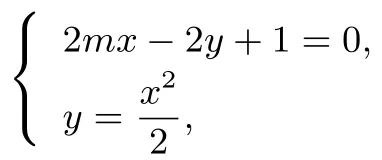
整理得：x2-2mx-1=0.则x1+x2=2m,x1x2=-1.所以

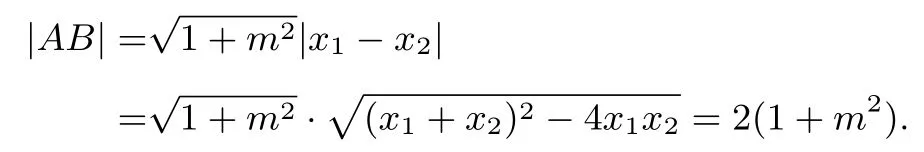
取直线AB的一个法向量n=(m,-1),又则在n上的正投影故四边形ADBE的面积设AB的中点为P,则取AB的一个方向向量n=(1,m),则,整理得m(m2-1)=0,解得m=0或m=±1.当m=0时,S=3;当m=±1时,

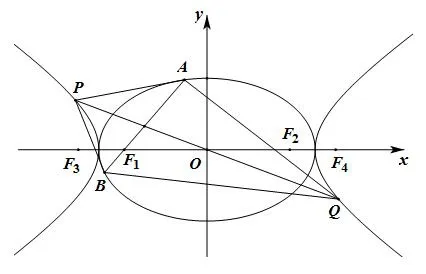
图3

例2(2014年高考湖南卷理科第21题)如图3,O为坐标原点,椭圆C1:的左、右焦点分别为F1、F2,离心率为e1;双曲线的左、右焦点分别为F3、F4,离心率为e2.已知e1e2=,|F2F4|=.

(1)求C1,C2的方程;

(2)过F1作C1的不垂直于y轴的弦AB,M为AB的中点.当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.

解(1)椭圆C1方程为双曲线C2的方程为(过程略).

(2)设A(x1,y1),B(x2,y2),P(x3,y3),Q(-x3,-y3),M(xM,yM),由(1)可得F2(-1,0),因为直线AB不垂直于y轴,所以设直线AB:x=my-1,则y1)=(m(y2-y1),y2-y1),由消x,可得(m2+2)y2-2my-1=0,其中Δ=8m2+1)＞0,

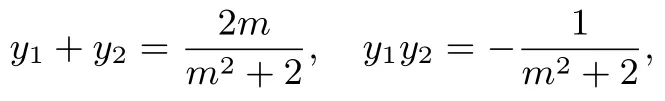
则

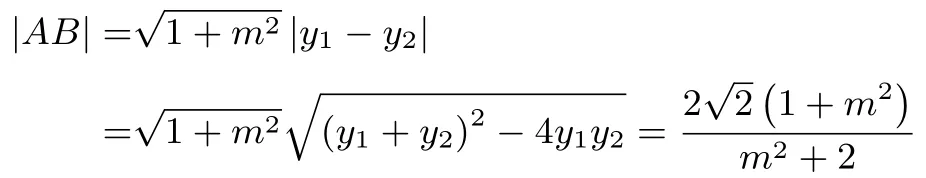
yM=因为点M在直线AB上,所以xM=所以.则直线PQ的方程为y=由消去y,整理得=,其中0＜2-m2≤2.又(2x3,-mx3),取直线AB的法向量v=(1,-m),则点P,Q到AB的距离之和d==.所以四边形APBQ的面积

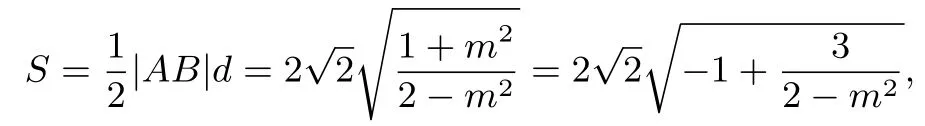
因为0＜2-m2≤2,故当m=0时,Smin=2.综上,四边形APBQ的面积的最小值为2.