探源觅流变中进 进中求通提素养

安徽省池州市第一中学(247000) 吴成强

所谓探源,就是探寻问题的源头,即一类问题的“源题”或“根题”.这个“源题”,它集概念、思想、方法于一身,秀外慧中,堪称经典.它蕴含着巨大的“宝藏”,极具开发价值,能够延伸演变成许多新题、趣题.觅流,就是探寻“源题”所有可能的变式或变化.变中求进,就是推陈出新,创新创造,在深度和广度上进一步发掘,发现和提出更能发人深省、引人入胜、启迪智慧的高质量、高水平问题,促进思维深度发散,增强思维创新活力和张力.进中求通,就是通过变式发散,使学生对问题的理解能够真正做到通晓、通透、通畅,举一反三、触类旁通、融会贯通,最终能够提升数学素养.数学教学中,教师要注重引导学生发掘问题的“根”和“本”,这是一条培养学生善于发现问题、提出问题、分析问题和解决问题的重要渠道,是培养学生“追根究底”良好探究习惯、提升思维品质的重要抓手,是有效解决问题的立足点、着力点、着眼点和生长点.由这个“根”和“本”发展出去,就会延伸和生长出许多新颖有趣的问题,就会枝繁叶茂,百花齐放,五彩缤纷.我们对一些问题的求解,就是要注意从这个问题的“根”和“本”上思考,溯本求源,这样就能从“根本”上找到解决问题的通性通法,就会根据已有的经验快速地解决问题,也会加深我们对数学精髓和本质的理解.数学问题的“根”和“本”是数学问题的内核,是数学问题的“源泉”,对数学问题的求解起着居高临下、统揽全局的作用,达到做一题、习一法、会一类的效果.数学问题的“根”和“本”有些是显性的,有些是隐性的,对数学问题的“根”和“本”进行深度探究,就会使数学学习底蕴深厚、根基牢靠、趣味横生,对激发学生探究欲望,引导学生掌握探究方法,培养学生探究习惯,提高学生探究能力,提升学生数学素养是积极和有效的.

一、“源”于“经典问题”,注重一题多变

数学中有许多经典的例、习题,它们虽自身小巧玲珑,但却内涵丰富,思想活跃,方法独特,给人思维有很大的启迪,让人感到春风拂面,心旷神怡,刻骨铭心.这些经典的例习题,巧妙地将一些重要的知识点融合在一起,它们彼此之间的衔接、过渡、转换是那么的自然,让人感到真是巧夺天工,璞玉天成.这些经典题既能加强对有关数学概念的深刻理解和灵活运用,也能巩固和提高思想方法的灵活运用,同时对思维能力的培养也是落地生根、扎扎实实的.这类题目还深受高考命题者的青睐,通过这类题可以编出许多新颖有趣的“高考题”,使这些高考题源于课本、源于经典,但又高于课本、活于经典.这些“新题”更有趣味性、知识性、方法性、技巧性,使人的思维更加深刻、活跃,视野更加开阔.

例1 (2013年高考辽宁卷文科)已知函数f(x)=则=( )

A.-1 B.0 C.1 D.2

解易知f(x)+f(-x)=0,f(lg2)+=f(lg2)+f(-lg2)=0,故选B.

评注函数是“著名的奇函数”,在资料上随处可见,但大多数学生也只是“做过看过”一带而过,缺乏深入地思考和研究,对其自身隐含的“宝藏”没有及时开发,错失对思维深度、高度和灵性的有效训练.这个函数隐含的性质为奇函数且为增函数.这个问题可称得上是一个很好的“母题”或“根题”或“源题”,透过这道题的表面,我们要更深层次地研究其本质和性质,这样这道题就被“激活”了,其自身潜在的价值就被很好地开发了,其“育智和激趣”功能也被开发了,真正地发挥了这道题应有的价值.函数就是这个“母题”的“变式题”,如果我们能对这个“母题”的性质理解的比较透彻,那么对这个“变式题”的性质也就一眼看出,这道题的求解也就自然就比较容易.另外,lg2与互为相反数,这一点要能看到.我们要对一些典型的基本题要由内而外、多角度、多层次、全方位的加以研究,并在这个基础上进行改编、发掘、延伸、发散,不断增大思维的深度,增强思维的灵性.

变式1已知函数的图像关于某点中心对称,则实数a=_____.

解f(x)=2-log2(=2-log2(+x-1+a-2),将函数f(x)的图像向下平移2个单位,再向左平移1个单位,得到函数联系著名的奇函数就知道a=2.

变式2(2015年高考全国 Ⅰ卷)若函数f(x)=为偶函数,则实数a=_____.

解依题意,为奇函数,联系著名的奇函数就知道a=1.

变式3已知函数f(x)=,计算

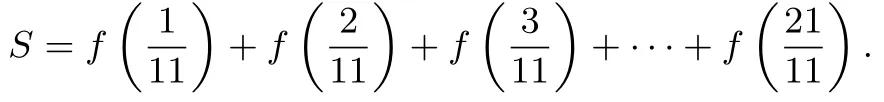
解易知(1,0)是f(x)的对称中心,所以f(x)+f(2-x)=0,所以

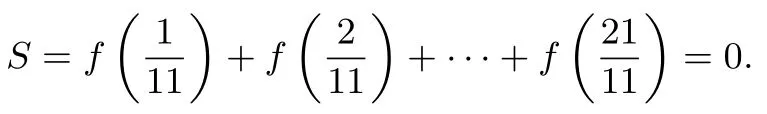
变式4已知函数计算

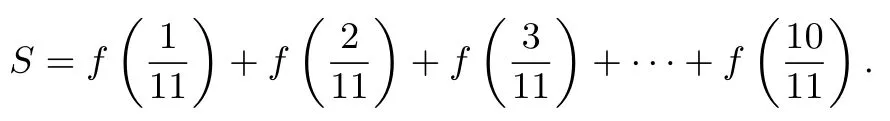
解应该敏锐地观察到首末等距离配对求和,考虑一般情况：f(x)+f(1-x)=1,易知是f(x)的对称中心,易得S=5.

评注“奇函数代表了一切中心对称图形”,当我们遇到函数图像是中心对称图形的时候,就可以“反其道而行之”,将其适当平移后得到一个奇函数,然后利用你对奇函数的经验来处理.

例2已知定义在R上的奇函数f(x)和偶函数g(x)满足,若

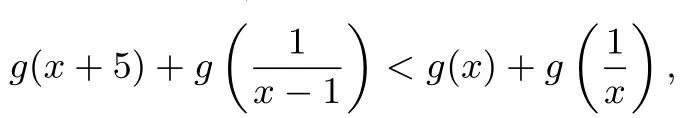
求x的取值范围.

解析由题意得

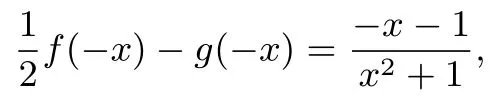
即

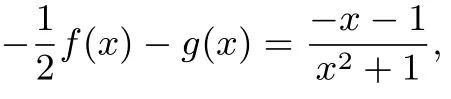
与

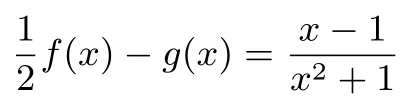
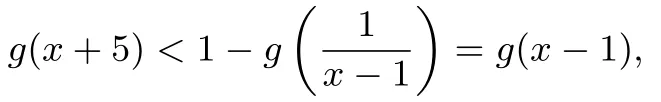
又g(x)为偶函数,故g(|x+5|)＜g(|x-1|),易知g(x)在(0,+∞)上单调递减,故|x+5|＞|x-1|,(x+5)2＞(x-1)2,x＞-2,又所以x＞-2 且x̸=1且x̸=0.

评注定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=h(x),其中h(x)是已知函数,求函数f(x)和g(x),这道题是常见题,可以称得上是一个“母题”或“根题”或“源题”.这道例题就是这个“母题”的“变式题”,并做了进一步的综合和引申.在求出函数g(x)后,进而研究函数g(x)的隐含性质：①g(x)+=1,②在(0,+∞)上单调递减,③偶函数g(x)=g(|x|),综合运用这些性质才能顺利求解,这道题就是对“母题”进行较深的变式.

二、“源”于“数学抽象”,揭示问题本质

有些问题的求解,我们需要撇开问题的表象,抽象出问题的本质,抓住隐含的重要性质,根据这些性质解决这一类问题,这一类问题在形式上可以有很多变化,这就要求对这一类问题隐含的性质透彻理解,并能灵活运用.

例3已知0＜a＜1,设函数

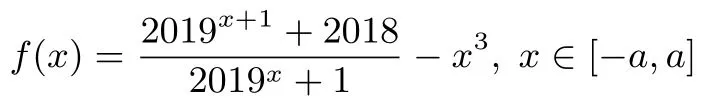
的最大值为M,最小值为m,求M+m的值.

解析

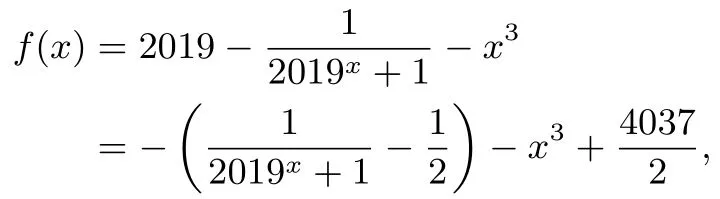
所以M+m=4037.

评注通过分离常数,将函数f(x)配成“著名的奇函数”再利用奇函数性质：奇函数最大值与最小值之和为0,就能顺利求解.这个母题可以延伸改编出很多有价值的“新题”.

例4已知函数f(x)=求不等式的解集.

解易知f(x)定义域为即-1＜x＜1,函数f(x)在定义域(-1,1)上是增函数且为奇函数,原不等式可化为f(x-1)＞f(x2-1),所以

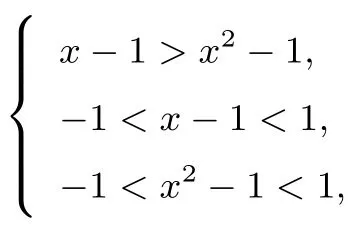
解得0＜x＜1.

评注本题就是抽象出所给函数的奇偶性和单调性这两个重要性质,撇开具体函数解析式的复杂运算,利用性质巧妙求解,这是解决这一类问题的通性通法.

三、“源”于“核心概念”,理解数学精髓

数学的基本框架就是由概念、定义、定理、法则、公式及数学思想和数学方法组成的,数学中的概念、定义、定理、法则、公式是数学中最基础、最重要的“细胞”,是支撑数学学科的“钢梁”,它们之间有着一定的逻辑关系和发展历程,是数学家们艰苦探索和集体智慧的结晶.如果你见到一个数学概念后滔滔不绝如奔涌不息之黄河水,那这个数学概念肯定掌握的比较好.每一个数学概念的学习都要尽可能追求最高境界,突出数学的本质,充分挖掘概念的内涵和外延,掌握相关概念之间的内在联系.例如,有关平面向量的问题,其中“单位向量”和“方向向量”就是“核心概念”,在解决有关向量问题的过程中,如何灵活运用这两个“核心概念”,体现了解题者对向量问题的“精髓”是否有很深的理解,对概念的内在联系和相互转化是否研究透彻、运用娴熟.

例5已知A(3,4),B(5,12),O(0,0),求∠AOB平分线所在直线的方程.

解取OA边上的单位向量e1=,OB边上的单位向量,则

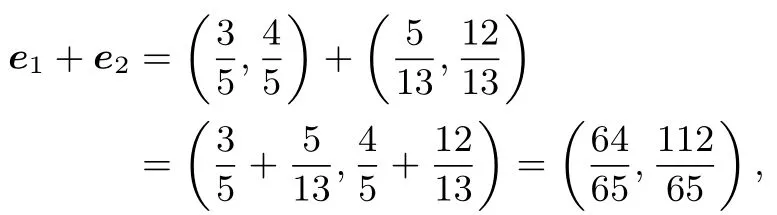
∠AOB平分线所在直线的方向向量为所以∠AOB平分线所在直线的斜率为所以∠AOB平分线所在直线的方程为.

评注本题的解法比较多,但如何简单、快速地解决问题,这是我们需要认真思考和追求的.利用单位向量这个核心概念就可巧妙求解.平面向量基本定理、单位向量、方向向量可以说是平面向量的“三剑客”,“三剑客”是我们求解平面向量问题的利器和法宝.

例6已知O为△ABC所在平面内一点,△OBC,△OAC,△OAB, 的面积分别为S△OBC,S△OAC,S△OAB,求证：.

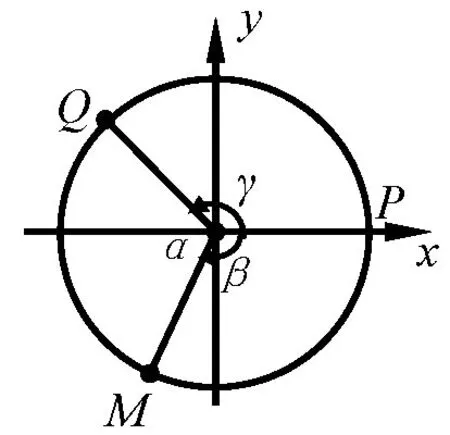
图1

证明设P,Q,M为单位圆O上的三点,均为单位向量,∠QOM=α,∠POM=β,∠POQ=γ,如图1建立平面直角坐标系,设P(1,0),Q(cosγ,sinγ),M(cosβ,-sinβ),(cosγ,sinγ),=(cosβ,-sinβ),

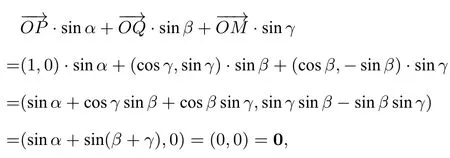
即有

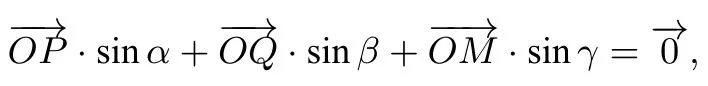
设

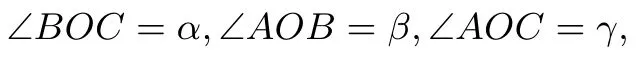
易知

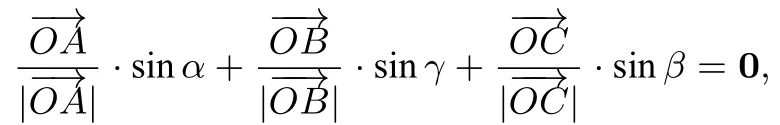
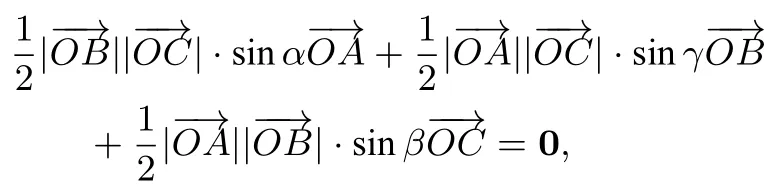
所以

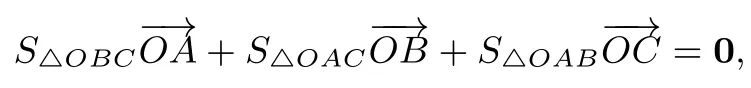
命题得证.

评注本题的结论就是著名的“奔驰定理”,证明就是通过单位向量巧妙求证,再次说明了在解决向量问题时,可以考虑转化为单位向量这个核心概念求解.

四、“源”于“思想方法”,提升思维高度

数学思想方法是数学的“灵魂”,它蕴含在知识发生、发展的过程中,是解决数学问题的“根本大法”.数学思想方法是“纲”,纲举目张.掌握隐含在问题背后的思想方法,就是掌握了解决问题的“万能钥匙”,不管问题形式如何灵活多变,也不管问题求解是否时过多久,只要是掌握了思想方法,那就一定能高屋建瓴,高瞻远瞩,以不变应万变,就能很快找到解决问题的思路,这就是思想方法的魅力所在.所以在解决数学问题过程中,一定要发掘其背后隐含的数学思想方法,不断创新思维方式,转换思维视角,从“根本”上提高解决问题的能力.

例7在数字 1,2,3,···,n(n≥2)的任意一个排列A:a1,a2,a3,···,an中,如果对于i,j∈N∗,i＜j,有ai＞aj,那么就称(ai,aj)为一个逆序对.记排列A中逆序对的个数为S(A).对于数字1,2,3,···,n(n≥2)的一切排列A,求所有S(A)的算术平均值.

解考察排列D:d1,d2,d3,···,dn,与排列D1:dn,dn-1,dn-2,···,d2,d1,因为数对 (di,dj) 与 (dj,di)中必有一个为逆序对,且排列D中的数对(di,dj)共有个,所以S(D)+S(D1)=所以排列D与D1的逆序对的个数的算术平均值为而对于数字 1,2,3,···,n(n≥2)的任意一个排列A:a1,a2,a3,···,an,都可以构造排列A1:an,an-1,an-2,···,a1,且这两个排列逆序对的个数的算术平均值为所以所有S(A)的算术平均值为.

评注本题是一个比较抽象的问题,不少学生看到这个题目有点“晕头转向”,找不着思路,不知如何下手,他们试图把每一个排列的逆序对的个数算出来,再计算算术平均值,这是很困难的一件事,从而导致解不出这道题.本题就是考察学生数学抽象核心素养,要能够灵活转换思维视角,通过引入一个新的排列D:d1,d2,d3,···,dn与排列D1:dn,dn-1,dn-2,···,d2,d1,考察排列D与D1的逆序对的个数的算术平均值,这一思维转换可把问题“解活”了,给人一种超凡脱俗,跳出三界外,不在五行中的感觉,思维顿悟,备受启发,是创新思维最佳生长点,也是破除定势思维和聚敛思维,培养发散思维和求异思维的重要“源头”.

五、“源”于重要的“模型、结论、定理”,提高思维起点

数学中有许多重要的“模型或结论”,它为我们巧妙解决问题搭建了很好的“平台”或“脚手架”,求解问题时如果能恰当利用这些重要“模型或结论”,就会使问题求解变得“程序化”、“模式化”和简单化,从而提高了思维的起点.例如异面直线的计数问题,常常转化为几何体含有多少个三棱锥,再利用每个三棱锥有三对异面直线,就可以轻松求出异面直线有多少对.

例8正方体的8个顶点,任意2个顶点连成一条直线,共可连成28条直线,这28条直线共有多少对异面直线?

解以正方体的顶点为顶点可组成=58个三棱锥,又每个三棱锥有三对异面直线,所以异面直线共有58×3=174对异面直线.

评注本题如果硬数,那就比较麻烦,而且容易出错,利用三棱锥“模型”,既简约思维,又运算简单,所以这个“模型”是我们巧妙解决这类问题的利器.

例9已知不等式xex-a(x+1)≥lnx对x＞0恒成立,求实数a的最大值.

解析由题设易得

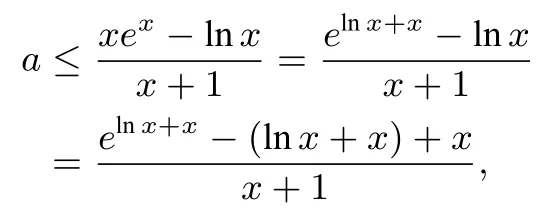
由重要结论ex≥x+1,得

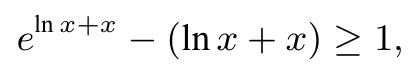
从而

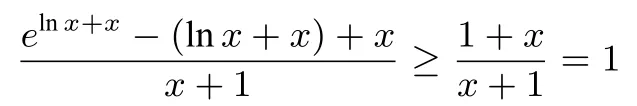
(等号成立的条件是lnx+x=0),所以a≤1,即实数a的最大值为1.

变式已知不等式ax+lnx+1≤xe2x对x＞0恒成立,求实数a的最大值.

解析

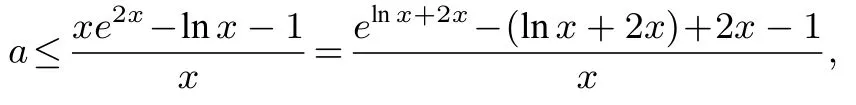
又

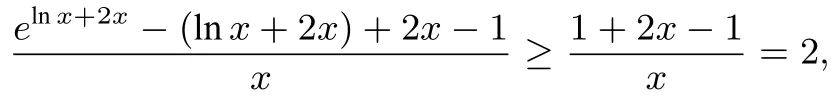
所以a≤2,即实数a的最大值为2.

评注本题求解就是利用重要结论ex≥x+1,使问题求解变得十分巧妙,令人茅塞顿开,颇感震撼,使我们原本感到比较复杂的问题就这样轻轻松松地解决了,真是太巧妙了!再一次显示了重要结论对我们解决有关问题的重要作用,大大地提高了解题的起点,也启迪了我们的智慧,激励我们在数学学习中要勇于探究,不断创新,追求最简、最美的解法.

例10已知N为抛物线x2=4y上一点,A(0,1),M为圆x2+(y-5)2=4上一点,求|MA|+2|MN|的最小值.

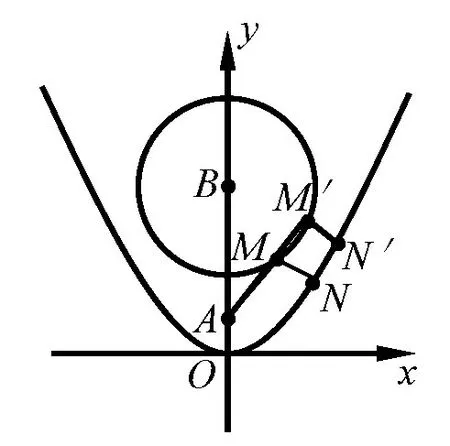
图2

解|MA|+2|MN|=设B(0,b),M(x,y),令,则|MA|=2|MB|,即

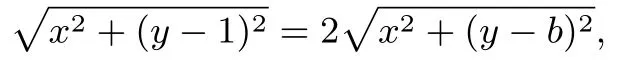
即

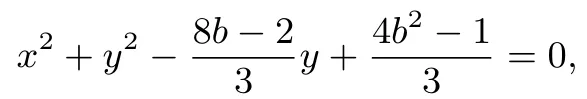
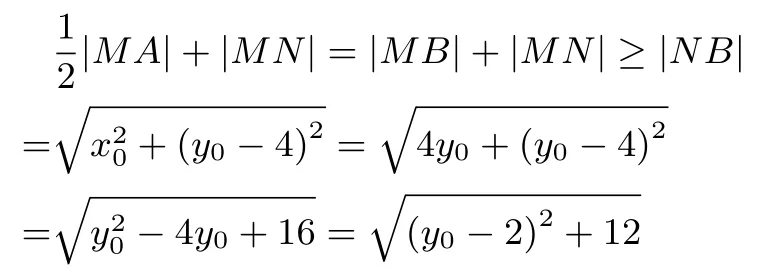
当y0=2,即有最小值的最小值为

评注从教学实践看,多数学生拿到这道题,首先想到用几何的办法来做,但苦于无法转化到“三点共线”,因而用几何办法不得求解,其次尝试利用函数的办法来做,但运算量太大,而且很难算下去,也是不得求解,很多学生对这道题只能是“望题兴叹!”其实,这道题肯定是用几何的办法来做,但需逆用“阿波罗尼斯圆”这个重要定理.阿波罗尼斯圆涉及到两个关键性的点,题目已告诉其中一个关键性的点A(0,1),通过逆用“阿波罗尼斯圆”找到另一个关键性的点B(0,4),然后将|MA|转化到|MB|,就可以利用三点共线最短长度原理轻松求解.

六、“源”于“数学变换”,拓展思维视野

数学变换有很多,例如“同构变换”,“降级变换”,“数形变换”,“齐次变换”,“平移变换”,“伸缩变换”等等,熟练掌握这些变换,并能运用自如,对求解有关问题可以说是如虎添翼,妙不可言,美不胜收.

例11已知四边形EFGH的四个顶点都在椭圆上,且对角线EG,FH过原点O,设EG,FH的斜率分别为k1,k2,若求证：四边形EFGH的面积为定值,并求出此定值.

证明设则x′2+y′2=1,即原来的椭圆压缩为圆,由k1·k2=得所以E′G′⊥F′H′,即四边形EFGH压缩为正方形E′F′G′H′,边长为正方形E′F′G′H′的面积为 2,所以四边形EFGH的面积为

评注本题利用压缩变换,将椭圆压缩为圆,再根据圆的方程求解,运算量降低很多,这种方法具有创造性,拓展了思维视野,对思维有很大的启发性.

七、“源”于“构造”,培养思维创造性

“构造法”本质上就是“无中生有”,它也是求解数学问题最重要、最常用的方法,它的最大特点就是灵活多变,富有创造性,需要解题者有较深的数学功底,要有敏锐的观察力,要把握问题的特点,巧妙地构造出函数或图形,然后巧妙求解.

例 12已知f′(x)=3f(x)+3,f(0)=1,求不等式4f(x)＞f′(x)的解集.

解析令g(x)=则g′(x)==0,所以g(x)=c(c为常数),由f(0)=1得c=2,即g(x)=2,所以f(x)=2e3x-1,原不等式化为f(x)＞3,即2e3x-1＞3,所以

评注本题就是通过构造函数g(x)=巧妙求解,这一构造需要有一定的数学功底以及观察、分析能力,所以在平时的学习过程中要注意多总结、多积累,不断提高创新能力.类似例12的构造函数的方法还有很多,下面再列举几条.

(1)已知f(x)+n+f′(x)＞0,构造函数g(x)=[f(x)+n]·ex.

(2)已知f(x)+n-f′(x)＞0,构造函数g(x)=.

(3) 已知f′(x)+nf(x)＞0,构造函数g(x)=enx·f(x).

(4)已知f′(x)-nf(x)＞0,构造函数g(x)=.

(5)已知f′(x)-nf(x)-n＞0,构造函数g(x)=.

(6)已知f′(x)+nf(x)+n＞0,构造函数g(x)=[f(x)+1]·enx.

在数学学习中,特别是在高三复习中,若能做好探源觅流,变中求进,进中求通,就能使学生跳出“题海”触类旁通;就能使复习做到有力度、有温度、有深度、有广度;就能使复习有主线、有方向、有脉络、有策略,按部就班,有章有法,有条不紊,由浅入深,螺旋上升;就能使学生的思维方式包括全脑思维(左脑的线性思维和右脑的非线性思维)、发散思维、逆向思维、创造性思维得到很好的训练;就能使学生在学习数学、应用数学、探究数学、感悟数学、发现(创造)数学等各种活动中,有意识地、自觉地加以反思,促进其对数学思维活动实现自我察觉、自我评价、自我探究、自我监控、自我调节;就能增强学生发现问题、提出问题、分析问题、解决问题的能力和合作探究的能力,也必然使高三复习基础扎实,思维活跃,能力提升,兴趣盎然,信心倍增,成效明显,学生的学习能力、思维能力和数学素养都得到很大的提升.