含两个绝对值不等式的恒成立问题的研究*

浙江省宁波效实中学(315012) 童益民

文[1]对含一个绝对值不等式的恒成立问题进行了等价性研究,本文试图先通过含两个绝对值不等式的等价变换,转化到含一个绝对值不等式,从而去解决含两个绝对值不等式的恒成立问题.

一、等价性结论

引理1关于x的不等式|f(x)|＜g(x)成立的充要条件是-g(x)＜f(x)＜g(x)成立.

引理2关于x的不等式|f(x)|＞g(x)成立的充要条件是f(x)＞g(x)或f(x)＜-g(x)成立.

结论1关于x的不等式|f(x)|+|g(x)|＜h(x)成立的充要条件是|f(x)+g(x)|＜h(x)且|f(x)-g(x)|＜h(x)成立.

证明根据引理1,

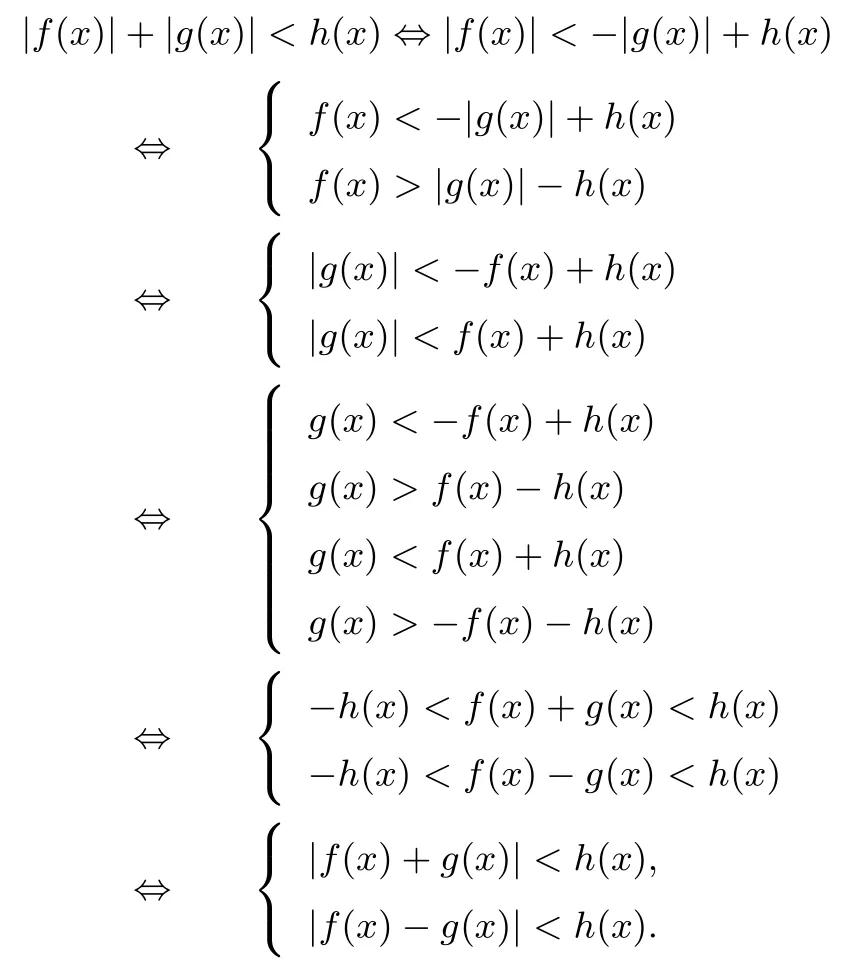
结论2关于x的不等式|f(x)|+|g(x)|＞h(x)成立的充要条件是|f(x)+g(x)|＞h(x)或|f(x)-g(x)|＞h(x)成立.

证明根据引理2,

|f(x)|+|g(x)|＞h(x)⇔|f(x)|＞-|g(x)|+h(x)⇔f(x)＞-|g(x)|+h(x)或f(x)＜|g(x)|-h(x)⇔|g(x)|＞-f(x)+h(x)或|g(x)|＞f(x)+h(x)⇔g(x)＞-f(x)+h(x)或g(x)＜f(x)-h(x)

或g(x)＞f(x)+h(x)或g(x)＜-f(x)-h(x)⇔f(x)+g(x)＞h(x)或f(x)+g(x)＜-h(x)

或f(x)-g(x)＞h(x)或f(x)-g(x)＜-h(x)⇔|f(x)+g(x)|＞h(x)或|f(x)-g(x)|＞h(x).

结论3(1)关于x的不等式|f(x)|-|g(x)|＜h(x)成立的充要条件是|g(x)|＞f(x)-h(x)且|g(x)|＞-f(x)-h(x)成立.

(2)关于x的不等式|f(x)|-|g(x)|＜h(x)成立的充要条件是|f(x)|＜g(x)+h(x)或|f(x)|＜-g(x)+h(x)成立.

证明(1)根据引理1,

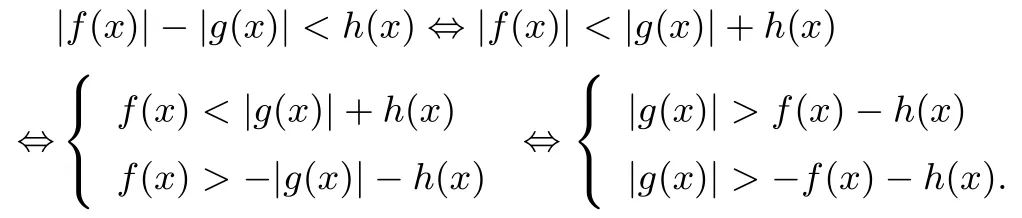
(2)根据引理2,

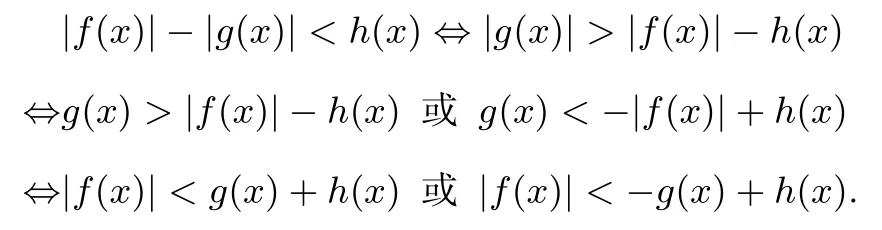
研究关于x的不等式|f(x)|-|g(x)|＞h(x)成立的充要条件,可转化为|g(x)|-|f(x)|＜-h(x),即为结论3的结构.

二、等价性应用

题1已知关于x的不等式对x∈[0,2]恒成立,求实数a的取值范围.

解析根据结论1,因为对x∈[0,2]恒成立,所以10对x∈[0,2]恒成立,所以对x∈[0,2]恒成立且对x∈[0,2]恒成立,所以-10＜x2-2x-2a＜10对x∈[0,2]恒成立,所以x2-2x-2a＞-10对x∈[0,2]恒成立且x2-2x-2a＜10对x∈[0,2]恒成立,所以a＜且a＞-5,所以-5＜a＜.

点题不等式|f(x)|+|g(x)|＜h(x)对x∈D恒成立等价于|f(x)+g(x)|＜h(x)且|f(x)-g(x)|＜h(x)对x∈D恒成立,等价于|f(x)+g(x)|＜h(x)对x∈D恒成立且|f(x)-g(x)|＜h(x)对x∈D恒成立,最后等价于f(x)+g(x)＜h(x)对x∈D恒成立且f(x)+g(x)＞-h(x)对x∈D恒成立且f(x)-g(x)＜h(x)对x∈D恒成立且f(x)-g(x)＞-h(x)对x∈D恒成立,所以解决不等式|f(x)|+|g(x)|＜h(x)对x∈D恒成立问题还是比较容易的.

题2已知关于x的不等式对恒成立,求实数a的取值范围.

解析根据结论2,因为不等式对x∈[0,2]恒成立,所以10对x∈[0,2]恒成立,因为x ∈ [0, 2] 恒成立,所以只能对x∈[0,2]恒成立,根据参考文献[1]的定理1,得x2-2x-2a≥10对x∈[0,2]恒成立或x2-2x-2a≤-10对x∈[0,2]恒成立,所以a≤或a≥5.

点题不等式|f(x)|+|g(x)|≥h(x)对x∈D恒成立等价于|f(x)+g(x)|≥h(x)或|f(x)-g(x)|≥h(x)对x∈D恒成立,其不等价于|f(x)+g(x)|≥h(x)对x∈D恒成立或|f(x)-g(x)|≥h(x)对x∈D恒成立,所以解决不等式|f(x)|+|g(x)|≥h(x)对x∈D恒成立问题是比较麻烦的,为了处理起来容易一点,在出题上会有一定的局限性.

题3已知关于x的不等式对x∈[0,2]恒成立,求实数a的取值范围.

解析根据结论3,因为不等式对x∈[0,2]恒成立,所以且对x∈[0,2]恒成立,所以对x∈[0,2]恒成立,所以对x∈[0,2]恒成立且对x∈[0,2]恒成立,先做对x∈[0,2]恒成立,因为3x≥0,根据参考文献[1]的定理2,得x2-a＞3x对x∈[0,2]恒成立或x2-a＜-3x对x∈[0,2]恒成立,所以或a＞10.再做对x∈[0,2]恒成立,

①当a＜时,因为-x-2a＞0,根据参考文献[1]的定理2,得x2-a＞-x-2a对x∈[0,2]恒成立或x2-a＜x+2a对x∈[0,2]恒成立,所以a＞0或a＞,即a＞0,因为,所以a不存在.

②当a＞10时,因为-x-2a＜0,所以-x-2a恒成立,所以a＞10.

综上：由①②得a＞10.

点题不等式|f(x)|-|g(x)|＜h(x)对x∈D恒成立等价于|g(x)|＞f(x)-h(x)且|g(x)|＞-f(x)-h(x)对x∈D恒成立,也可以等价于|f(x)|＜g(x)+h(x)或|f(x)|＜-g(x)+h(x)对x∈D恒成立,但优先使用等价于|g(x)|＞f(x)-h(x)且|g(x)|＞-f(x)-h(x)对x∈D恒成立,因为后者不容易处理“或”的问题,而前者等价于|g(x)|＞f(x)-h(x)对x∈D恒成立且|g(x)|＞-f(x)-h(x)对x∈D恒成立,可参考文献[1],对|g(x)|＞f(x)-h(x)对x∈D恒成立与|g(x)|＞-f(x)-h(x)对x∈D恒成立分别进行处理,当然对这两个恒成立的处理,可能会遇到一定的难度,为了处理起来容易一点,这时在出题上也会导致一定的局限性.其实不等式对x∈D 恒成立的处理,等价于x2-a＞-x-2a或x2-a＜x+2a对x∈D恒成立,等价于a＞-x2-x或对x∈D恒成立,通过图象可得a＞0,再根据对x∈D恒成立得到的或a＞10,也可得到答案a＞10.

三、总结

对于含两个绝对值不等式的恒成立问题,利用等价变换后是去处理含一个绝对值不等式的恒成立问题,如果先掌握了怎么处理含一个绝对值不等式的恒成立问题,那么处理含两个绝对值不等式的恒成立问题可以变得直接容易一点.对于题1的类型,解题中始终是在处理“且”的恒成立问题,即条件p(x)且条件q(x)恒成立,因为等价于条件p(x)恒成立且条件q(x)恒成立,是比较容易解决的;而对于题2与题3的类型,最后都要处理“或”的恒成立问题,即条件p(x)或条件q(x)恒成立,因为不等价于条件p(x)恒成立或条件q(x)恒成立,处理起来是比较困难的,这时在出题上会有一定的局限性,使解题变得容易一点.这时可能会想到通过条件p(x)或条件q(x)恒成立的否定形式,变为条件非p(x)且条件非q(x)有解,再求其补集,因为其否定形式不等价于条件非p(x)有解且条件非q(x)有解,所以处理起来同样还是很困难的.