与三角形四心相关的一个向量性质

山东省泰安市宁阳第一中学(271400) 刘才华

对于三角形ABC所在平面上一点P,记f(P)=当点P为三角形的四心时,有如下优美而有趣的.

性质在三角形ABC中,G,O,I,H分别为其重心,外心,内心,垂心,则：

(1)f(G)≤f(O)≤f(H);

(2)f(G)≤f(I)≤f(H).

为了行文方便,我们约定△ABC的角A,B,C对应的三边分别为BC=a,CA=b,AB=c,外接圆,内切圆的半径分别为R,r,面积为S,半周长为p.

性质的证明用到如下：

引理1若G为三角形ABC的重心,则f(G)=

证明如图1,设直线AG,BG,CG与对边的交点分别为D,E,F,由

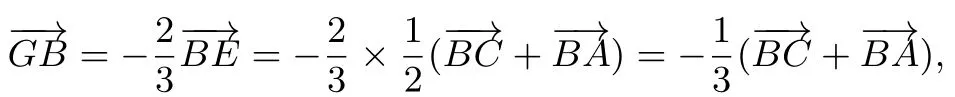
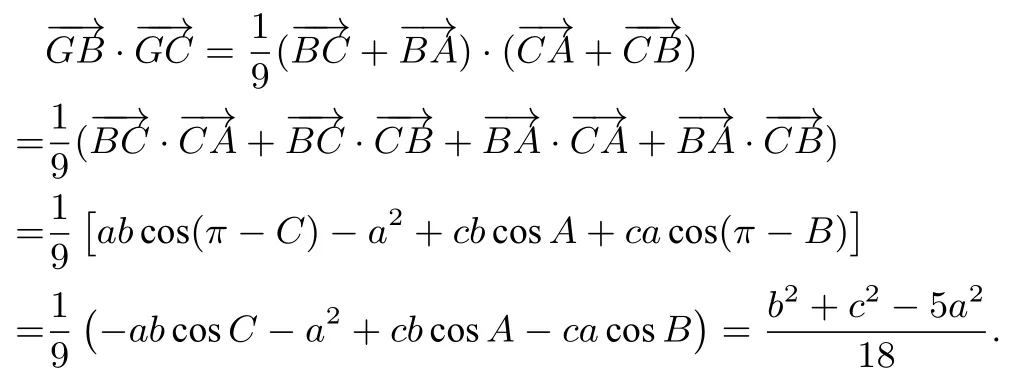
同理

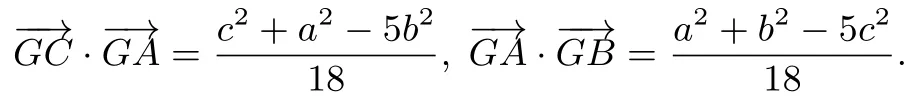
从而

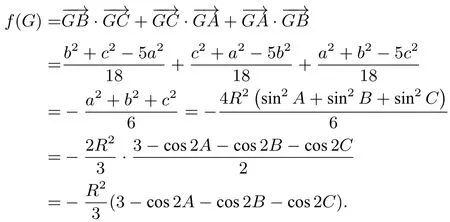
又cos2A+cos2B+cos2C=-1-4cosAcosBcosC,则f(G)=(1+cosAcosBcosC).

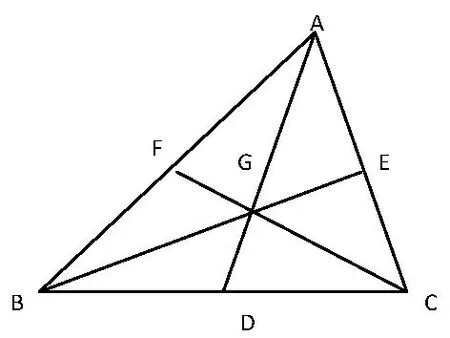
图1

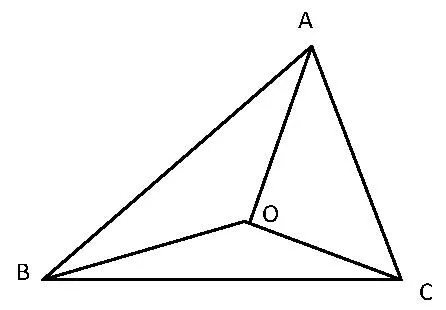
图2

引理2若O为三角形ABC的外心,则f(O)=-R2(1+4cosAcosBcosC).

证明(1)当△ABC为锐角三角形时,如图 2,由∠BOC=2A得同理有R2cos2B,则f(O)=R2(cos2A+cos2B+cos2C).由cos2A+cos2B+cos2C=-1-4cosAcosBcosC得f(O)=-R2(1+4cosAcosBcosC);

(2)当△ABC为直角三角形时,不妨设A为直角,则O为线段BC的中点有f(O)=-R2(1+4cosAcosBcosC);

(3)当△ABC为钝角三角形时,不妨设A为钝角,=R2cos(2C+2B)=R2cos2(π-A)=R2cos2A,有f(O)=-R2(1+4cosAcosBcosC).综上得f(O)=-R2(1+4cosAcosBcosC).

引理3若H为三角形ABC的垂心,则f(H)=-12R2cosAcosBcosC.

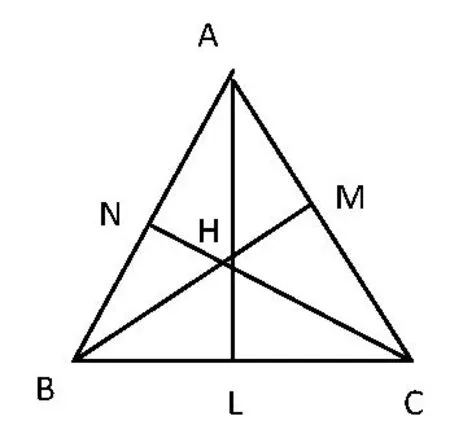
图3

证明(1)当△ABC为锐角三角形时,如图3,设直线AH,BH,CH与对边的交点分别为L,M,N,由三角形的垂心到各顶点的距离与对应顶点内角余弦值的比均等于三角形外接圆的直径得|AH|=2R|cosA|,|BH|=2R|cosB|,|CH|=2R|cosC|.由A,N,H,M四点共圆得∠BHC=∠MHN=π-A,则

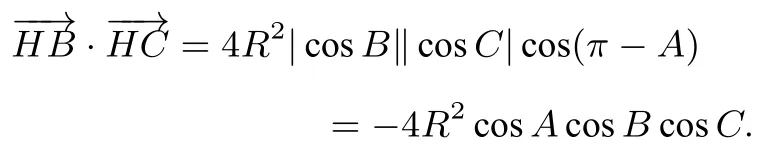
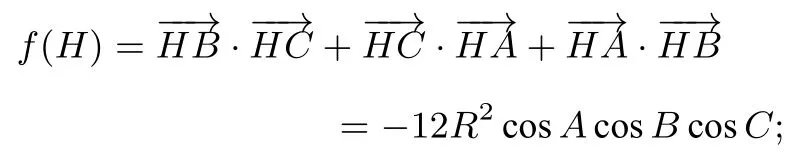
(2)当△ABC为直角三角形时,不妨设A为直角,则H与A重合.0,有f(H)=-12R2cosAcosBcosC;

(3)当△ABC为钝角三角形时,不妨设A为钝角,

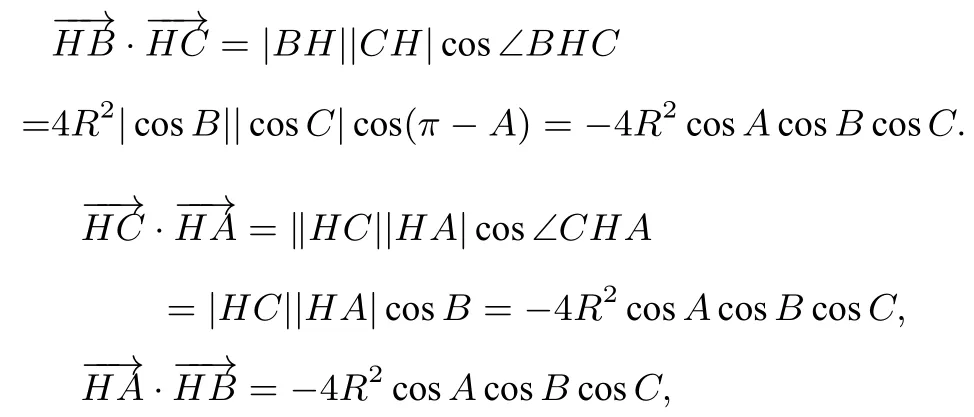
有f(H)=-12R2cosAcosBcosC.综上得f(H)=-12R2cosAcosBcosC.

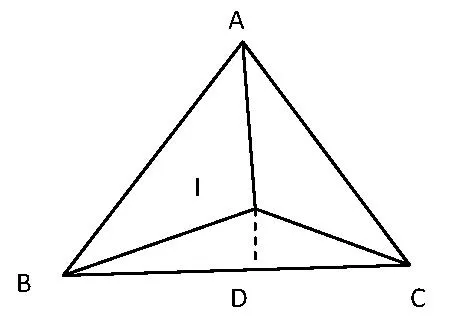
图4

引理4若I为三角形ABC的内心,则f(I)=-2Rr(3-cosA-cosB-cosC).

证明如图4,过点I作ID⊥BC于点D,则由得.

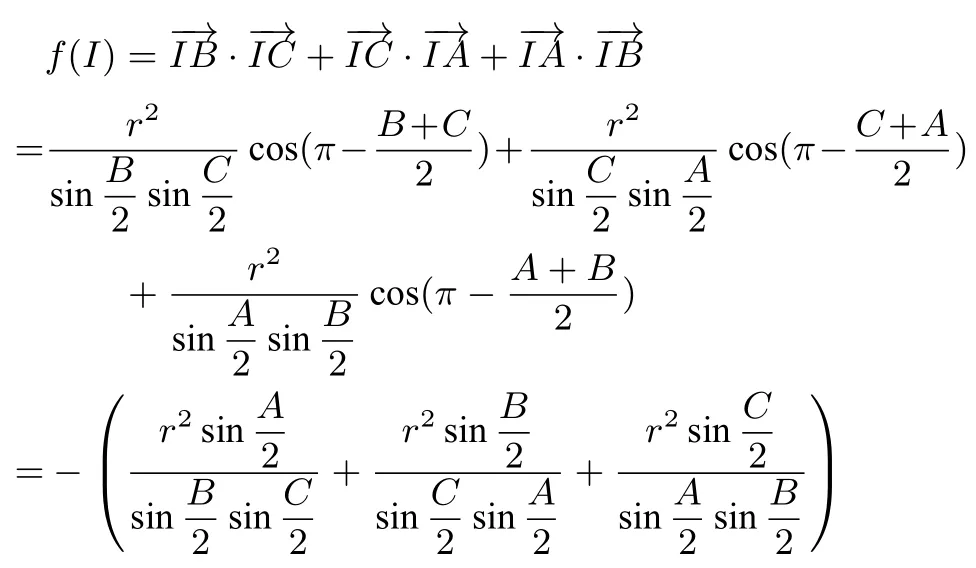
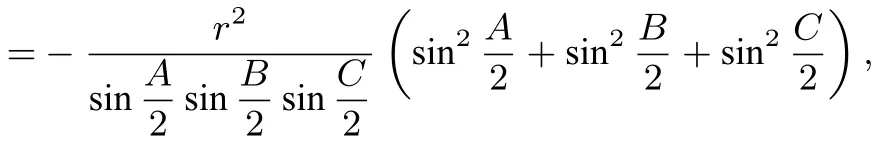
性质的证明(1)由不等式cosAcosBcosC≤得由引理1和引理2得f(G)≤f(O);又由cosAcosBcosC≤得1+4cosAcosBcosC≥12cosAcosBcosC,由引理2和引理3得f(O)≤f(H),于是f(G)≤f(O)≤f(H).

(2)由引理1、引理4及cosAcosBcosC=和得

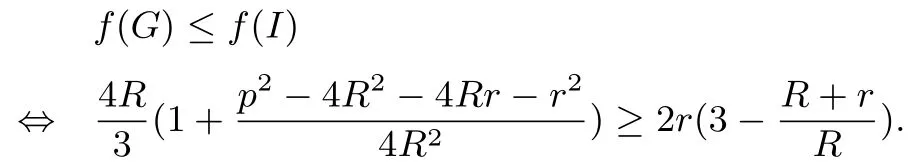
而上述是著名的Gerretsen不等式,从而f(G)≤f(I);又由引理3、引理4及cosAcosBcosC=和cosA+cosB+cosC=得

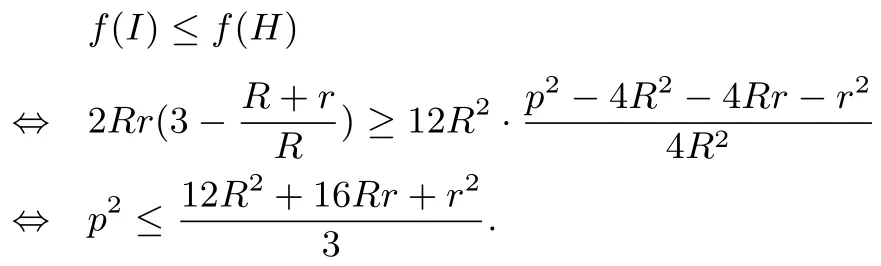
由R≥2r得4R2+4Rr+3r2≤由Gerretsen不等式p2≤4R2+4Rr+3r2得p2≤,所以f(I)≤f(H),故f(G)≤f(I)≤f(H).

但是f(O)和f(I)之间没有大小关系.例如：三角形ABC中,a=3,b=4,c=5,则,cosC=0,从而f(O)=-R2(1+4cosAcosBcosC)=,f(I)=-2Rr(3-cosA-cosB-cosC)=-8,有f(O)＞f(I);由性质证明知f(O)=-R2(1+4cosAcosBcosC)=-(p2-3R2-4Rr-r2),f(I)=-2Rr(3-cosA-cosB-cosC)=-2r(2R-r).三角形ABC中,当b=c=1,a→0时,有f(O)＜f(I).

本文承蒙福建省福州市第二十四中学杨学枝先生的指点帮助,在此致谢.