用构造法证不等式例谈

福建省厦门湖滨中学(361004) 余会昌

不等式证明是高中数学的重要内容,也是教学的一个难点.因为它的证明没有套路,所以在实际证题中,只能根据具体的题目特征采用特定的方法证之.因此,不等式的证明方法五花八门.这里谈谈用构造法来证明不等式.

1.构造公式证明不等式

根据不等式的结构特征,联想到某公式的外形,构造可利用公式的条件来证不等式.

例1已知a,b,c,d∈R,求证：

分析据不等式结构,联想到两点间距离公式,构造可利用这公式的条件.

证明设A(a+c,0),B(0,b+d),C(c,b).由|AC|+|BC|≥|AB|得当且仅当A,B,C三点共线,取“=”.

例2任给7个实数,求证：其中至少有两个数x,y满足.

分析因x,y∈R,从联想到两角差的正切公式,所以,构造符合这个公式的条件来证不等式.

证 明设xi=tanαi(i=1,2,···7) 且把分成六个区间：据抽屉原则,αi(i=1,2,···7)至少有两个角在同一区间,不妨设为α1,α2且α1≥α2,则 0≤α1-α2≤而所以,取x1=x,x2=y,命题得证.当x=y时,左边取“=”;当时,右边取“=”.

2.构造方程证不等式

根据题设特征,构造一元二次方程,利用判别式来证不等式.

例3已知a,b,c∈R,且a+b+c=0,abc=1,求证：a,b,c中必有一个大于.

分析由已知两式,联想韦达定理而构造一元二次方程.

证明由abc=1知,a,b,c中必有一个大于0,不妨设c＞0,因为a+b=-c,所以构造一元二次方程是它的两个实数根,因为a,b,∈R,所以所以c3≥4.因此,

例4在△ABC中,求证：cosAcosBcosC≤.

证明因为cos(A+B)=-cosC=cosAcosB-sinAsinB,cos(A-B)=cosAcosB+sinAsinB,所以cosAcosB=设t=cosAcosBcosC,则有cos2C-cos(A-B)cosC+2t=0,又cosC∈R,所以△=cos2(A-B)-8t≥0,所以8t≤cos2(A-B)≤1,所以t=cosAcosBcosC≤.当A=B=C=60°时,取“=”.

3.构造函数证明不等式

根据要证的不等式的特点,构造出一个函数,利用函数的性质来证明不等式.

例 5设a1,a2,···,an∈R+,求证：对任意的n(n∈N+),

分析待证式具有判别式的模型,所以,构造一个二次函数来证.

证明设f(x)=nx2-2(a1+a2+···+an)x+因为f(x)=(x-a1)2+(x-a2)2+···+(x-an)2≥0对x∈R都成立,所以△=4(a1+a2+···+an)2-≤ 0,即(a1+a2+···+an)2≤当a1=a2=···=an时,取“=”.

例6已知a,b,c∈R+,且abc=8,求证：.

分析待证式左边两式是倒数关系,构造函数f(x)=来证.

证明易证f(x)=x+在[1,+∞)上单调递增,由得当a=b=c=2时,取“=”.

4.构造三角证明不等式

根据题目条件与待证不等式的特点,构造三角函数来证明不等式.

例7已知a,b,c∈R+,且a2+b2=c2,求证：an+bn＜cn(n＞2,n∈N).

证明由题设可知,a,b,c为直角三角形的三边,且c为斜边. 设,因为0＜sinθ＜1,0＜cosθ＜1,所以0＜sinn-2θ＜1,0＜cosn-2θ＜1,即 sinnθ＜sin2θ,cosnθ＜cos2θ,所以an+bn=cn(sinnθ+cosnθ)＜cn(sin2θ+cos2θ)=cn.

例8x,y∈R且满足x2+4y2=4x,求证：2-5≤

证明由x2+4y2=4x,得(x-2)2+4y2=4,这是一个椭圆方程.设x=2+2cosθ,y=sinθ(0≤θ ＜2π)则(其中tanφ=2).所以当 sin(θ+φ)=±1时,取“=”.

5.构造数列证明不等式

根据待证不等式的特点,构造数列,利用数列的增减性来证明不等式.

例9试证：(n≥2,n∈Z).

分析由于待证不等式左边是一个“数列型”,因此,构造数列来证这个不等式.

证明设an=(n≥2,n∈Z),因为,所以数列{an}是递增数列,其最小项所以n≥2,n∈Z时,均有an＞a2＞1,易知原不等式成立.

例10求证：

分析由于不等式左边是个“数列型”,因此,构造数列来证这个不等式.

证明设易知所以{an}是单调递增数列,所以an≥a1==即

6.构造图形证明不等式

根据待证不等式的结构特征,构造出符合不等式中有关式子要求的图形,从而使得不等式得以证明.

例11已知x,y,z∈R+求证：

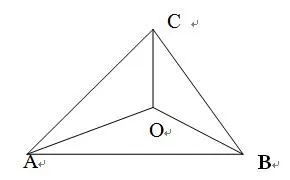
图1

分析不等式两边的三个根式的被开方数类似余弦定理,因此,构造出满足三个式子的图形.

证明作△ABC,如图1,在△ABC内取一点O,使∠AOB= ∠BOC= ∠COA=120°,OA=x,OB=y,OC=z,则AB=AC=因为AB+AC＞BC,所以

例12设a,b,c∈R+,求证：.

图2

证明根据不等式左、右两边的特点,利用勾股定理构造满足条件的图形,如图2,从图中易得要证的不等式.当a=b=c时,取“=”.

7.构造复数证不等式

根据待证不等式的结构特征,构造复数,利用复数的性质来证明不等式.

例13已知a,b,c∈R,求证：.

分析由待证不等式的左边结构,联想到复数的模,因此,构造复数来证明.

证明设z1=a+(1-b)i,z2=b+(1-c)i,z3=c+(1-a)i,z4=1-a+ci,z5=1-c+bi,z6=1-b+ai.则即当a=b=c=时,取“=”.

例14求证：

分析因所以,联想到复数不等式：|z1|+|z2|≥|z1+z2|,构造复数来证不等式.

证明设z1=1+isinx,z2=1+icosx,由|z1|+|z2|≥|z1+z2|(当argz1=argz2时等号成立).所以当时,取“=”.