基数意义下自然数的运算（二）

张新春

基数意义下自然数的运算（二）

张新春

现在小结一下，从加法的定义出发，我们已经知道了加法的两个性质：交换律与结合律。关于加法的所有规律，都可以由此开始通过逻辑推理而获得，下面举一例。

证明：a+b+c=a+c+b。

读者也许会说，这不就是加法交换律吗？只是把c与b的顺序交换一下啊。事实上不是这样的。按定义，a+b+c是（a+b）+c，而a+c+b=（a+c）+b，b与c根本不直接相加，无所谓交换。下面即是这个等式的证明（在阅读这个证明之前，再次提醒读者注意，我们能用来作证明依据的只有几个定义和交换律与结合律而没有别的）。

证：a+b+c=（a+b）+c（三个数相加的定义）

=a+（b+c）（加法结合律）

=a+（c+b）（加法交换律）

=（a+c）+b（加法结合律）

=a+c+b（三个数相加的定义）

这个证明说明，a+b+c=a+c+b成立的原因不仅有交换律，还有结合律。若加法不满足结合律，只满足交换律，我们是无法得到a+b+c=a+c+b的。为了说明这一点，我们再作一点讨论。以下将对运算的意义作些拓展，并构造出一个只满足交换律而不满足结合律的运算。这些讨论属于近世代数（也称抽象代数）的范畴。

我们通常的计算对象是数，计算的方法是加、减、乘、除。但随着数学的进步，人们发现，对很多不是数的对象，同样可以进行类似普通计算方法的计算。这样，我们可以把运算的定义进行一般化。所谓一般的运算，涉及三个集合，不妨记为A，B，C。对A中的任意一个元素a和B中的任意一个元素b组成的元素对（a，b），我们在C中确定一个唯一的元素c与之对应。我们就说是对a和b进行运算，结果是c。

比如设A=｛蓝，红｝，B=｛黄｝，C=｛绿，橙｝，我们规定：

（蓝，黄）→绿

（红，黄）→橙

这就是一个运算。

运算有时也可用一个表来表示，如：

更多时候，我们研究的运算中A，B，C是同一个集合。比如自然数内的加法，就是为两个自然数找一个像，这个像叫做这两个自然数的和。

我们来考虑熟悉的“石头、剪刀、布”游戏。分别用a，b，c表示“石头”、“剪刀”和“布”，于是有a胜b，b胜c，c胜a。

我们规定a和b运算的结果就是它们之间的胜者。同时规定a和自己运算，还得自己。按这样的规则，我们就规定了集合A=｛a，b，c｝内的一个运算，并约定把这个运算记为^，如下表所示：

显然这个运算满足交换律。

同时，我们不难发现，运算^并不满足结合律。比如（a^b）^c=a^c=c，而a^（b^c）=a^b=a，即有（a^b）^c≠a^（b^c），从而^不满足结合律。我们第一次看到了一个只满足交换律但不满足结合律的例子。

此时，a^b^c=a^c=c，而a^c^b=c^b=b，

从而，a^b^c≠a^c^b。

于是，我们知道，a^b^c=a^c^b的获得，不仅要求运算^满足交换律，还要求运算^满足结合律。

当然，在具体教学中，我们不可能要求小学生这么透彻地理解。但作为数学教师，我们应该理解，同时，也应避免让学生判断31+67+19=31+19+67应用了什么运算定律。因为学生往往会认为只运用了交换律，而教师一时也无法跟学生讲清楚（事实上，这道题即取自人教版四年级下册教材，而教学参考书中提供的答案正是运用了加法交换律）。我们对以下的一个例题（人教版数学教材四年级下册）持保留意见。

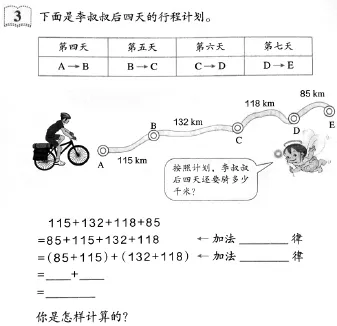
事实上，这里让学生填写用了“加法律”是不合适的。以下一段来源于人教版四年级下册教学参考书。

应当指出的是，在例3的计算过程中：

115+132+118+85=115+85+132+118

把85移到132的前面，严格说来，不仅用到了加法的交换律，还用到了加法的结合律。因为这里之所以能把132+118看作一个整体，之所以能在计算前就先把85与（132+118）交换，都是因为有加法结合律作保证。即：

115+132+118+85

=115+［（132+118）+85］←加法结合律（用了两次）

=115+［85+（132+118）］←加法交换律

=（115+85）+（132+118）←加法结合律

但考虑到小学生的认知特点，只要学生说出第一步运用了加法的交换律把85交换到132的前面，第二步运用了加法的结合律把115与85、132与118结合起来先相加就行了。有些学生常常会省略一些过程，如

115+132+118+85

=（115+85）+（132+118）

或者

115+132+118+85

=200+250

教师都应该给予肯定。

教学参考书上这一段有合理的地方：对每一步运算使用了什么运算定律的解释是正确的。但我们认为，既然由于认知特点的原因，学生尚不能对所用运算定律进行准确的描述，也无法理解这种形式运算，那么我们要求学生判断115+132+118+85= 115+85+132+118这个运算过程中使用了何种运算定律就很不恰当。实际上，教学参考书上说“只要学生说出第一步运用了加法的交换律把85交换到132的前面”，这里所描述的说法恰好是对交换律的误解，交换律不是这么回事。满足于这样的错误说法（不是不严格的说法，而是完全错误的说法）是不恰当的。比较恰当的做法是：学生理解了交换律与结合律后，教师作出概括：根据加法的交换律与结合律，在做连加运算时，加数的顺序与加的顺序都可以是任意的。即先加哪几个，再加哪几个完全是任意的。不再追究每一步到底运用了什么运算定律（或笼统地说成是运用加法交换律与结合律）。同时指出，这个结论以后是可以证明的。事实上，按3个数相加的定义的方式，我们可以定义出4个数、5个数，继而定义出任意多个数相加了。并且，由于加法有交换律、结合律，我们可以任意交换加数的位置（这一点是可以证明的，依据是加法交换律、结合律再加上数学归纳法原理，详细证明这里从略）。