利用导数求解不等式恒成立问题的策略

■河北省秦皇岛市第一中学

含参数的不等式恒成立问题是同学们学习的难点之一,也是高考、数学竞赛的热点,怎样处理这类问题呢? 通过转化能使恒成立问题得到解决,下面就含参数的不等式恒成立问题的解题策略举例说明,以供参考。

一、分离参数法

将原不等式分离参数,转化为不含参数的函数的最值问题,利用导数求该函数的最值,根据要求得出参数的范围。

例1已知函数f(x)=x3-x2+bx+1,若对任意的x∈[0,+∞),都有f(x)≥0恒成立,求b的取值范围。

解析：因为x3-x2+bx+1≥0,所以b≥x-x2-。令g(x)=x-x2-,则当0＜x＜1时,g'(x)＞0;当x＞1时,g'(x)＜0。

故g(x)max=g(1)=-1,b≥-1。

点评： 1.变量与参数的确定：本题x的范围已知,将其视为变量,构造关于它的函数,另一个字母b视为参数。

2.分离参数法遵循两点原则：①已知不等式中两个字母容易进行分离;②分离参数后,已知变量的函数解析式容易求出最值或临界值。

3.一般地,f(x)＞a恒成立,只需f(x)min＞a即可;f(x)＜a恒成立,只需f(x)max＜a即可。

练习1：已知函数f(x)=x3+ax2-2ax+a2,若对任意的x∈(2,+∞),都有f(x)＞a2恒成立,求a的取值范围。

解析：因为当x＞2时,x3+ax2-2ax+a2＞a2,所以令g(x)=当2＜x＜4时,g'(x)＞0;当x＞4时,g'(x)＜0。

故g(x)max=g(4)=-8,a＞-8。

练习2：已知函数f(x)=x3+ax2+9x+a2,若对任意的x∈(0,+∞),都有6xlnx+f'(x)≥0恒成立,求a的取值范围。

解析：因为6xlnx+3x2+2ax+9≥0,所以2a≥-6lnx-3x-

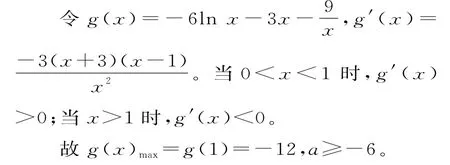
二、函数最值法

将不等式转化为含某个待求参数的函数最值问题,先求该函数的最值,然后构建不等式求解。

例2已知函数f(x)=x3+ax2+bx+a2,当a=0,b=-3时,证明：任意的x∈R,都有恒成立。

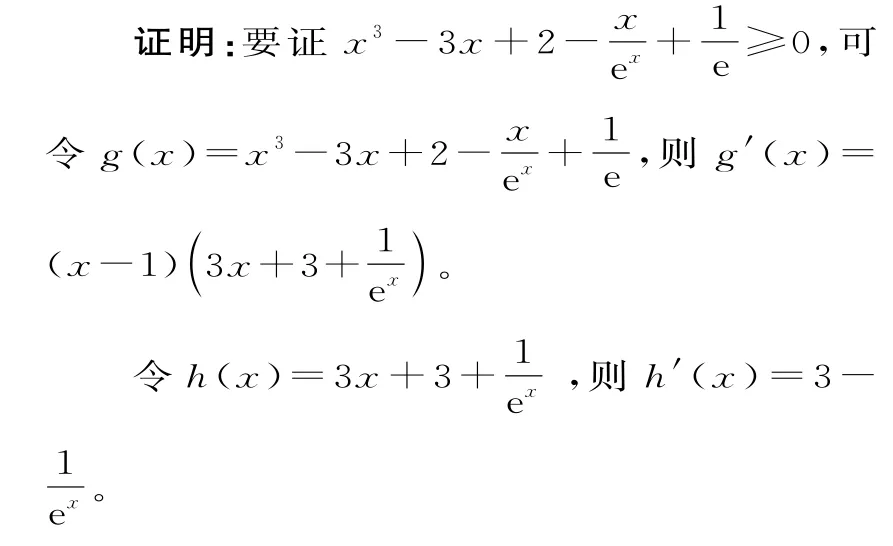
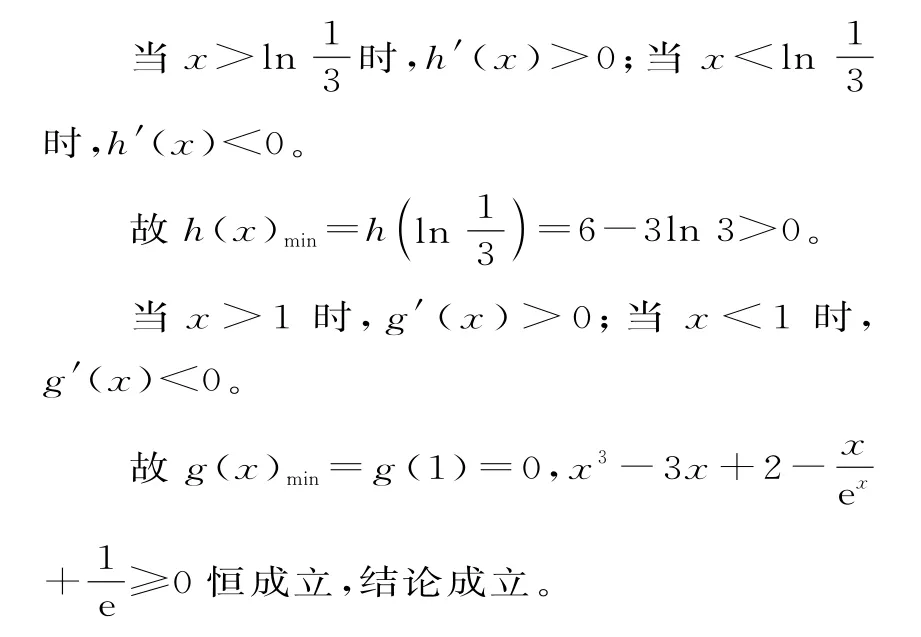
点评： 辨析“f(x)≥g(x) ”型与“f(x1)≥g(x2)”型的差异：

1.对∀x∈I,不等式f(x)≥g(x)恒成立,可转化为求函数[f(x)-g(x)]min≥0。

2.对∀x∈I,不等式f(x1)≥g(x2)恒成立,可转化为求函数f(x)min≥g(x)max。

练习3：已知函数f(x)=x3+ax2+a2,若对任意的x1,x2∈(0,+∞)且x1＜x2都有f(x1)-f(x2)＜a(x1-x2)成立,求a的取值范围。

解析：因为f(x1)-f(x2)＜a(x1-x2),所以f(x1)-ax1＜f(x2)-ax2。

设g(x)=f(x)-ax=x3+ax2-ax+a2,若g(x)在(0,+∞)上单调递增,则g'(x)=3x2+2ax-a≥0对x∈(0,+∞)恒成立。

令h(x)=3x2+2ax-a。

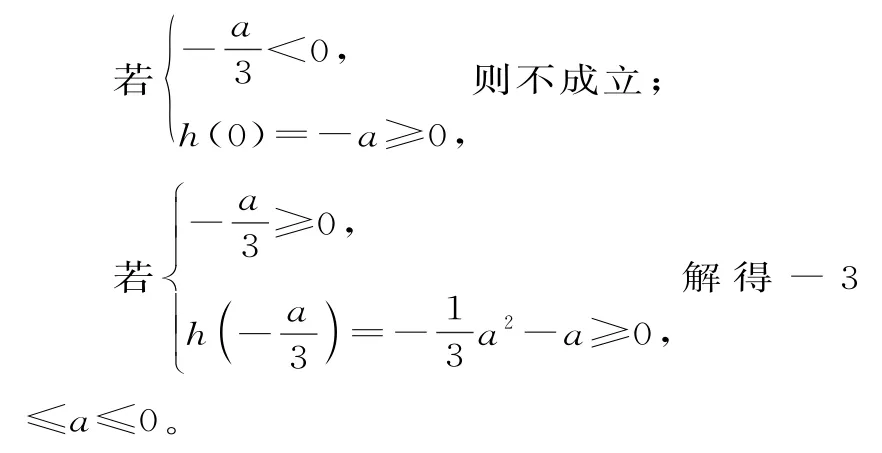
三、分类讨论、放缩取点法

例3已知函数f(x)=x3-x2+bx+1,若∀x∈(-∞,0)都有f(x)≤ex恒成立,求b的取值范围。

解析：ex-x3+x2-bx-1≥0,对∀x∈(-∞,0)恒成立。

令g(x)=ex-x3+x2-bx-1,g'(x)=ex-3x2+2x-b,g'(0)=1-b。

因为当x∈(-∞,0)时,g″(x)=ex-6x+2＞0,所以g'(x)在(-∞,0)上单调递增。

当1-b≤0,即b≥1 时,g'(0)≤0,g'(x)＜0,g(x)在(-∞,0)上单调递减,g(x)＞g(0)=0;

当1-b＞0,即b＜1 时,g'(0)＞0,则∃x0＜0,使得g(x)在(x0,0)上单调递增,但x∈(x0,0)时,g(x)＜g(0)=0,此时不成立。

综上,b≥1。

练习4：(2010年新课标理数)设函数f(x)=ex-1-x-ax2,当x≥0时,f(x)≥0,求a的取值范围。

解析：由题意知f(x)=ex-1-x-ax2且f(0)=0,则∀x∈[0,+∞),f(x)≥f(0)恒成立。

由f'(x)=ex-1-2ax,得f″(x)=ex-2a。易知f″(x)=ex-2a在[0,+∞)上单调递增,f″(x)≥f″(0),即f″(x)≥1-2a。

①当1-2a≥0,即时,由f″(x)≥1-2a≥0,则f'(x)=ex-1-2ax在[0,+∞)单调递增,f'(x)≥f'(0),即f'(x)≥0,f(x)在[0,+∞)上单调递增,也即∀x∈[0,+∞),f(x)≥f(0)符合题意。

②当1-2a＜0,即时,令f″(x)=0,即ex-2a=0,解得x=ln 2a。

当x∈(0,ln 2a)时,f″(x)＜0,f'(x)在(0,ln 2a)上单调递减,f'(x)＜f'(0),即f'(x)＜0,f(x)在(0,ln 2a)上递减,f(0)不是f(x)的最小值,不符合题意。

综上所述,a的取值范围为

小结：求解某些数学问题时,根据问题的条件或目标,可构造一种新的函数关系,使问题在新函数下转化并利用函数的有关性质解决原问题是一种行之有效的解题手段。构造函数法解题是一种创造性思维过程,具有较大的灵活性和技巧性。在运用过程中,应有目的、有意识地进行构造,始终“盯住”要解决的目标。