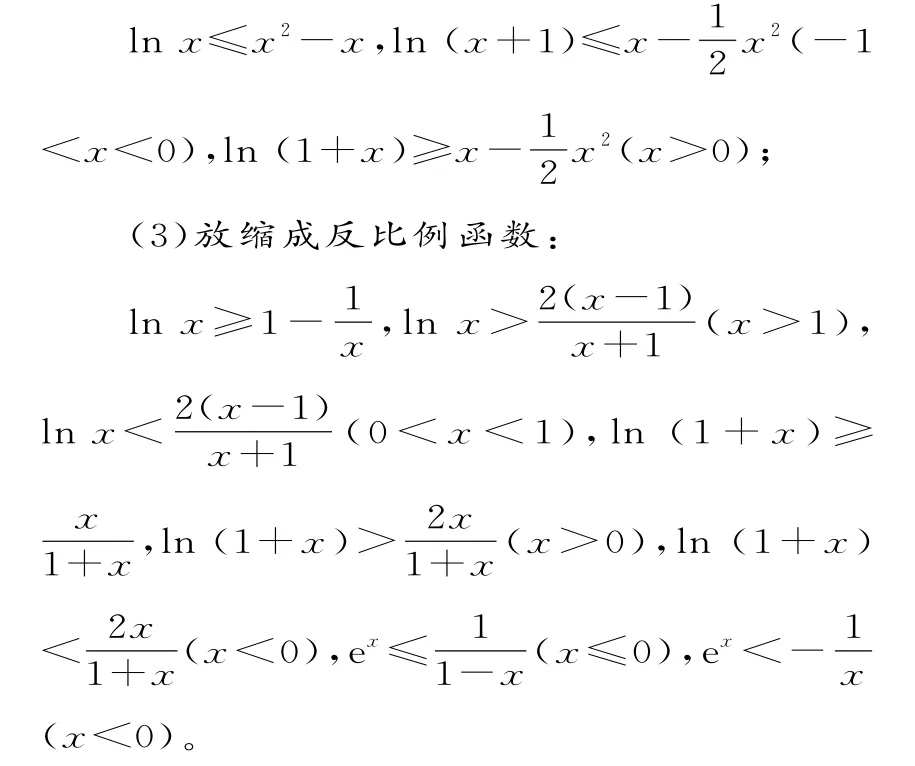求导后,该咋办
■浙江省绍兴市上虞区职教中心
纵观近年来全国各地高考压轴试题,导数解答题以对数函数、指数函数、反比例函数,以及一次函数、二次函数、高次函数中的两个或三个为背景,组成一个具有鲜明特征的超越函数,研究该超越函数性质离不开其单调性,求导也自然成为同学们首要的操作步骤。实际上,我们遇到的函数比较复杂,同学们往往在求导后,不知所措? 下面介绍几种通过求导来求解单调区间的方法,供同学们学习时参考。
一、分解因式
一般地,单调区间的求解过程:已知y=f(x),(1)分析y=f(x)的定义域;(2)求导数y'=f'(x);(3)解不等式f'(x)>0,解集在对应区域内的部分为增区间;(4)解不等式f'(x)<0,解集在对应区域内的部分为减区间。显然,分解因式是求解代数不等式的有力武器。因此,对导函数分解因式是解这类题的首选。
例1(2019 年浙江省高考试题)已知实数a≠0,设函数x>0,当时,求函数f(x)的单调区间。
分析:所给函数比较复杂,可先求出导函数,然后利用常规手段即分解因式解不等式f'(x)>0或f'(x)<0。


表1
所以,函数f(x)的单调递减区间为(0,3),单调递增区间为(3,+∞)。
点评:要顺利求解复杂函数的单调区间,首先必须会准确求解函数的导数,其次要会熟练求解各类不等式:根式不等式、指数不等式、对数不等式。
二、分类讨论
一般地,当导函数中含有参数时,可将问题转化为求解含参不等式,需对参数进行分类讨论。
例2(2019 年高考全国Ⅲ卷理数)已知函数f(x)=2x3-ax2+b。
(1)讨论f(x)的单调性。
(2)是否存在a,b,使得f(x)在区间[0,1]的最小值为-1且最大值为1? 若存在,求出a,b的所有值;若不存在,说明理由。
分析:对函数f(x)=2x3-ax2+b求导,即得f'(x)=6x2-2ax=2x(3x-a),要确定f'(x)>0,需对a分类讨论。
解:(1)f'(x)=6x2-2ax=2x(3xa)。
令f'(x)=0,得x=0或

若a=0,f'(x)在(-∞,+∞)单调递增。

(2)满足题设条件的a,b存在。
(i)当a≤0时,由(1)知,f'(x)在[0,1]上单调递增,所以f'(x)在区间[0,1]上的最小值为f(0)=b,最大值为f(1)=2-a+b。此时a,b满足题设条件当且仅当b=-1,2-a+b=1,即a=0,b=-1。
(ii)当a≥3时,由(1)知,f'(x)在[0,1]上单调递减,所以f'(x)在区间[0,1]上的最大值为f(0)=b,最小值为f(1)=2-a+b。此时a,b满足题设条件当且仅当2-a+b=-1,b=1,即a=4,b=1。
(iii)当0<a<3 时,由(1)知,f'(x)在[0,1]上的最小值为,最大值为b或2-a+b。
综上,当且仅当a=0,b=-1 或a=4,b=1时,f'(x)在[0,1]上的最小值为-1,最大值为1。
点评:分类讨论是一种逻辑方法,是一种重要的数学思想,同时也是一种重要的解题策略,它体现了化整为零、积零为整的思想与归类整理的方法。有关分类讨论思想的数学问题具有明显的逻辑性、综合性、探索性,能训练同学们思维的条理性和概括性。
三、零点法
当不等式f'(x)>0为超越不等式时,可采用零点法即先观察或求出导函数的零点,然后根据导函数的单调性写出f'(x)>0的解集即原函数的单调区间。
例3已知函数f(x)=ex-ln(x+m)。设x=0是f(x)的极值点,求m的值,并讨论f(x)的单调性。
分析:根据x=0是f(x)的极值点确定m值,但发觉不等式f'(x)>0 是超越不等式,即无法求解该不等式,需探究新的方法处理。
解:f'(x)=,由x=0是的极值点,得f'(0)=0,解得m=1。
于是f(x)=ex-ln(x+1),它的定义域为
点评:如果导函数存在零点,但令导函数为零后,出现超越方程,直接求解比较困难,此时可先用特殊值试探出方程的一个根,再通过研究其单调性说明其是唯一的。一般地,当导数式含有lnx时,可试根1,e或等,当导数式含有ex时,可试根1或0等。
四、二次求导
令导函数为零后,出现复杂超越方程,直接求解零点比较困难或能求出特殊零点但不清楚零点个数即确定不了导函数的单调性,可实施二次求导。
例4(2018 年高考全国Ⅲ卷理数改编)已知函数f(x)=(2+x+ax2)ln(1+x)-2x。若a=0,证明:当-1<x<0 时,f(x)<0;当x>0时,f(x)>0。
分析:求导后,f'(x)=ln(1+x)-显然f'(x)>0为超越不等式,虽然可以观察到函数f'(x)的零点,但函数f'(x)的单调性不确定,故需二次求导。
解:当a=0时,f(x)=(2+x)ln(1+x)-2x,f'(x)=ln(1+x)-
设函数g(x)=f'(x)=ln(1+x)-
当-1<x<0时,g'(x)<0;
当x>0时,g'(x)>0。
故当x>-1时,g(x)≥g(0)=0,从而f'(x)≥0,且仅当x=0时,f'(x)=0。所以f(x)在(-1,+∞)上单调递增。
又f(0)=0,故当-1<x<0时,f(x)<0;当x>0时,f(x)>0。
点评:当无法采用零点法时,可对导函数y=f'(x)再次求导,以期求出导数的零点及判断单调性。此时,一定要清楚求导的目的,即利用导数的符号,判断原函数的单调性。
五、设而不求
在解决解析几何问题时,我们常常把题目中某些相关的点的坐标先设出来,但在解题中并不求出它的具体值,只把它作为解题过程中的“桥梁”,使问题快速获解,这便是我们常说的“设而不求”的数学思想。在导函数中,我们如果能确定其零点存在,但又无法用显性的代数式进行表达,即所谓的“隐零点”,则可采用形式上虚设,运算上代换的方法。
例5已知函数f(x)=x+xlnx。
(1)求函数f(x)的图像在点(1,1)处的切线方程;
(2)若k∈Z,且k(x-1)<f(x)对任意x>1恒成立,求k的最大值。
分析:对于(1)直接按切线定义可得。对于(2),恒成立问题首先考虑分离参数,即则只需借助导数求出函数g(x)的最小值,但求导后发现,其导函数对应的方程为超越方程,无法求得极值点和单调区间,解题陷入困境。此时,若果断设函数的极值点,则可“柳暗花明”,豁然开朗。
解:(1)因为f'(x)=lnx+2,所以f'(1)=2。
函数f(x)的图像在点(1,1)处的切线方程y=2x-1。
(2)由(1)知,f(x)=x+xlnx,所以k(x-1)<f(x)对任意x>1恒成立,即k<对任意x>1恒成立。
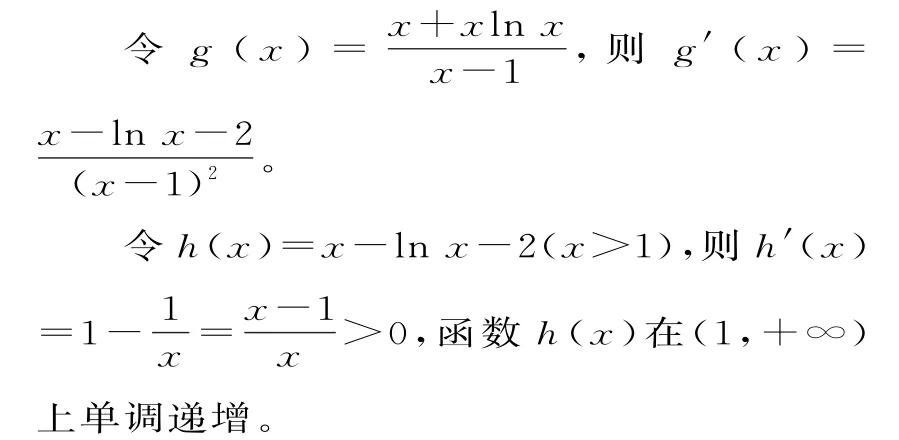
因为h(3)=1-ln 3<0,h(4)=2-2ln 2>0,所以方程h(x)=0 在(1,+∞)上存在唯一实根x0,且满足x0∈(3,4)。
当1<x<x0时,h(x)<0,即g'(x)<0;当x>x0时,h(x)>0,即g'(x)>0。所以函数在(1,x0)上单调递减,在(x0,+∞)上单调递增。

因此,k<[g(x)]min=x0∈(3,4),整数k的最大值是3。
点评:当导函数存在零点,但零点式子非常烦琐或无法求解时,可考虑虚设零点x0,再对f'(x0)=0 进行合理的变形与代换,将超越式化为普通式,从而达到化简f(x0)的目的。
六、不等式放缩
众所周知,如果能顺利求解不等式f'(x)>0(<0),那么导函数的问题都可迎刃而解。因此,将复杂的超越不等式放缩为普通的代数不等式的方法应运而生。
例6设函数f(x)=ex-1-x-ax2。
(1)若a=0,求f(x)的单调区间;
(2)当x≥0时,f(x)≥0,求a的取值范围。
分析:对于(1)直接求导可顺利解得。对于(2),根据ex≥x+1 可得不等式f'(x)≥x-2ax=(1-2a)x,从而可知1-2a≥0,即时,f'(x)≥0,判断出函数f(x)的单调性,得到答案。
解:(1)a=0 时,f(x)=ex-1-x,f'(x)=ex-1。当x∈(-∞,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0。故f(x)在(-∞,0)上单调递减,f(x)在(0,+∞)单调递增。
(2)f'(x)=ex-1-2ax,由(1)可知ex≥1+x当且仅当x=0时等号成立。
故f'(x)=ex-1-2ax≥x-2ax=(1-2a)x,从而当1-2a≥0,即时,f'(x)≥0(x≥0)。而f(0)=0,于是当x≥0时,f(x)≥0。由ex>1+x(x≠0)可得e-x>1-x(x≠0),从而当1-2a<0,即时,f'(x)=ex-1-2ax<ex-1+2a(e-x-1)=e-x(ex-1)(ex-2a)。
故当x∈(0,ln 2a)时,f'(x)<0。而f(0)=0,于是当x∈(0,ln 2a)时,f(x)<0。
综上可得a的取值范围为
点评:由于放缩过程并非等价变换,因此要注意放缩求解的格式。常用的放缩公式有:(1)放缩成一次函数:
lnx≤x-1,lnx<x,ln (1+x)≤x,ex≥x+1,ex>x,ex≥ex;
(2)放缩成二次函数: