全国名校导数测试卷(A 卷)
■河南省汝阳县第一高级中学
一、选择题
1.函数y=f(x)的图像如图1 所示,下列数值排序正确的是( )。
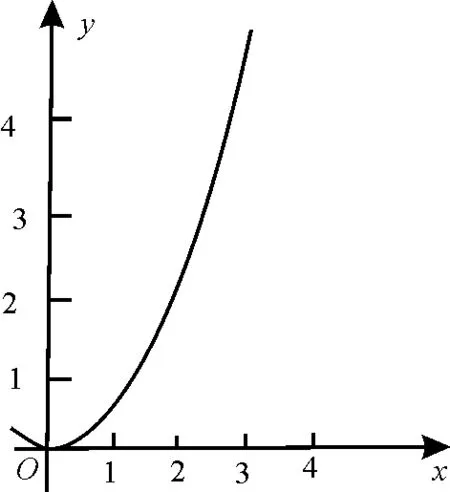
图1
A.f'(1)<f'(2)<f(2)-f(1)
B.f'(1)<f(2)-f(1)<f'(2)
C.f'(2)<f(2)-f(1)<f'(1)
D.f'(2)<f'(1)<f(2)-f(1)
2.曲线y=cosx+ex在x=0处的切线方程是( )。
A.x+y+2=0
B.x-y+2=0
C.x-2y+1=0
D.2x-y+1=0

4.设函数f(x)=alnx+bx2,若函数f(x)的图像在点(1,1)处的切线与y轴垂直,则实数a+b=( )。
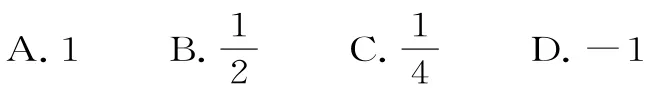
5.对于函数y=ex,曲线y=ex在与坐标轴交点处的切线方程为y=x+1,由于曲线y=ex在切线y=x+1的上方,故有不等式ex≥x+1。类比上述推理:对于函数y=lnx(x>0),有不等式( )。
A.lnx≤x-1(x>0)
B.lnx≥x+1(x>0)
C.lnx≥x-1(x>0)
D.lnx≤1-x(x>0)
6.若函数y=f(x)的图像上存在不同的两点,使得函数y=f(x)的图像在这两点处的切线互相平行,则称函数y=f(x)具有“同质点”。给出下列四个函数:①y=sinx;②y=ex;③y=x3;④y=lnx。其中具有“同质点”的函数有( )。
A.1个 B.2个
C.3个 D.4个
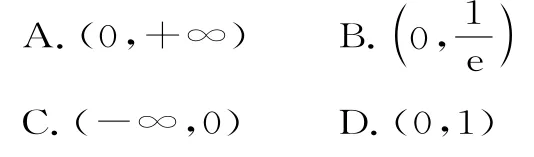
A.(1,+∞) B.[1,+∞)
C.(1,2) D.[1,2]
9.已知实数a,b满足a2-3lna-b=0,c∈R,则(a-c)2+(b+c)2的最小值为( )。

10.已 知f(x)= (lnx)2-,恰有3个不同零点,则a的值为( )。

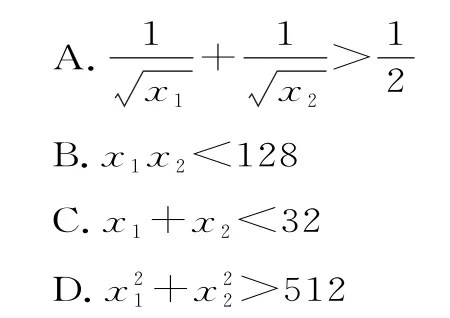
12.已知曲线f(x)=2lnx+ax2+bx在点(1,f(1))处的切线方程为y=x-3,则函数f(x)的零点所在的大致区间为( )。
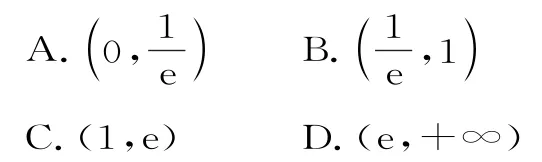
13.关于x的方程kx=sinx(k∈(0,1))在(-3π,3π)内有且仅有5个根,设最大的根是α,则α与tanα的大小关系是( )。
A.α>tanαB.α<tanα
C.α=tanαD.以上都不对
14.若f(x)+3f(-x)=x3+2x+1对x∈R 恒成立,则曲线y=f(x)在点(1,f(1))处的切线方程为( )。
A.5x+2y-5=0
B.10x+4y-5=0
C.5x+4y=0
D.20x-4y-15=0
15.过点P(2,-6)作曲线f(x)=x3-3x的切线,则切线方程为( )。
A.3x+y=0或24x-y-54=0
B.3x-y=0或24x-y-54=0
C.3x+y=0或24x-y+54=0
D.24x-y-54=0
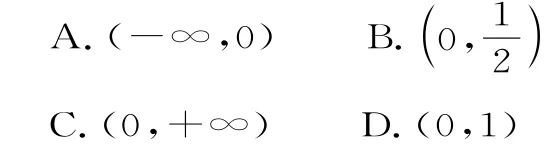
A.(e2,+∞) B.(1,+∞)
C.(1,e2) D.(0,1)
18.已知函数f(x)=ex+x2+lnx与函数g(x)=e-x+2x2-ax的图像上存在关于y轴对称的点,则实数a的取值范围为( )。
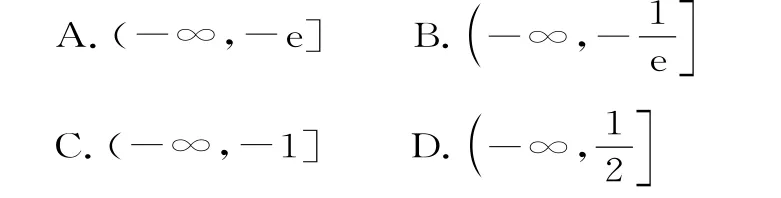
19.已知函数f(x) =若函数g(x)=f(x)-ax+a存在零点,则实数a的取值范围为( )。
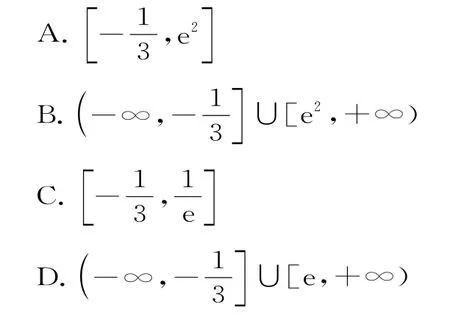
20.设函数y=ax2与函数y=的图像恰有3个不同的交点,则实数a的取值范围为( )。
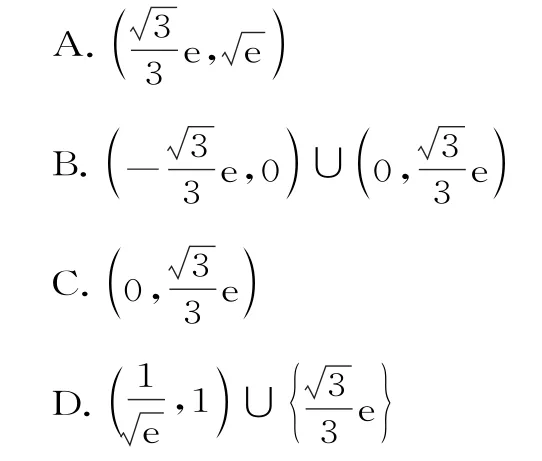
21.设点P,Q分别是曲线y=xe-x(e是自然对数的底数)和直线y=x+3 上的动点,则P,Q两点间距离的最小值为( )。


22.已知y=f(x)(x∈R)存在导函数,若f(x)既是周期函数又是奇函数,则其导函数( )。
A.既是周期函数又是奇函数
B.既是周期函数又是偶函数
C.不是周期函数但是奇函数
D.不是周期函数但是偶函数
23.设点P在曲线y=lnx上,点Q在曲线上,点R在直线y=x上,则|PR|+|RQ|的最小值为( )。
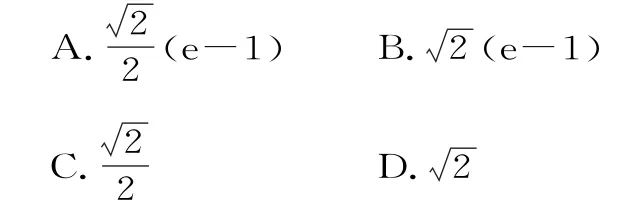
24.已知函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,则实数m的取值范围是( )。
A.(-1,2)
B.(-∞,-3)∪(6,+∞)
C.(-3,6)
D.(-∞,-1)∪(2,+∞)
25.如图2,可导函数y=f(x)在点P(x0,f(x0))处的切线方程为y=g(x),设h(x)=g(x)-f(x),h'(x)为h(x)的导函数,则下列结论中正确的是( )。
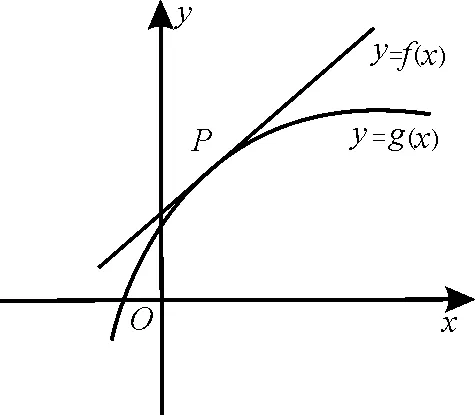
图2
A.h'(x0)=0,x0是h(x)的极大值点
B.h'(x0)=0,x0是h(x)的极小值点
C.h'(x0)≠0,x0不是h(x)的极值点
D.h'(x0)≠0,x0是h(x)是的极值点
26.下列函数中,既是奇函数又存在极值的是( )。

27.设f(x),g(x)分别是定义在R 上的奇函数和偶函数,且f'(x),g'(x)分别是f(x),g(x)的导数,当x<0时,f'(x)g(x)+f(x)g'(x)>0 且g(6)=0,则不等式f(x)g(x)<0的解集是( )。
A.(-6,0)∪(6,+∞)
B.(-6,0)∪(0,6)
C.(-∞,-6)∪(0,6)
D.(-∞,-6)∪(6,+∞)
28.设定义在R 上的函数f x()的导函数为f'(x),若f(x)+f'(x)>2,f(0)=2 020,则不等式exf(x)>2ex+2 018(其中e为自然对数的底数)的解集为( )。
A.(0,+∞)
B.(2 018,+∞)
C.(2 020,+∞)
D.(-∞,0)∪(2 018,+∞)

30.设a=sin 1,b=2sin,c=3sin则( )。
A.a<b<cB.a<c<b
C.c<a<bD.c<b<a
31.已知函数f(x)=ex(x-aex)恰好有两个极值点,则a的取值范围是( )。
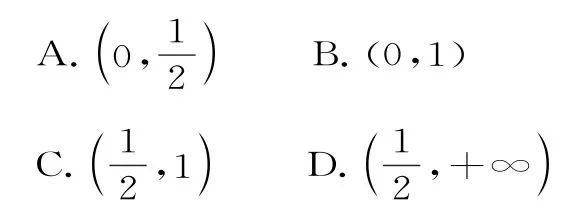
32.已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )。
A.(1,+∞) B.(2,+∞)
C.(-∞,-1) D.(-∞,-2)
33.已知f(x)=x+1,g(x)=lnx,若f(x1)=g(x2),则x2-x1的最小值为( )。
A.1 B.2
C.2-ln 2 D.2+ln 2
34.已知函数f(x)=x2·e-x,g(x)=,若∀x1∈(0,+∞),∃x2∈[1,3],使f(x1)=g(x2)成立,则c的取值范围是( )。

35.已知,若存在α∈M,β∈N,使|α-β|<n,则称函数f(x)与g(x)互为“n度零点函数”。若f(x)=32-x-1与g(x)=x2-aex互为“1度零点函数”,则实数a的取值范围为( )。
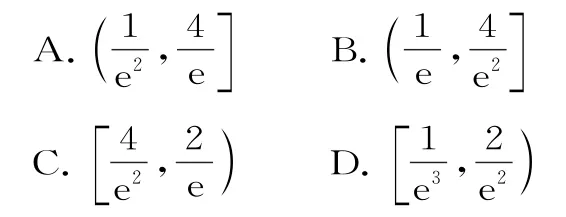
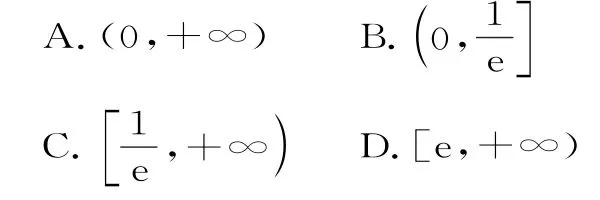
二、填空题
37.图3是函数y=f(x)的导函数y=f'(x)的图像,给出下列命题:
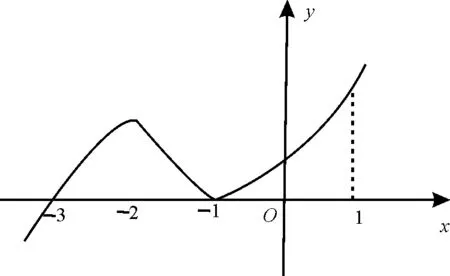
图3
①-3 是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增。
则正确命题的序号是____。
38.函数f(x)=-x2+ax-lnx(a∈R)。则“函数f(x)既有极大值又有极小值”的充要条件为_____。
39.若函数f(x)=(lnx-ax)lnx-x2存在三个不同零点,则实数a的取值范围是____。
40.已知函数y=ex上任意一点P(x0,),在P点处的切线l1交x轴于点A,l2过点P且l1⊥l2,l2与x轴交于点B,则线段AB的长度的取值范围为____。
42.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f'(x),且有3f(x)+xf'(x)>0,则不等式(x+2 019)3f(x+2 019)+27f(-3)>0的解集是____。
46.函数f(x)=(x2-x-1)ex(其中e=2.718…是自然对数的底数)的极值点是____;极大值=____。
47.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”。若f(x)=xlnx与在[1,3]上是“关联函数”,则实数m的取值范围是_____。
48.要设计一个容积为π 的下端为圆柱形、上端为半球形的密闭储油罐,已知圆柱侧面的单位面积造价是下底面积的单位面积造价的一半,而顶部半球面的单位面积造价又是圆柱侧面的单位面积造价的一半,储油罐的下部圆柱的底面半径R=_____时,造价最低。
49.将一边长为a的正方形铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖的方盒,当x等于____时,方盒的容积最大。
51.函数f(x)的定义域和值域均为(0,+∞),f(x)的导数为f'(x),且2f(x)<f'(x)<3f(x),则的范围是____。
52.已知函数f(x)=3x3-2x+ex-其中e 是自然对数的底数,若f(a)+f(a2-2)<0,则实数a的取值范围是____。
53.若函数f(x)=kx-ex有零点,则k的取值范围为____。
54.已知函数f(x)=ex-ax有两个零点x1,x2,则下列判断:①a<e;②x1+x2<2;③x1·x2>1;④有极小值点x0,且x1+x2<2x0。则正确判断的个数是____。
55.形如f(x)=ax3+bx2+cx+d(a≠0)的函数,其图像对称中心为M(x0,f(x0)),记函数f(x)的导函数为f'(x),f'(x)的导函数为f″(x),则有f″(x0)=0。若函数f(x)=x3-3x2+1,则
三、解答题
57.已知a>0,函数f(x)=xlnxax+1+a(x-1)2,g(x)=
(1)求g(x)的单调区间;
(2)讨论f(x)零点的个数。
58.已知f(x)=ax-1-xlnx(a∈R)。
(1)若f(x)≤0恒成立,求a的取值范围;
(2)证明:当x>1时
(1)求f(x)的单调区间;
(1)试比较2 0182019与2 0192018的大小,并说明理由;
(2)若函数g(x)=f(x)-k有两个不同的零点x1,x2,证明:x1·x2>e2。
61.已知函数f(x)=ln(x+1)。
(1)设y=g(x)是函数f(x)在(0,0)处的切线,证明:f(x)≤g(x);
62.已知函数f(x)=e1-x(-a+cosx),a∈R 。
(1)若函数f(x)在[0,π]内存在单调递增区间,求实数a的取值范围;
63.已知函数f(x)=x2(6lnx-4x+6a-3)有两个极值点。
(1)求a的取值范围;
(2)设x1,x2(x1<x2)是f(x)的两个极值点,证明

