向量法解高考中的立体几何问题
■湖北省仙桃八中
向量融数形于一体,具有代数形式和几何形式的“双重身份”,既有有向线段表达式,又有坐标表达式。向量是解决立体几何问题的重要工具,很多立体几何高考题都可以用空间向量找到巧妙的解决方法。现以高考题为例加以说明。
一、向量基底法
在解决立体几何问题时,若不能(或不方便)建立空间直角坐标系,则可采用“向量基底法”,选取恰当的基底,并用它们表示指定的向量,再利用向量的运算,求角和距离,以及证明平行和垂直。向量基底法可作空间向量坐标法的一个补充,掌握该法可有效提高空间向量解立几问题的效率。
1.求异面直线所成角
例1已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )。
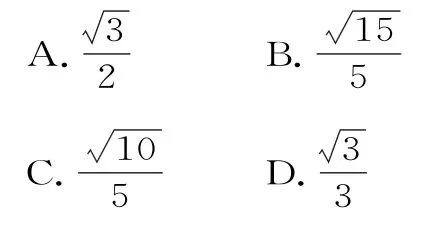



图1
所以异面直线AB1与BC1所成角的余弦值为,故选C。
评注:选取一组基底,将异面直线所成的角转化为用基底表示的向量的夹角或补角,避免找平面角的麻烦。
例2如图2,已知平面四边形ABCD,AB=BC=3,CD=1,AD=∠ADC=90°。沿直线AC将△ACD翻折成△ACD',直线AC与BD'所成角的余弦的最大值为____。
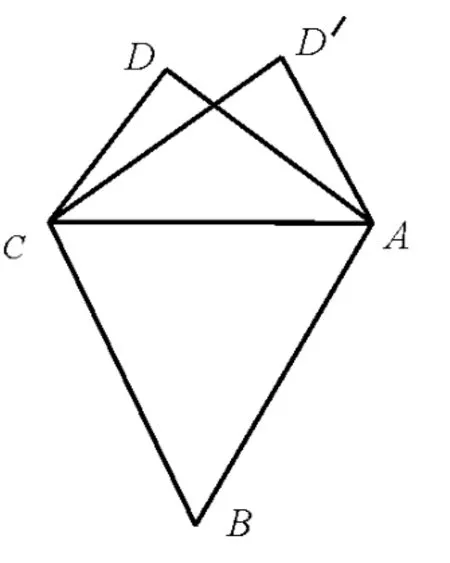
图2

评注:一般尽量选取模长以及两两夹角已知的三个不共面向量作为基底。本题通过引入辅助角(设∠BCD'=θ),结合向量的基本运算,将直线AC与BD'所成角的余弦值表示为关于θ的三角函数求其最值,构思巧妙,解法流畅。
2.求解垂直问题
例3如图3,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点。如图4,现将△AFD沿AF折起,使平面ABD⊥平面ABC。在平面ABD内过点D作DK⊥AB,K为垂足。设AK=t,则t的取值范围是____。
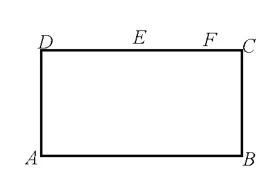
图3
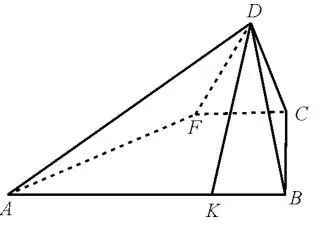
图4

3.处理存在性问题
例4如图5,已知平行六面体ABCDA1B1C1D1的底面为菱形,且∠C1CB= ∠C1CD=∠BCD=60°。

图5
(1)证明:CC1⊥BD。


二、向量坐标法
向量坐标法克服传统立体几何解决问题带来的高度的技巧性和随机性,向量法可操作性强——运算过程公式化、程序化,有效突破立体几何学习难点,是处理立体几何高考题的首选方法。
1.求直线与平面所成的角
例5如图6,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC= 90°,∠BAC=30°,A1A=A1C=AC,E,F分别为AC,A1B1的中点。

图6
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值。
解析:(1)连接A1E。因为A1A=A1C,E是AC的中点,所以A1E⊥AC。又平面A1ACC1⊥平面ABC,A1E⊂平面A1ACC1,平面A1ACC1∩平面ABC=AC,所以A1E⊥平面ABC。如图7,以E为原点,分别以射线EC,EA1为y轴,z轴的正半轴,建立空间直角坐标系E-xyz。不妨设AC=4,则,得EF⊥BC。
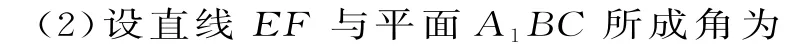


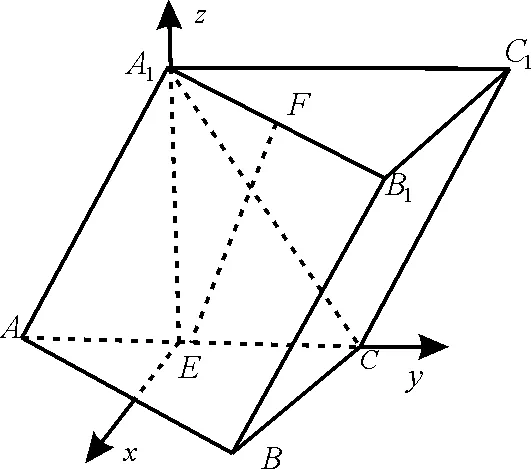
图7
评注:求解直线和平面所成角,要注意直线的方向向量与平面法向量夹角与所求角之间的关系,线面角的正弦值等于两个向量夹角的余弦值的绝对值。
2.求二面角
例6如图8,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别为BC,BB1,A1D的中点。
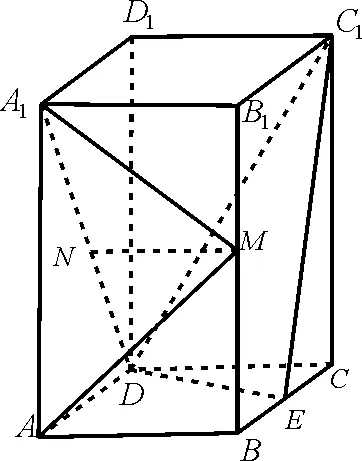
图8
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值。
解析:(1)连接B1C,ME。因为M,E分别为BB1,BC的中点,所以ME∥B1C,且。又因为N为A1D的中点,所以。由题设知,可得,故。因此四边形MNDE为平行四边形,MN∥ED。又MN⊄平面EDC1,所以MN∥平面C1DE。
(2)由已知可得DE⊥DA。以D为坐标原点,的方向为x轴的正方向,建立如图9所示的空间直角坐标系D-xyz,则A(2,0,m=(x,y,z)为平面A1MA的法向量,则所以可取。设n=(p,q,r)为平面_A1MN的法向量,则可取n= (2,0,-1),于是cos

图9
评注:(1)求二面角最常用方法就是分别求出二面角的两个半平面的法向量,然后通过求两个法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角。
(2)利用法向量求二面角大小关键是确定平面的法向量,其方法有两种:①求平面垂线的方向向量;②利用法向量与平面内两个不共线向量的数量积为零,列方程组求解。
3.求点到平面的距离
例7在四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD,PC的中点。
(1)求证:DE∥平面PFB;
(2)求点E到平面PFB的距离。
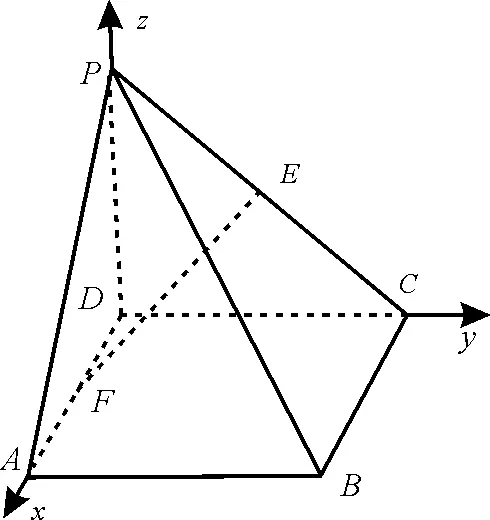
图10
解析:(1)以D为原点,建立如图10 所示的空间直角坐标系,则P(0,0,2),F(1,0,0),B(2,2,0),E(0,1,1)。于是1,1)。所以平面PFB。又因为DE⊄平面PFD,所以DE∥平面PFB。
(2)因为DE∥平面PFB,所以点E到平面PFB的距离等于点D到平面PFB的距离。
设平面PFB的一个法向量n=(x,y,z),则令x=2,得y=-1,z=1,所以n=(2,-1,1)。
因为DE∥平面PFB,所以点E到平面PFB的距离为
评注:求解点到平面的距离可直接转化为向量在平面的法向量上的射影的长。设P在平面α外,n为平面α的法向量,在平面α内任取一点Q,则点P到平面α的距离d=
4.解与平行有关的探索性问题
例8如图11,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=
(1)求证:PD⊥平面PAB。
(2)求直线PB与平面PCD所成角的正弦值。
(3)在棱PA上是否存在点M,使得BM∥平面PCD? 若存在,求的值;若不存在,请说明理由。
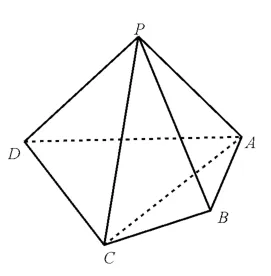
图11
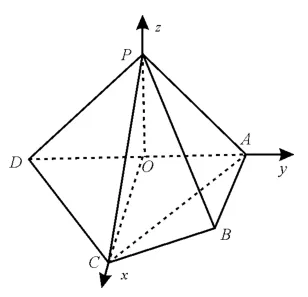
图12
解析:(1)因为平面PAD⊥平面ABCD,AB⊥AD,AB⊂平面ABCD,平面ABCD∩平面PAD=AD,所以AB⊥平面PAD。PD⊂平面PAD,故AB⊥PD。又因为PA⊥PD,PA∩AB=A,所以PD⊥平面PAB。
(2)取AD的中点O,连接PO,CO。因为PA=PD,所以PO⊥AD。又因为PO⊂平面PAD,平面PAD⊥平面ABCD,所以PO⊥平面ABCD。因为CO⊂平面ABCD,所以PO⊥CO。因为AC=CD,所以CO⊥AD。如图12建立空间直角坐标系O-xyz,由题意得A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1)。设平面PCD的法向量为n=(x,y,z),则:

所以在棱PA上存在点M,使得BM∥平面PCD,此时
评注:存在判断型问题的求解,应先假设存在,把问题转化为点的坐标是否有解,借助空间向量列出满足条件的等式求解。运用向量法解题,可使几何问题代数化,降低思维难度。另外,探索在线段AP上(不含端点)是否存在某点M时,要注意三点共线的条件,可由此设出点M的坐标,其中λ为参数,且0<λ<1。
通过以上解答可以看出,利用向量法解题,就是把已知条件和待求量用向量表示,将几何的位置关系的证明或数量关系的运算问题转化为典型向量运算,以算代证,以值定形,减少复杂的空间结构分析,避开抽象、复杂的寻找角的过程,使得思路简捷、方法清晰、运算直接,因此空间向量在解决立体几何问题时扮演着重要的角色,成为处理高考问题的强有力的工具。

