全国名校导数测试卷(A卷)答案与提示
一、选择题
1.B 2.B 3.B 4.D 5.A 6.B 7.B 8.B 9.C 10.D 11.D 12.C 13.C 14.B 15.A 16.D 17.A 18.C 19.B 20.C 21.B 22.B 23.D 24.B 25.B 26.D 27.C 28.A 29.A 30.A 31.A 32.D 33.B 34.B 35.B 36.D
二、填空题
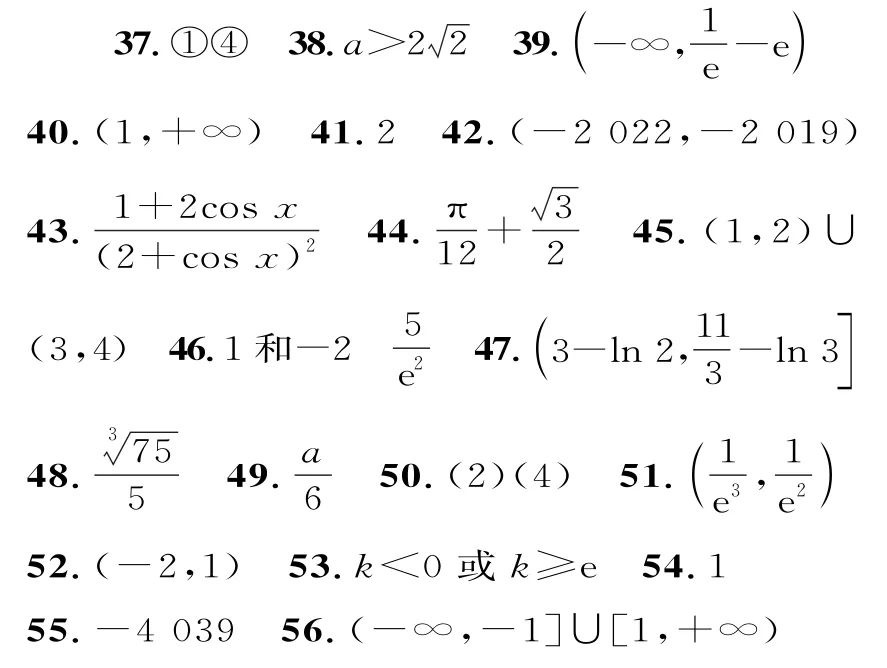
三、解答题
57.(1)g(x)的定义域为,且令h(x)=3+2xlnx,则h'(x)=2(1+lnx)。
(2)由题意知f'(x)=1+lnx-a+2a(x-1)=1+lnx+2ax-3a。
令k(x)=1+lnx+2ax-3a。
因为a>0,所以k(x)在(0,+∞)上单调递增。
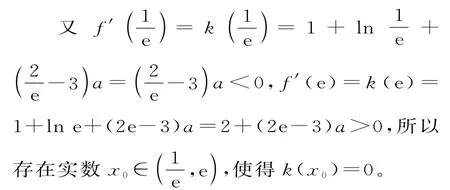
在(0,x0)上,f'(x)<0,f(x)是减函数;在(x0,+∞)上,f'(x)>0,f(x)是增函数。
所以f(x)的最小值是f(x0),其中x0满足f'(x0)=0,即1+lnx0+2ax0-3a=0。
因此,f(x0)=x0lnx0-ax0+1+a(x0-1)2=x0(3a-1-2ax0)-ax0+1+a(x0-1)2=(1-x0)(a+ax0+1)。
①当x0=1,即a=1时,f(x)的最小值为0,此时f(x)有一个零点。
由g(x)的单调性,可得0<a<1。
③当1<x0<e时,f(x0)<0,f(x)有两个零点。
又a>0,所以
由g(x)的单调性,可得a>1。
综上所述,当0<a<1 时,f(x)没有零点;当a=1时,f(x)只有一个零点;当a>1时,f(x)有两个零点。
58.(1)当f(x)≤0 时,由ax-1-xlnx≤0,得
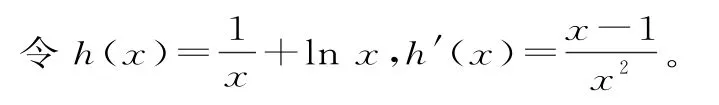
当h'(x)>0时,x>1;当h'(x)<0时,0<x<1。
故h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,h(x)min=h(1)=1。
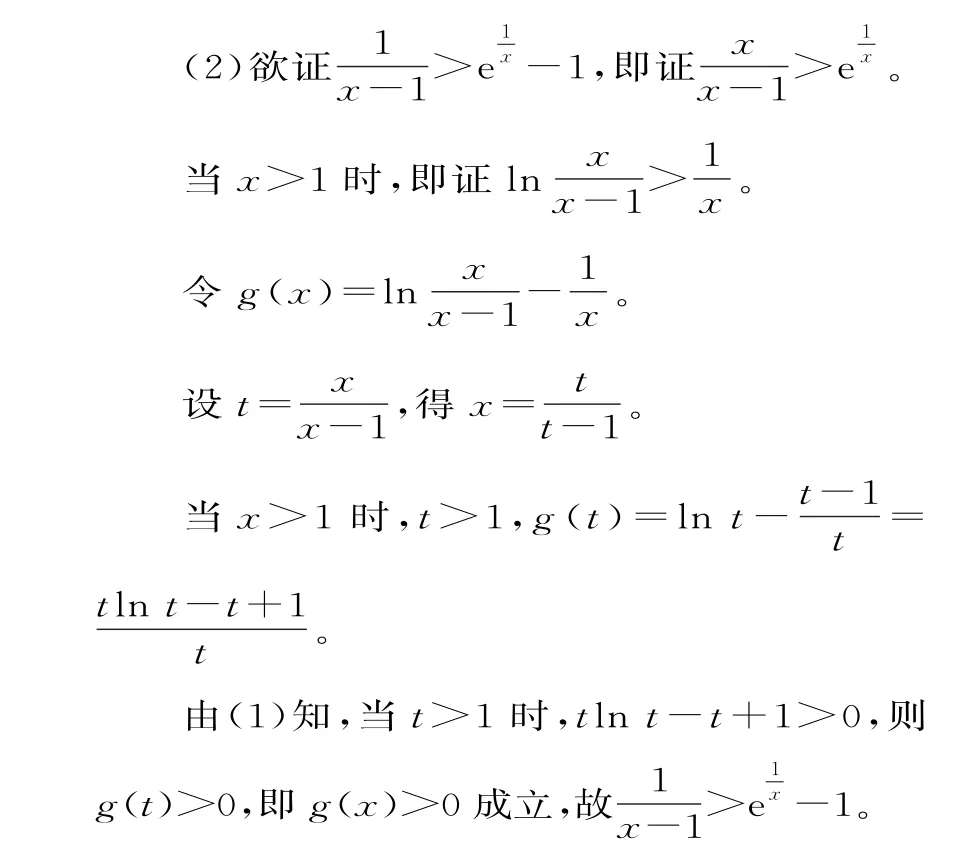
故a≤1。59.(1)由题得f(x)的定义域为(0,+∞)。

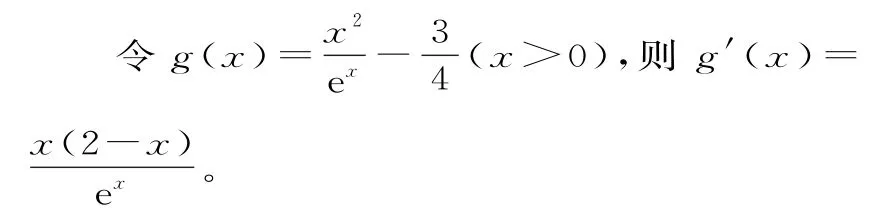
当x∈(0,2)时g'(x)>0,g(x)单调递增;
当x∈(2,+∞)时,g'(x)<0,g(x)单调递减。

令f'(x)>0,即1-lnx>0,解得0<x<e;
令f'(x)<0,即1-lnx<0,解得x>e。
故f(x)在(0,e)上单调递增,在(e,+∞)单调递减。
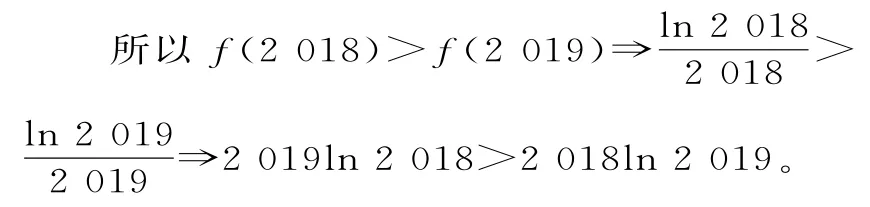
则2 0182019>2 0192018。
(2)不妨设x2>x1>0,由条件知g(x2)=g(x1)=0⇒lnx2-kx2=lnx1-kx1=0。
整理得lnx1+lnx2=k(x1+x2),lnx1-lnx2=k(x1-x2)。
要证x1·x2>e2,只需要证lnx1+lnx2>2,也即证k(x1+x2)>2。
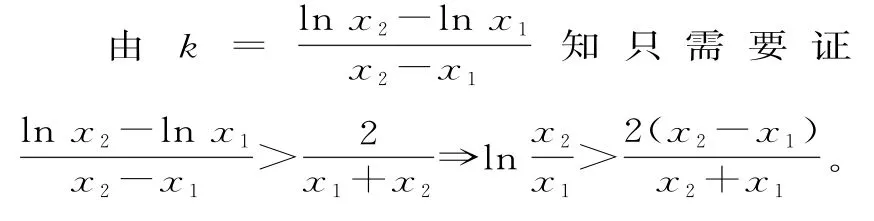

当x∈(-1,0)时,h'(x)>0,h(x)单调递增;当x∈(0,+∞)时,h'(x)<0,h(x)单调递减。所以h(x)max=h(0)=0。
故h(x)≤h(x)max=0,即f(x)≤g(x)。
(2)由(1)可知ln(x+1)≤x对任意的x∈(-1,+∞)恒成立。
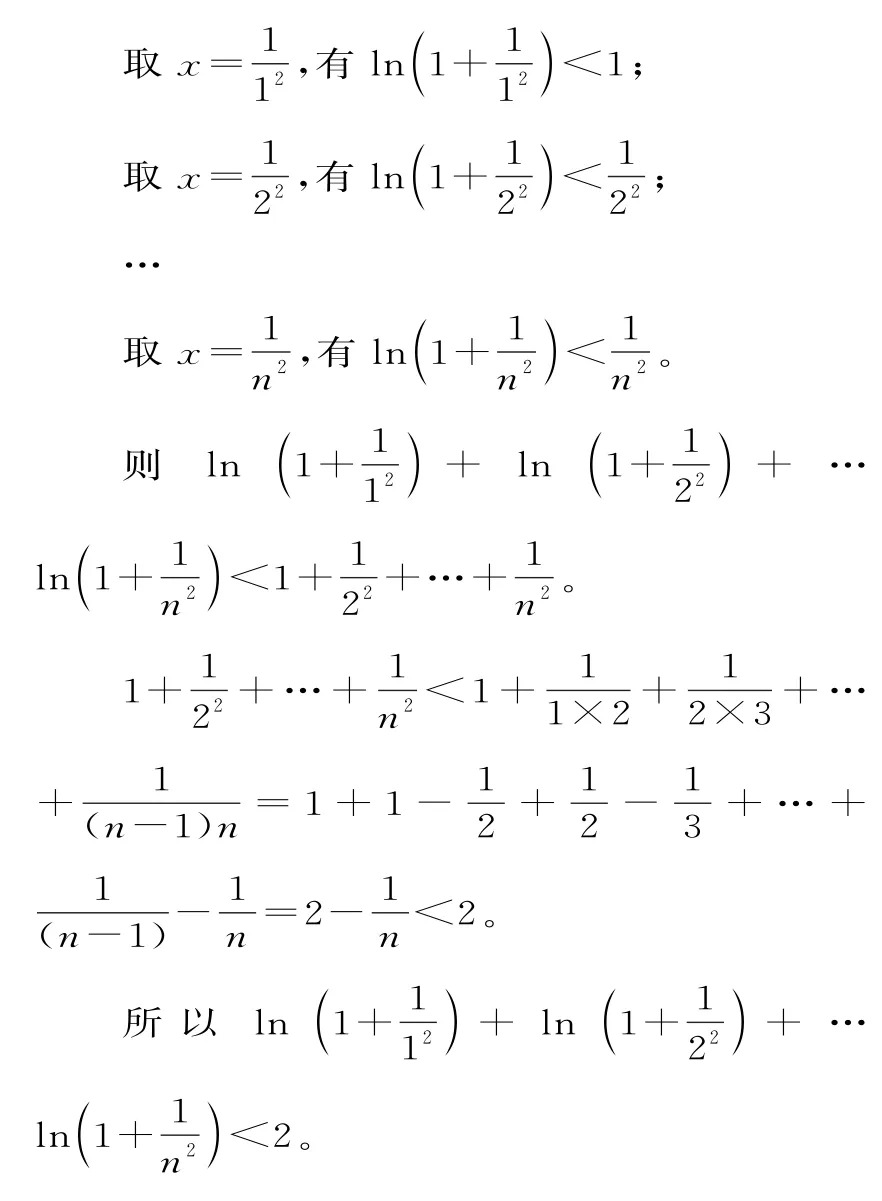

62.(1)由题知f'(x)=-e1-x(-a+cosx)-e1-xsinx=-e1-x(sinx+cosx-a)。
因为函数y=f(x)在[0,π]内存在单调递增区间,所以在区间[0,π]内存在区间使得f'(x)=-e1-x(sinx+cosx-a)>0成立。
也即sinx+cosx-a<0能成立。

要证原不等式成立,只要证ex+2-2e1-x·(sinx+cosx)>0,也即证:
ex+2>2e1-x(sinx+cosx)。


63.(1)由f(x)=x2(6lnx-4x+6a-3),x∈(0,+∞),得f'(x)=12x(lnx-x+a)。
函数f(x)有两个极值点等价于f'(x)=0在(0,+∞)上有两个不同零点,等价于lnx-x+a=0在(0,+∞)上有两个不同根。
令g(x)=lnx-x+a,则
当x∈(0,1)时,g'(x)>0,g(x)单调递增;
当x∈(1,+∞)时,g'(x)<0,g(x)单调递减。
所以g(x)max=g(1)=a-1。
当a≤1 时,g(x)≤0 恒成立,f(x)在(0,+∞)上单调递减,不可能有两个极值点,应舍去。
当a>1时,e-a∈(0,1),ea∈(1,+∞),g(e-a)=-e-a<0,g(ea)=2a-ea<0,g(1)>0。
由零点存在性定理得g(x)在(0,1)和(1,+∞)内分别存在一个变号零点,此时f(x)有两个极值点。
综上,所求a的取值范围为(1,+∞)。
(2)因为x1,x2(x1<x2)是f(x)的两个极值点,所以a>1,且g(x1)=g(x2)。
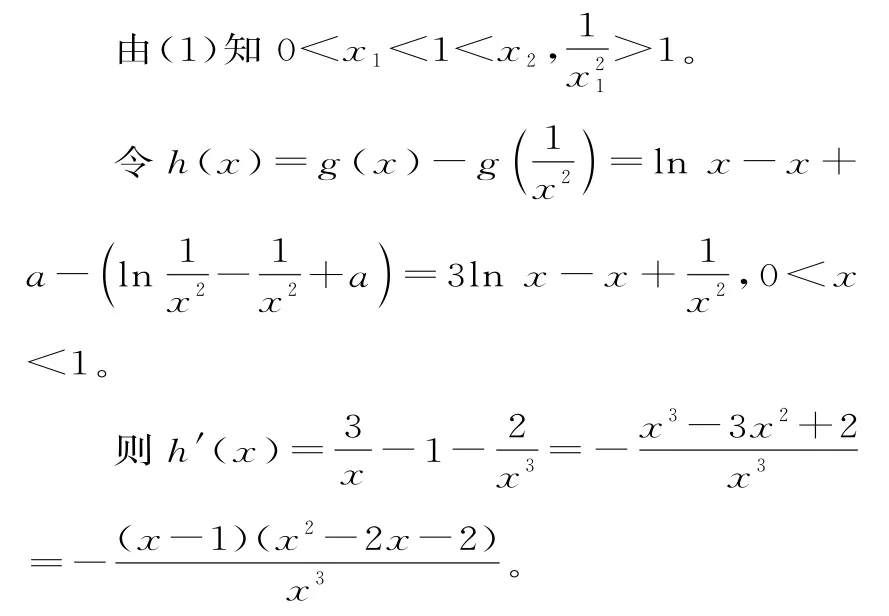
由x2-2x-2<0 在0<x<1 恒成立,得0<x<1时,h'(x)<0,h(x)单调递减。
又h(1)=0,所以0<x<1 时,h(x)>0,即


