浅谈向量在求角问题中的应用

■重庆市铁路中学校

立体几何中涉及的角很多,线线角、线面角、面面角等,它是立体几何中的一个难点。若用向量的方法解决此类问题,则解题思路简捷。本文就向量在求角问题中常用的一些方法举例说明,供同学们参考。

一、求异面直线所成角(0°＜θ≤90°)

设a,b分别为异面直线a,b的方向向量,利用两向量夹角的余弦公式：

例1如图1,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=,求异面直线BF与DE所成的角的大小。

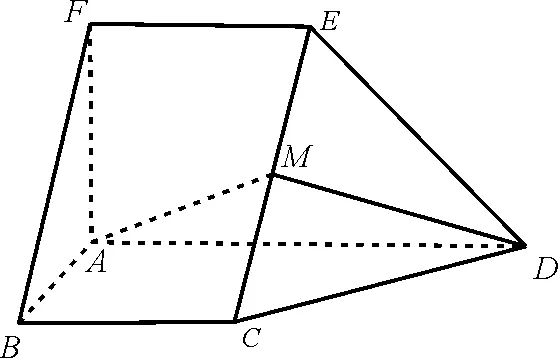
图1

解析：如图2 所示,建立空间直角坐标系,点A为坐标原点。

图2

所以异面直线BF与DE所成的角的大小为60°。

点评：如果用传统的立体几何方法求BF与DE所成角的余弦值,需用平移的方法来找线线角,解三角形则是非常复杂的,而像这样采用向量的方法求解则显得比较新颖直观。

练习：在四棱锥P-ABCD中,底面AB-CD为矩形,侧棱PA⊥底面ABCD,AB=,E为PD的中点,求直线AC与PB所成角的余弦值。

所以AC与PB所成角的余弦值为

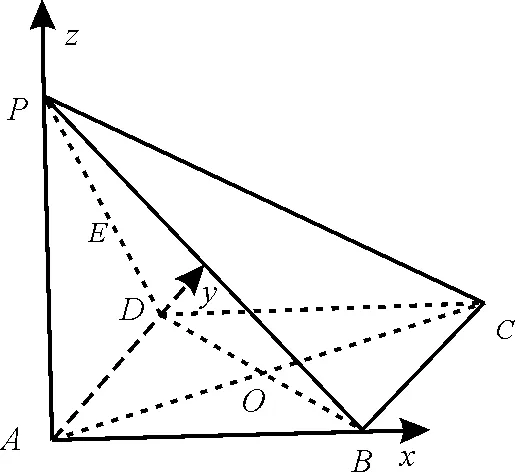
图3

二、求直线与平面所成角(0°≤θ≤90°)

设a是直线l的方向向量,n是平面α的法向量,直线l与平面α所成的角为θ,则

例2如图4,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC。

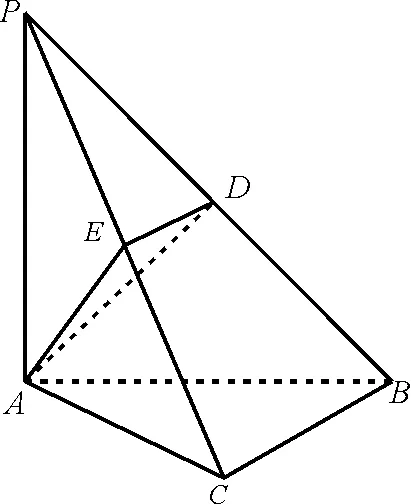
图4

(1)求证：BC⊥平面PAC;

(2)当D为PB的中点时,求AD与平面PAC所成角的余弦值。

解析：如图5,以A为原点建立空间直角坐标系A-xyz。

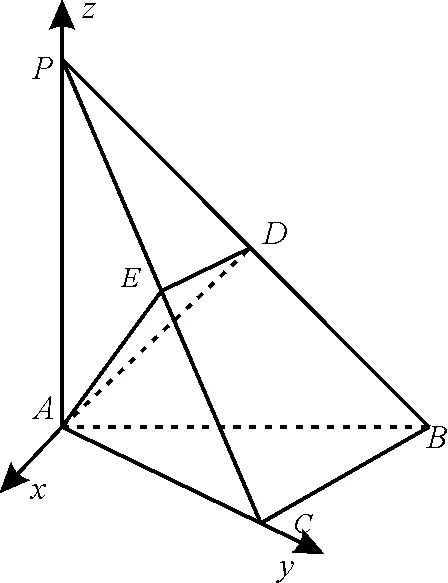
图5

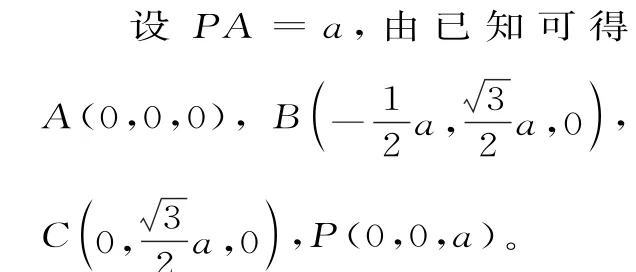
(1)因为,所以

又因为∠BCA=90°,所以BC⊥AC。

因此,BC⊥平面PAC。

(2)因为D为PB的中点,DE∥BC,所以E为PC的中点。

又由(1)知,BC⊥平面PAC,则DE⊥平面PAC,垂足为点E。

∠DAE是AD与平面PAC所成的角。

故AD与平面PAC所成角的余弦值为

点评：建立空间坐标系研究空间图形,宜从实际图形出发,合理选好坐标轴,可使点、线的表示简化,运算简明快捷。选坐标轴可充分利用所讨论的空间图形的已有直线的关系和性质,如垂直关系或对称性质等等。

练习：已知正方体ABCD-A1B1C1D1中,E是CC1的中点,求BE与平面BB1D所成的角的余弦值。

解析：如图6,建立空间直角坐标系,并设正方体的棱长为2, 则D(0,0,0),B(2,2,0,),B1(2,2,2),E(0,2,1)。

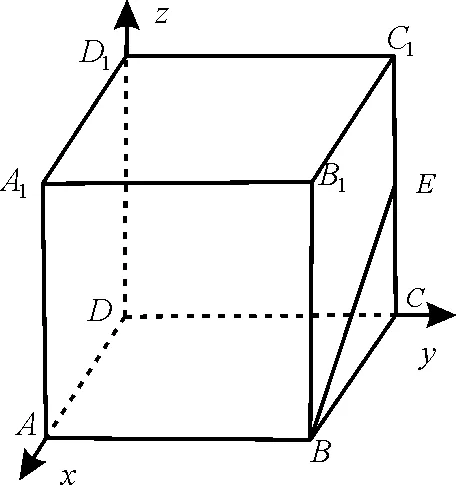
图6

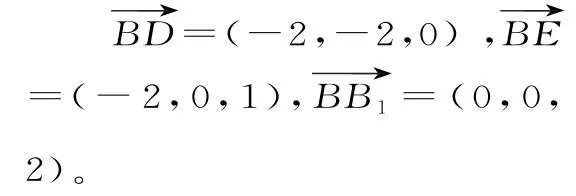
设y=1,则n=(―1,1,0)。

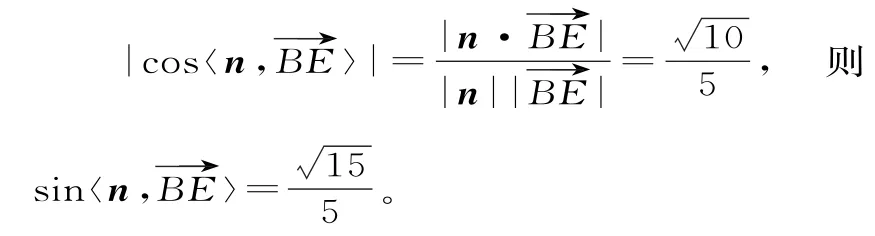
故BE与平面BB1D所成的角的余弦值为

练习：正三棱柱ABC-A1B1C1的底面边长是a,侧棱长是, 求AC1与侧面ABB1A1所成的角。

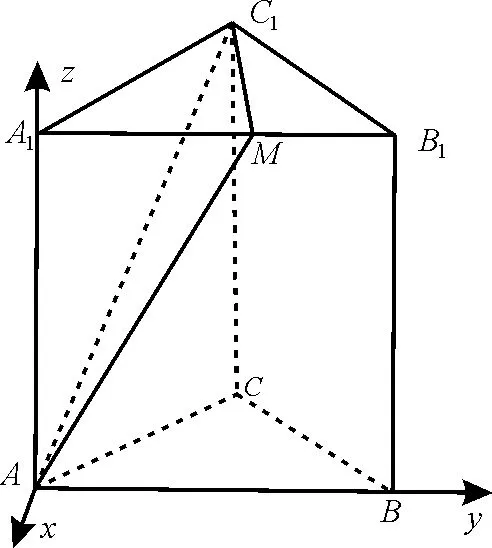
图7

三、求两个平面的二面角(0°≤θ≤180°)

在平面角为θ的二面角α-a-β中,m,n分别为α,β的法向量,则θ与相等或互补,

例3如图8,在直四棱柱A1B1C1D1-ABCD中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点。

图8

(1)证明：直线EE1∥平面FCC1;

(2)求二面角B-FC1-C的余弦值。

解析：(1)因为AB=4,BC=CD=2,F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形。 因为ABCD为等腰梯形,所以∠BAC=∠ABC=60°。取AF的中点M,连接DM,则DM⊥AB,所以DM⊥CD。

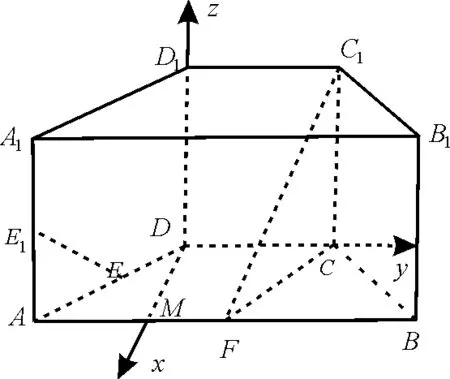
图9

点评：用向量法求二面角的大小,首先求出两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小。

练习：如图10,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD。

(1)证明：AB⊥平面VAD;

(2)求二面角V-AD-B的余弦值。

解析：(1)因为平面VAD⊥底面ABCD,平面VADB平面ABCD=AD,且AB⊥AD,ABC平面ABCD,所以AB⊥平面VAD。作AD的中点O,则VO⊥底面ABCD。建立如图10 空间直角坐标系,并设正方形边长为1,则

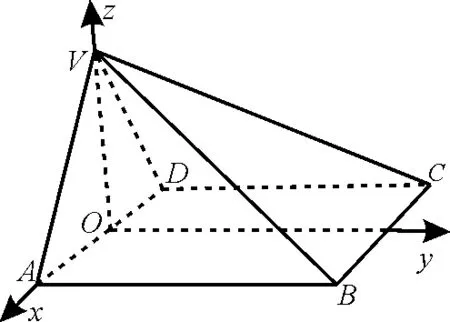
图10

小结：通过用向量的方法处理立体几何中有关角的问题,我们可以看出它确实比用传统的几何方法解决问题有许多优越性。因此,我们应该熟练灵活地应用向量这一工具,快而准地解决立体几何中有关角的问题。