例谈导数中双变量问题的常见处理策略

■河北省南宫中学

双变量问题,一直都是各地高考及模拟考试的热点问题,试题常常出现在试卷的“压轴”位置。这类问题综合性强,难度大,对同学们的数学素养要求很高,因此具有很好的区分度。同学们一旦遇到此类问题,处理起来往往是顾此失彼,难以入手。正是基于这点,下面例谈导数中双变量问题的常见解题策略。

策略一 相互替代法

当出现双变量问题时,若能将双变量中所有变量统一用其中一个变量来替换,这样就将双变量问题转化为我们熟知的单变量问题,从而为我们的解题带来便利。

例1(2018年全国Ⅰ卷理科第21题)已知函数

(1)讨论函数f(x)的单调性;

(2)若f(x)存在两个极值点x1,x2,证明

解析：(1)当a≤2 时,f(x)的递减区间为(0,+∞),无递增区间;

当a＞2 时,f(x)的递减区间为递增区间为(解题过程略)

所以x1x2=1,x1+x2=a(由(1)知a＞2),即

不妨设x1＜x2,则0＜x1＜1＜x2。

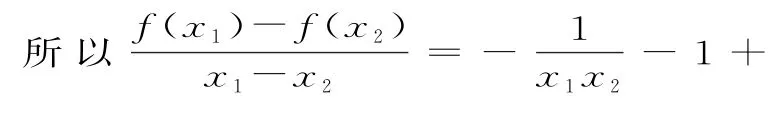
评析：本题中利用x1x2=1 将双变量问题转化为关于x2的单变量问题(实际上转化为关于x1的单变量问题亦可),从而借助函数单调性得以将问题解决。

策略二 主元法

当问题中含有的变量较多且变量之间互不影响时,可以选择一个量作为主元,并以此为线索来解决问题,这样的方法叫作主元法。有些问题,巧妙设置主元,可以使问题化繁为简,事半功倍,给以一种耳目一新的感觉。

例2(2018 年全国Ⅰ卷文科第21 题改编)已知函数f(x)=aex-lnx-1。

故g(x)min=g(1)=0,g(x)≥0,即ex-1-lnx-1≥0,命题得证。

评析：对于含有参数的函数不等式证明问题,常见的处理策略就是先将参数消掉,进而转化为单变量问题来处理。本题中先将f(x)视为关于参数a的一次函数,利用函数的单调性将参数消掉,进而转化为关于x的单变量问题来处理。

策略三 引入变量法

当题目中的变量之间的关系比较隐蔽或无法相互替换时,可以考虑引入新的变量,用新的变量来表示其他变量,达到减少变量的目的。

例3(2018年山西太原高三下学期第二次模拟考试理科第12 题)已知函数f(x),若g(m)=f(n)成立,则n-m的最小值为( )。

评析：本题中直接寻求变量m、n之间的关系不易发现,但是通过引入“中间变量t”,将m、n分别视为t的函数,从而顺利实现消元的目的。

策略四 整体代换法

有些题目可以通过整体代换突破双变量的困扰,将双量问题化为单变量问题。常见的整体代换有比值代换、差值代换、乘积代换三种。

例4(比值代换)∀a＞0,b＞0且a≠b,证明：(对数均值不等式)。

证明：由对称性,不妨设a＞b＞0。

综上,结论得证。

例5(差值代换)已知曲线C：f(x)=ex,直线l：g(x)=k(x-1)(k＞0),直线l与曲线C交于A、B两点,其横坐标分别为x1、x2,令x1＜x2,求证：x1x2＜x1+x2。

解析：由题意可得,ex1=k(x1-1),ex2=k(x2-1),则

例6(乘积代换)(2018年浙江卷第22题)已知函数

若f(x)在x=x1,x=x2(x1≠x2)处导数相等,证明：f(x1)+f(x2)＞8-8ln 2。

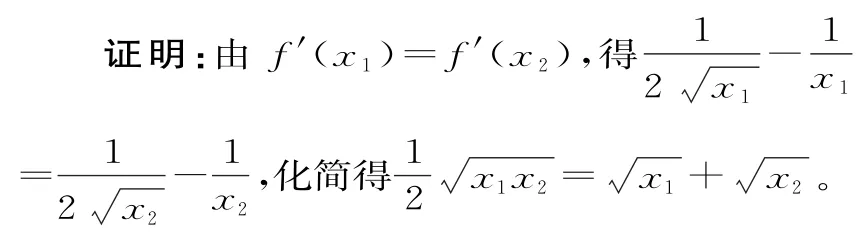
故f(x1)+f(x2)＞8-8ln 2。

评析：整体代换中以“比值代换”和“差值代换”最为常见,但是无论那种代换都需要灵活的代数变形,从而通过整体代换的策略,转换为单变量问题。