构造新函数 妙解导数题

■广东省汕头市澄海凤翔中学

导数是高考函数内容的重要组成部分,导数既是数学研究的对象,也是研究数学的工具,在解决导数与抽象函数、不等式相结合的有关问题时,观察条件结构、构造函数是解决问题的关键。

一、含有ex 的函数

例1设函数f(x)的导函数为f'(x),对任意x∈R 都有f(x)＞f'(x)成立,则( )。

A.3f(ln 2)＞2f(ln 3)

B.3f(ln 2)=2f(ln 3)

C.3f(ln 2)＜2f(ln 3)

D.3f(ln 2)与2f(ln 3)的大小不确定

故选A。

点评：若f'(x)-kf(x)＞0,则构造函数,其中当k=1时,则构造函数

例2已知定义在R 上的函数f(x)的导函数为f'(x),对任意x∈R 满足f(x)+f'(x)＜0,则下列结论正确的是( )。

A.2f(ln 2)＞3f(ln 3)

B.2f(ln 2)＜3f(ln 3)

C.2f(ln 2)≥3f(ln 3)

D.2f(ln 2)≤3f(ln 3)

解析：设g(x)=exf(x),则g'(x)=(ex)'f(x)+exf'(x)=ex[f(x)+f'(x)]＜0,g(x)在R 上是减函数。因为ln 2＜ln 3,所以g(ln 2)＞g(ln 3),即(ln 2)＞eln3f(ln 3), 2f(ln 2)＞3f(ln 3)。

故选A。

点评：若f'(x)+kf(x)＞0,则构造函数F(x)=ekxf(x),其中当k=1时,则构造函数F(x)=exf(x)。

二、含有xn 的函数

例3已知函数若对任意的x∈[1 ,2],xf'(x)+f(x)＞0恒成立,则实数t的取值范围是( )。

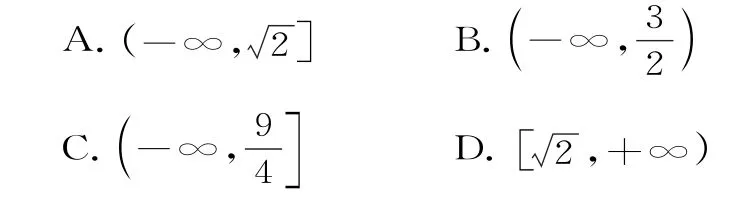
点评：若xf'(x)+nf(x)＞0,则构造函数F(x)=xnf(x),其中当n=1时,则构造函数F(x)=xf(x)。

三、含有sin x 的函数

例5函数f(x)的定义域是f'(x)是它的导函数,且f(x)+tanx·f'(x)＞0在定义域内恒成立,则( )。

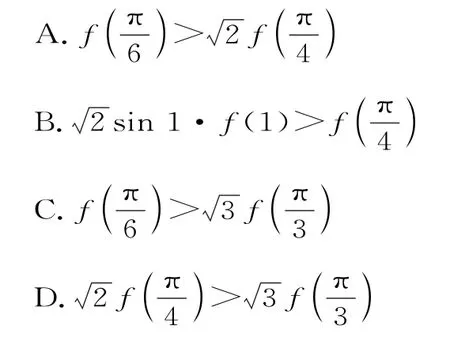
解析：设g(x)=sinx·f(x),则：

g'(x)=cosx·f(x)+sinx·f'(x)=cosx[f(x)+tanx·f'(x)]＞0。

故选B。

点评：若f(x)+f'(x)tanx＞0 或f(x)cosx+f'(x)sinx＞0,则构造函数F(x)=sinx·f(x)。

例6已知定义在上的函数f(x)的导函数为f'(x),且对于任意的x∈,都有f'(x)sinx＜f(x)cosx,则下列结论正确的是( )。

点评：若f(x)-f'(x)tanx＞0 或f(x)cosx-f'(x)sinx＞0,则构造函数

四、含有cos x 的函数

例7设函数f'(x)是定义在(0,2π)上的函数f(x)的导函数,f(x)=f(2πx)。当0＜x＜π 时,f(x)sinx-f'(x)·cosx＜0,若,则( )。

A.a＜b＜cB.b＜c＜a

C.c＜b＜aD.c＜a＜b

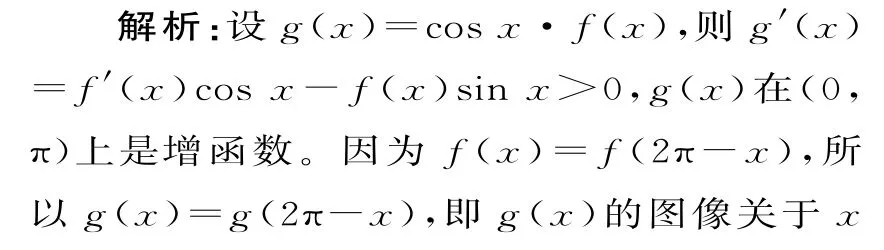
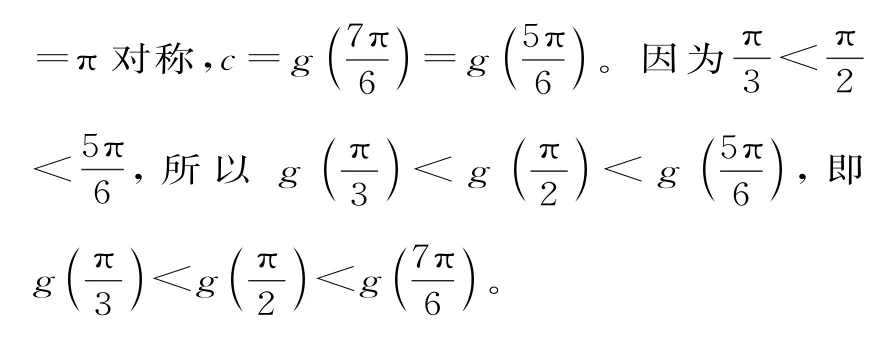
则a＜b＜c,选A。

点评：若f'(x)-f(x)tanx＞0 或f'(x)cosx-f(x)sinx＞0,则构造函数F(x)=cosx·f(x)。

例8已知函数y=f(x)对于任意的满足f'(x)cosx+f(x)sinx=1+lnx(其中f'(x)是函数f(x)的导函数),则下列不等式成立的是( )。

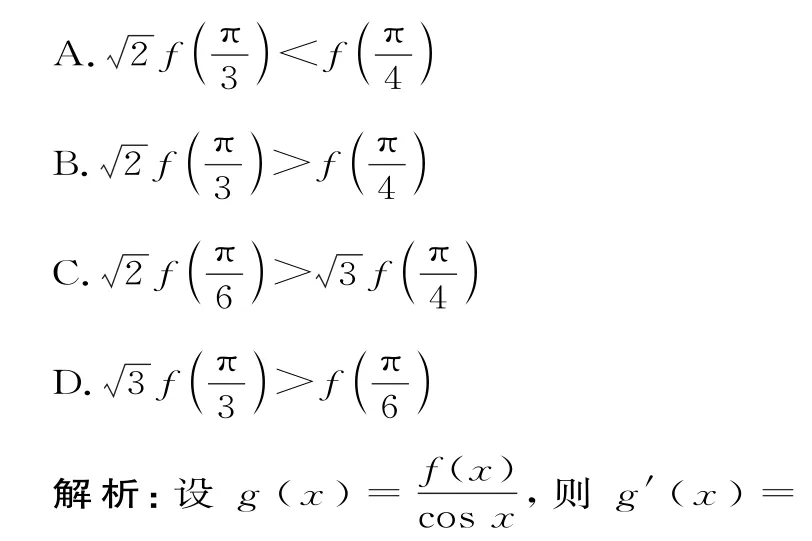
整理可知,选B。

点评：若f'(x)+f(x)tanx＞0 或f'(x)cosx+f(x)sinx＞0,则构造函数