聚焦2019 年高考导数经典问题

■陕西洋县中学 (特级教师)

2019年高考导数主要围绕“利用导数求曲线的切线、 确定单调区间 、求极值和最值、求参数范围以及用导数研究函数零点和解决与函数有关的不等式”等经典问题展开,彰显导数的工具性和应用性。

聚焦1 利用导数的几何意义探求曲线的切线方程

例1(2019年江苏卷第11题)在平面直角坐标系xOy中,点A在曲线y=lnx上,且该曲线在点A处的切线经过点(-e,-1)(e为自然对数的底数),则点A的坐标是_____。

解析：设出切点坐标,得到切线方程,然后求解方程得到横坐标的值,可得切点坐标。

设点A(x0,y0),则y0=lnx0。

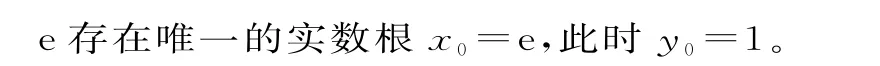
故点A的坐标为A(e,1)。

品味：利用导数工具研究曲线的切线方程,渗透了直观想象、逻辑推理和数学运算等素养。解超越方程,一般是构造函数,导数法求解函数的零点,凸显导数的工具性和可操作性。

变式1(1)(2019年全国Ⅲ卷文数第7题)已知曲线y=aex+xlnx在点(1,ae)处的切线方程为y=2x+b,则( )。

A.a=e,b=-1

B.a=e,b=1

C.a=e-1,b=1

D.a=e-1,b=-1

(2)(2019全国Ⅱ卷文数第10题)曲线y=2sinx+cosx在点(π,-1)处的切线方程为( )。

A.x-y-π-1=0

B.2x-y-2π-1=0

C.2x+y-2π+1=0

D.x+y-π+1=0

解析：(1)y=aex+xlnx的导数为y'=aex+lnx+1。

由函数y=aex+xlnx在点(1,ae)处的切线方程为y=2x+b,可得ae+0+1=2,解得a=e-1。又切点为(1,1),可得1=2+b,即b=-1。故选D。

(2)当x=π时,y=2sin π+cos π=-1,故点(π,-1)在曲线y=2sinx+cosx上。因为y'=2cosx-sinx,所以y'|x=π=2cos π-sin π=-2,则y=2sinx+cosx在点(π,-1)处的切线方程为y-(-1)=-2(x-π),即2x+y-2π+1=0。故选C。

聚焦2 利用导数的几何意义探究最值和曲线的公切线

例2(2019 年高考江苏卷第10 题)在平面直角坐标系xOy中,P是曲线y=x)上的一个动点,则点P到直线x+y=0的距离的最小值是____。

品味：曲线上任意一点到已知直线的最小距离,形助数转化为曲线上过切点的切线与已知直线平行的平行线之间的距离。借助导数的几何意义确定切点坐标,利用点到直线的距离公式求解,渗透了直观想象和数学运算素养,凸显数形结合和转化与化归思想在解题中的应用。

变式2(2019年全国Ⅱ卷理数第20题节选)已知函数,设x0是f(x)的一个零点,证明：曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线。

设曲线y=ex的切点为B(x1,ex1),在切点为B(x1,ex1)处的切线l'。因为y=ex,所以y'=ex,在B(x1,ex1)处的切线l'的斜率为ex1,切线l'的方程为y=ex1x+ex1(1-x1)。

当切线l'的斜率k1=ex1等于直线l的斜率时,即

切线l'在纵轴的截距为当直线l,l'的斜率相等时,在纵轴上的截距也相等,因此直线l,l'重合,则曲线y=lnx在A(x0,lnx0)处的切线也是曲线y=ex的切线。

聚焦3 利用导数研究函数的单调性求解函数不等式恒成立

例3(2019 年天津理数第8 题)已知a∈R, 设函数f(x) =若关于x的不等式f(x)≥0在R 上恒成立,则a的取值范围为( )。

A.[0,1] B.A

C.[0,e] D.[1,e]

解析：此题为分段函数不等式恒成立问题,可借助分界点对x分类,分离参数转化为新函数的值域求解。当x=1时,f(1)=1-2a+2a=1＞0,显然恒成立。

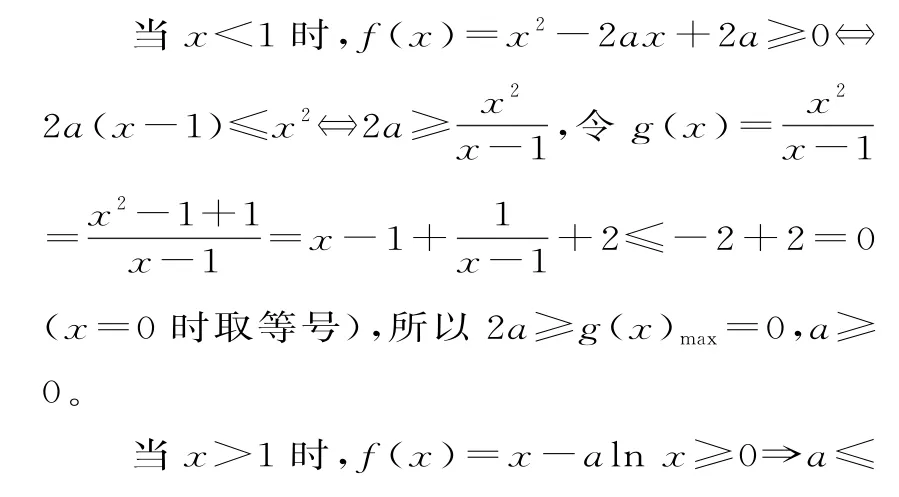
当x＞e时,h'(x)＞0,h(x)递增;当1＜x＜e时,h'(x)＜0,h(x)递减。

当x=e时,h(x)取得最小值h(e)=e,因此,a≤h(x)min=e。

综上,a的取值范围是[0,e]。

品味：函数不等式区间上恒成立,合理分离参数,a≤f(x)在D上恒成立,等价于a≤f(x)min,x∈D;a≥f(x)在D上恒成立,等价于a≥f(x)max,x∈D。构造新函数用不等式或导数法研究单调性求解。

变式3(2019 年内蒙古鄂尔多斯市5月模拟卷)设f(x)=ex-e-x-x。

(1)求f(x)的单调区间;

(2)已知g(x)=x2f(x)+(x+1)·[f(x)+(1-a)x]+(1-a)x3,若对所有x≥0,g(x)≥0恒成立,求实数a的取值范围。

解析：(1)由f(x)=ex-e-x-x,得f'(x)=ex+e-x-1≥1＞0,则f(x)在(-∞,∞)上是增函数,单调增区间为(-∞,+∞)。

(2)化简得g(x)=(x2+x+1)f(x)+(1-a)x(x+1)+(1-a)x3=(x2+x+1)·[f(x)+(1-a)x]。

显然x2+x+1＞0,故若使g(x)≥0,只需f(x)+x(1-a)=ex-e-x-ax≥0即可。

令h(x)=ex-e-x-ax,则h'(x)=ex+e-x-a≥2-a。

①当2-a≥0,即a≤2时,h'(x)≥0恒成立,h(x)在[0,+∞)上为增函数。

故h(x)≥h(0)=0,即g(x)≥0 在[0,+∞)上恒成立。

②当a＞2时,令h'(x)=0,即ex+e-x-a=0,可化为(ex)2-aex+1=0。

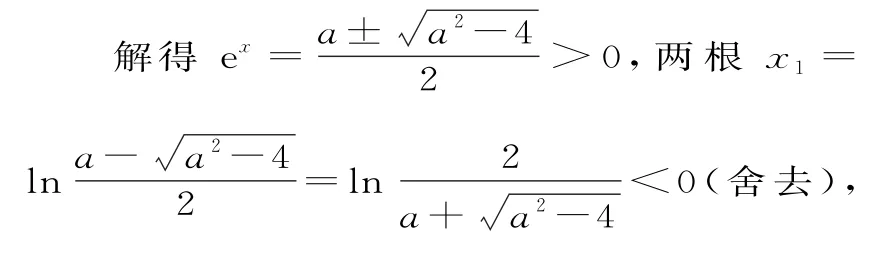
当0＜x＜x2时,,h'(x)＜0,h(x)在[0,x2]上为减函数。

又h(0)=0,h(x2)＜0。

故当a＞2 时,h(x)≥0 不恒成立,即g(x)≥0不恒成立。

综上所述,a的取值范围为(-∞,2]。

聚焦4 利用导数研究函数的单调性进而确定最值

例4(2019年全国Ⅲ卷理数第20题)已知函数f(x)=2x3-ax2+b。

(1)讨论f(x)的单调性。

(2)是否存在a,b,使得f(x)在区间[0,1]最小值为-1且最大值为1? 若存在,求出a,b的所有值;若不存在,说明理由。

解析：(1) 求f(x)的导数, 根据a的范围分情况讨论导函数值的正负,确定函数单调性, 对f(x)=2x3-ax2+b,求导得

(2) 根据a的各种范围,利用函数单调性进行最大值和最小值的判断,最终求出a,b的值。

(i) 当a≤0时,由(1)知,f(x)在[0,1]上单调递增,所以f(x)在区间[0,1]的最小值为f(0)=b,最大值为f(1)=2-a+b。此时a,b满足题设条件当且仅当b=-1,2-a+b=1,即a=0,b=-1。

(ii)当a≥3时,由(1)知,f(x)在[0,1]上单调递减,所以f(x)在区间[0,1]的最大值为f(0)=b,最小值为f(1)=2-a+b。此时a,b满足题设条件当且仅当2-a+b=-1,b=1,即a=4,b=1。

(iii)当0＜a＜3 时,由(1)知,f(x)在[0,1]上的最小值为,最大值为b或2-a+b。

综上,当且仅当a=0,b=-1 或a=4,b=1时,f(x)在[0,1]的最小值为-1,最大值为1。

品味：求函数单调区间,常常是求出函数的导函数且化因式为积,借助导函数零点分类探究导函数值在各个区间的正负,进而确定单调区间,导函数零点的大小是分类的依据,函数区间上的最大值最小值,借助所给区间和所求出的单调区间的关系,合理分类探究。

变式4(2018年江苏卷)若函数f(x)=2x3-ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[-1,1]上的最大值与最小值的和为____。

解析：结合三次函数图像确定在(0,+∞)上有且仅有一个零点的条件,求出参数a,再根据单调性确定函数最值。已知f'(x)因为函数f(x)在(0,+∞)上有且仅有一个零点,且f(0)=1,所以=0,则a=3。则f(x)在[-1,0]上单调递增,在[0,1]上单调递减,所以f(x)max=

故f(x)max+f(x)min=f(0)+f(-1)=1-4=-3。

聚焦5 利用导数研究函数极值和函数的零点问题

例5(2019年全国Ⅰ卷理数第20题)已知函数f(x)=sinx-ln(1+x),f'(x)为f(x)的导数。证明：(1)f'(x)在区间内存在唯一极大值点;(2)f(x)有且仅有2个零点。

解析：(1)求导判断导函数在上单调递减,借助零点存在定理判断推证。

① 当x∈(-1,0]时,由(1)可知f'(x)在(-1,0]上单调递增,故f'(x)≤f'(0)=0,f(x)在(-1,0]上单调递减。

若f(x)=0,则x=0,f(x)在(-1,0]上的唯一零点。

又f'(0)=0 , 则f'(x0)＞0,f(x)在(0,x0)上单调递增,此时f(x)＞f(0)=0,不存在零点。

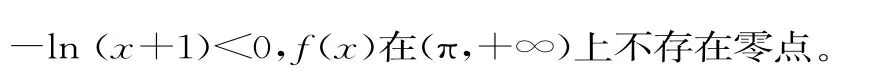
综上所述,f(x)有且仅有2个零点。

品味：本题考查导数与函数极值之间的关系,利用导数解决函数零点个数的问题。函数y=f(x)在x=x0处取极值的充要条件为：(1)f'(x0)=0;(2)在x=x0左右两侧的导数值的符号相反。解决零点问题的关键：一方面是利用零点存在定理或最值点来说明存在零点,另一方面是利用函数的单调性说明在区间内零点的唯一性,二者缺一不可。

变式5(2019 全国Ⅱ卷文数第21 题)已知函数f(x)=(x-1)lnx-x-1。证明：

(1)f(x)存在唯一的极值点;

(2)f(x)=0有且仅有两个实根,且两个实根互为倒数。

解析：(1)易求f(x)的定义域为(0,

因为y=lnx单调递增,单调递减,所以f'(x)单调递增。又f'(1)=-1＜,故存在唯一x0∈(1,2),使得f'(x0)=0。

又当x＜x0时,f'(x)＜0,f(x)单调递减;当x＞x0时,f'(x)＞0,f(x)单调递增。

因此,f(x)存在唯一的极值点。

(2)由(1)得到f(x)=0在(x0,+∞)内存在唯一实根,记作x=α。

由(1)知f(x0)＜f(1)=-2,且f(e2)=e2-3＞0,所以f(x)=0在(x0,+∞)内存在唯一根x=α。

综上,f(x)=0有且仅有两个实根,且两个实根互为倒数。