如何破解导数中的隐零点问题

■河北省张家口市二中

导数中的隐零点问题多见于通过多次求导,判断导函数的正负,确定原函数的单调区间,从而确定原函数的最值,或者求出参数的取值范围。同学们虽然零点求不出来,但是找到零点满足的方程、满足的关系式,经过变形,代入新构造的函数中,可通过消元、换元以及降次达到解题的目的。

例1设函数f(x)=lnx-x,g(x)=xex-2x-1,证明：当x＞0 时,g(x)≥f(x)。

证明：令F(x)=g(x)-f(x)=xexlnx-x-1(x＞0)。

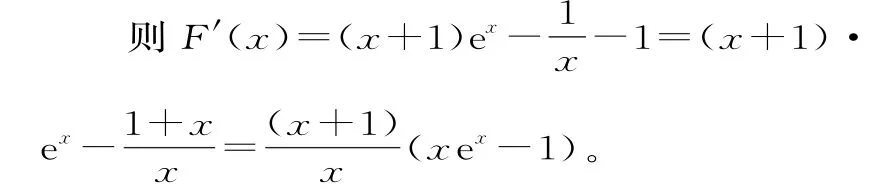
令G(x)=xex-1,则当x＞0时,G'(x)=(x+1)ex＞0,函数G(x)在(0,+∞)上单调递增。因为G(0)=-1,G(1)=e-1＞0,所以G(x)存在唯一的零点c∈(0,1)。且当x∈(0,c)时,G(x)＜0;当x∈(c,+∞)时,G(x)＞0。

故当x∈(0,c)时,F'(x)＜0;当x∈(c,+∞)时,F'(x)＞0。

F(x)在(0,c)上单调递减,在(c,+∞)上单调递增,从而F(x)≥F(c)=cec-

由G(c)=0,得cec-1=0,cec=1。

两边取对数得,lnc+c=0。F(c)=(cec-1)-(lnc+c)=0,F(x)≥F(c)=0,故g(x)≥f(x)。

注意：G(c)=0,cec-1=0的应用。

例2设函数f(x)=xlnx-x2+2-x(a∈R),k∈N,g(x)=2-2x-x2,且当x＞2时不等式k(x-2)+g(x)＜f(x)恒成立,试求k的最大值。

解析：由已知k(x-2)+g(x)＜f(x),可得k(x-2)+2-2x-x2＜xlnx-x2+2-x,也即k(x-2)＜xlnx+x。

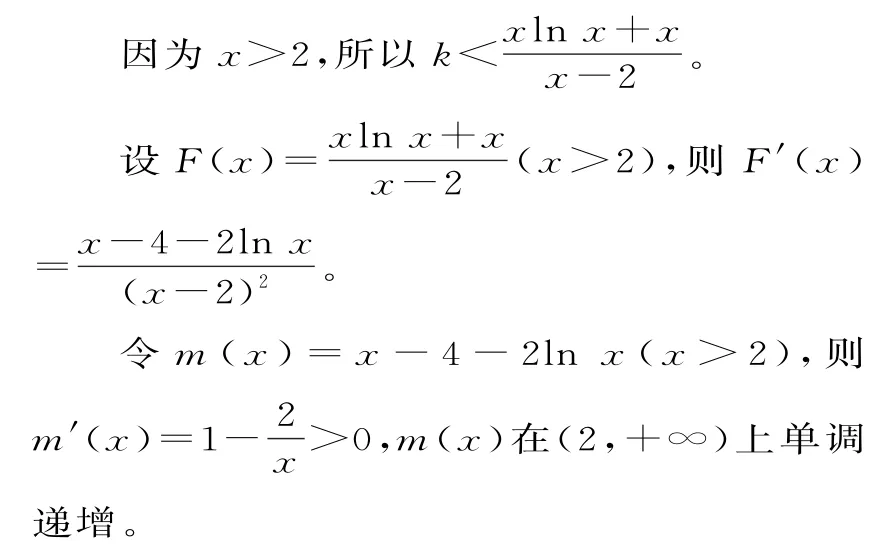
m(8)=4-2ln 8＜4-2ln e2=4-4=0,m(10)=6-2ln 10＞6-2ln e3=6-6=0。

所以函数m(x)在(8,10)上有唯一的零点x0,即x0-4-2lnx0=0。当2＜x＜x0时,m(x)＜0,即F'(x)＜0;当x0＜x时,F'(x)＞0。

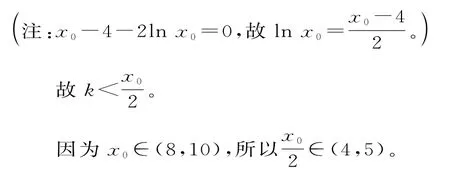
k的最大值为4。

注意：m(x0)=0,即x0-4-2lnx0=0的应用。

例3证明：x＞0,x-xlnx≤e-x+x2。

证明：要证x-xlnx≤e-x+x2,只需证e-x+x2-x+xlnx≥0。

设h(x)=e-x+x2-x+xlnx,x＞0,则h'(x)=-e-x+2x+lnx。

令g(x)=h'(x),则g'(x)=e-x+2+,所以函数h'(x)=-e-x+2x+lnx单调增。

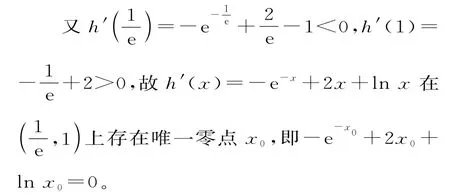
所以当x∈(0,x0)时,h'(x)＜0;当x∈(x0,+∞)时,h'(x)＞0。函数h(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,故

因为1+x0＞0,所以只要x0+lnx0≥0即可。

当x0+lnx0＜0时,lnx0＜-x0⇒x0＜,所以x0+lnx0＜0 与矛盾,故x0+lnx0≥0,得证。

注意：h'(x0)=0,即=0的应用。本题中还应用了反证法来证明不等式x0+lnx0≥0。

例4已知函数f(x)=2ex-(x-a)2+3,a∈R,若x≥0,f(x)≥0 恒成立,求a的取值范围。

解析：f'(x)=2(ex-x+a)。令h(x)=2(ex-x+a)(x≥0),则h'(x)=2(ex-1)≥0。

故h(x)在[0,+∞)上单调递增,且h(0)=2(a+1)。

①当a≥-1 时,f'(x)=h(x)≥0 在[0,+∞)上恒成立,即函数f(x)在[0,+∞)上单调递增。

②当a＜-1 时,则存在x0＞0,使h(x0)=0。当x∈[0,x0)时,h(x)＜0 即f'(x)＜0,则f(x)单调递减;当x∈(x0,+∞)时,h(x)＞0,则f'(x)＞0,f(x)单调递增。

故M(x)在(0,ln 3]上单调递减,M(x)≥M(ln 3)=ln 3-3,M(x)＜M(0)=-1,ln 3-3≤a＜-1。

注意：h(x0)=0,即的应用。另外,本题中先求出零点x0的取值范围,再建立关于a的函数,从而得到a的取值范围。

利用导数解决含参不等式恒成立问题的两种常用方法：(1)分离参数法,将原不等式分离参数,转化为求不含参数的函数的最值问题,利用导数求得所求范围,一般地f(x)≥a恒成立,只需f(x)min≥a,而f(x)≤a恒成立,只需f(x)max≤a;(2)函数思想法,将不等式转化为含待求参数的函数的最值同题,利用导数求该函数的极值(最值),然后构建不等式求解。

有些题目无法用分离参数求得,或者比较复杂,这时只能用分类讨论的方法求解。几种方法要灵活运用。

例5已知函数,且曲线y=f(x)在点(1,f(1))处的切线方程为y=x-1。

(1)求实数m,n的值及函数f(x)的最大值;

解析：(1)函数f(x)的定义域为(0,+∞),f'(x)=。因为f(x)的图像在点(1,f(1))处的切线方程为y=x-1,所以

令f'(x)=0,得x=e。

当0＜x＜e时f'(x)＞0,f(x)单调递增;当x＞e时f'(x)＜0,f(x)单调递减。

所以当x=e时f(x)取得最大值,最大值为

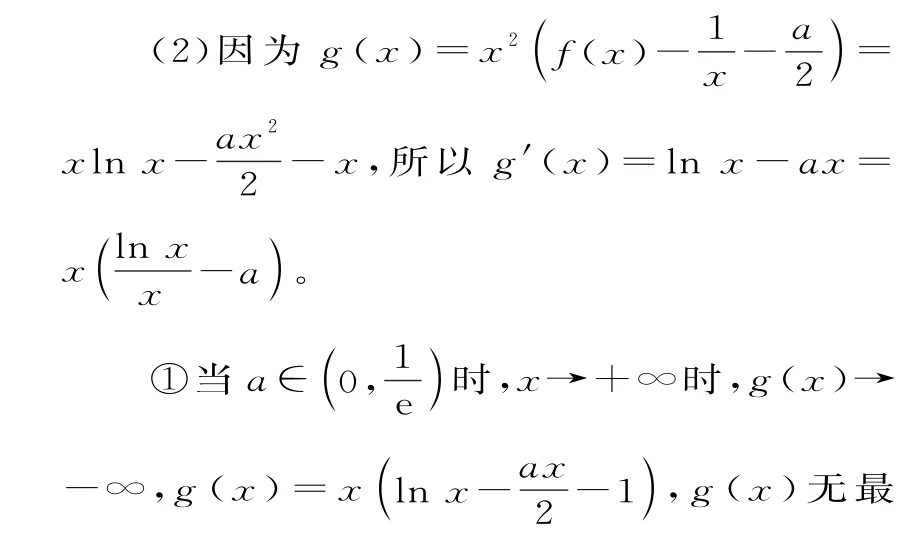
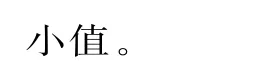
②当a=0时,g'(x)=lnx,由g'(x)＞0,得x＞1;由g'(x)＜0,得0＜x＜1。

所以g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,g(x)的最小值b=g(1)=-1。

当x∈(0,t)时,g'(x)＜0,当x∈(t,+∞)时g'(x)＞0,所以g(x)在(0,t)上单调递减,在(t,+∞)上单调递增,g(x)的最小值注意利用lnt=at代入,可换掉字母a得到一个关于t的函数,令在上单调递减。

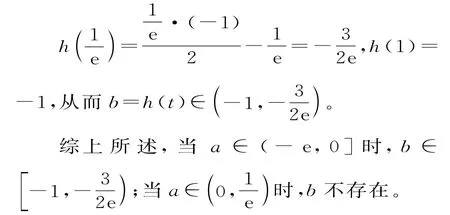
函数、导数、不等式的综合问题是近几年高考的热点问题,这类问题往往以“参数处理”为主要特征,“导数运用”为主要手段,“函数的单调性、极值、最值”为结合点,常涉及导数、不等式、方程等多方面的知识,需要综合运用化归与转化、分类讨论、数形结合等数学思想方法求解。