刻意训练 你要的“几何大法”就来了

晏畅

摘 要：为了提高学生的模型意识和发散性思维，本文通过对2019年辽宁省沈阳市中考试卷的第16题的解法探究，以“一题多解”的方式，对问题进行多角度、多层次分析，剖析如何“刻意训练”学生运用模型思想去探究几何问题的解题思路.

关键词：模型思想;解题指导;一题多解

数学家华罗庚曾说：“当遇到复杂的数学问题时，要善于退，足够的退，退到最简单而又不失关键的地方.”其实几何没有我们想象的那么难，核心点在于如何把复杂几何图形的关键信息抽离成几个基础几何图形，再通过辅助线转化成我们熟悉的几何模型，也就是《数学课程标准》强调的模型思想.本文以2019年辽宁省沈阳市中考试卷的第16题为例，通过“一题多解”对问题进行多角度、多层次分析，谈谈如何“刻意训练”学生运用模型思想去探究几何问题的解题思路.

1 试题呈现

题目 如图1，正方形ABCD的对角线AC上有一点E，且CE=4AE，点F在DC的延长线上，连接EF，过点E作EG⊥EF，交CB的延长线于点G，连接GF并延长，交AC的延长线于点P，若AB=5，CF=2，则线段EP的长是.

此题以正方形为背景，涵盖了等腰直角三角形、直角三角形、全等三角形、相似三角形的知识，综合性强，解题难度较大，如何快速切入，模型思想为我们插上异彩纷呈的思维翅膀，接下来我们在解法中展翅翱翔.

2 解法探究

本题的实质是：45°特殊角，等腰直角三角形问题，比例线段问题.因此可以依托常见的模型，打开解题思维的闸门：即45°角+“母子型”相似、“一线三等角”模型、“手拉手”模型、建系法.

2.1 45°角+“母子型”相似

解法1 如图2，过点F作FH⊥PE于点H.

因为四边形ABCD是正方形，AB=5，

所以AC=5 2，∠ACD=∠FCH=45°.

易求EC=4 2，EH=5 2.

在Rt△EFH中，EF2=EH2+FH2=（5 2）2+（2）2=52.

因为∠GEF=∠GCF=90°，

所以E，G，F，C四点共圆.

易证△CEF∽△FEP.

可得EF2=EC·EP.

所以EP=524 2=13 22.

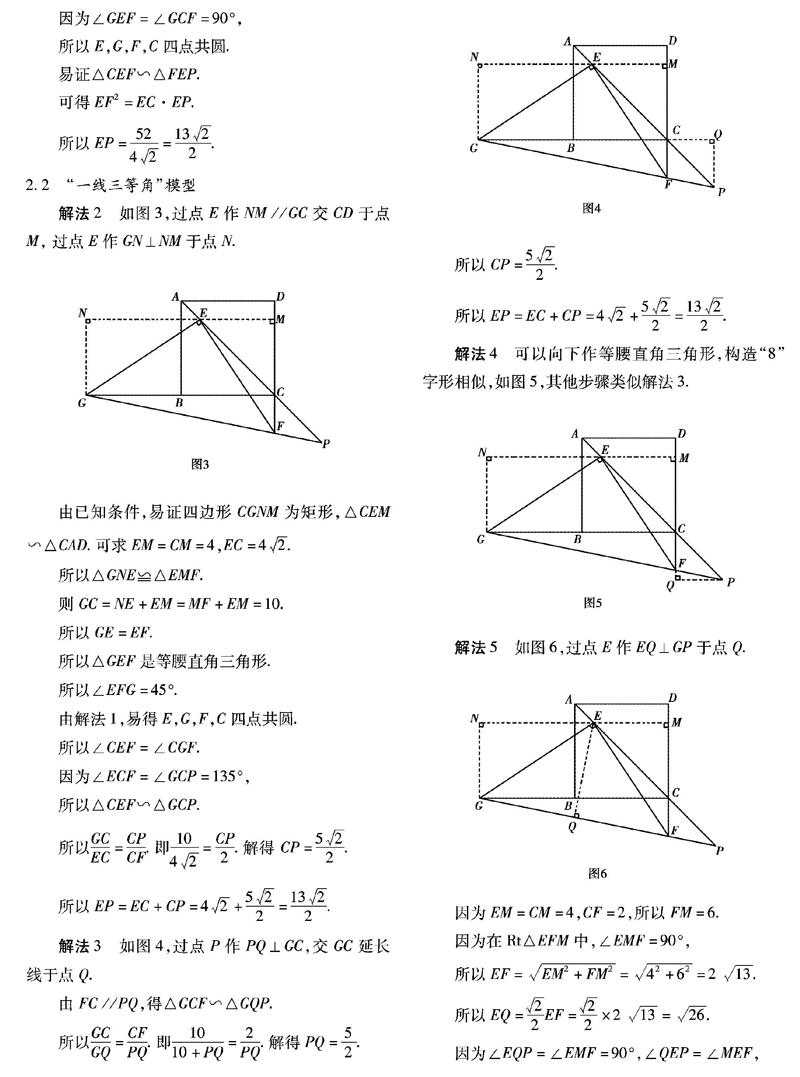
2.2 “一线三等角”模型

解法2 如图3，过点E作NM//GC交CD于点M， 过点E作GN⊥NM于点N.

由已知条件，易证四边形CGNM为矩形，△CEM∽△CAD.可求EM=CM=4，EC=4 2.

所以△GNE≌△EMF.

则GC=NE+EM=MF+EM=10.

所以GE=EF.

所以△GEF是等腰直角三角形.

所以∠EFG=45°.

由解法1，易得E，G，F，C四点共圆.

所以∠CEF=∠CGF.

因为∠ECF=∠GCP=135°，

所以△CEF∽△GCP.

所以GCEC=CPCF.即104 2=CP2.解得 CP=5 22.

所以EP=EC+CP=4 2+5 22=13 22.

解法3 如图4，过点P作PQ⊥GC，交GC延长线于点Q.

由FC//PQ，得△GCF∽△GQP.

所以GCGQ=CFPQ.即1010+PQ=2PQ.解得PQ=52.

所以CP=5 22.

所以EP=EC+CP=4 2+5 22=13 22.

解法4 可以向下作等腰直角三角形，构造“8”字形相似，如图5，其他步骤类似解法3.

解法5 如图6，过点E作EQ⊥GP于点Q.

因为EM=CM=4，CF=2，所以FM=6.

因为在Rt△EFM中，∠EMF=90°，

所以EF=EM2+FM2=42+62=2 13.

所以EQ=22EF=22×2 13=26.

因为∠EQP=∠EMF=90°，∠QEP=∠MEF，

所以△EQP∽△EMF.

所以EQEM=EPEF.即264=EP2 13.解得EP=13 22.

2.3 “手拉手”模型

解法6 如图7，过点E作EH⊥EC于点E，交GC于点H.

根据“手拉手”模型，易证△EGH≌△EFC.

所以△GEF与△HEC是等腰直角三角形.

所以GH=CF=2.

又因为HC=2EC=8，∠GCF=90°，

所以GF=GC2+CF2=102+22=2 26.

所以EF=22GF=2 13.

因为∠ECF=∠GCP=135°，所以△CEF∽△FEP.

所以EF2=EC·EP.

所以EP=524 2=13 22.

2.4 建系法

解法7 如图8，以点C为坐标原点，GC所在直线为x轴建立平面直角坐标系.过点P作PQ⊥NM，交EM延长线于点Q.

所以点C的坐标为（0，0），点E的坐标为（-4，4），点G的坐标为（-10，0），点F的坐标为（0，-2）.

所以直线EC的解析式为y=-x，直线GF的解析式为y=-15x-2.

联立方程组可解得点P的坐标为（52，-52）.

所以EQ=QP=132.

因为在Rt△EQP中，∠EQP=90°，

所以EP=EQ2+QP2=1322+1322=13 22.

3 解题感悟

很多同学解这道题时感觉很熟悉，这是由于我们在平时解题中涉及很多和它同类或者方法一样的题目，但是考试时会出现见过或做过的题目仍然不会.究其本质，原因在于我们在平时数学的学习中没有很好地进行归纳总结，没有深入地了解每一个知识点，每一个条件如何考察，如何使用，也没有很好地建立起自己的一套几何模型体系，所以见到不同的条件就找不到思考方向.所以在解题教学中，教师应该教会学生如何运用化归思想，退居本质，观察图形特征，联想相关知识模型，构造适当的几何基本图，从条件出發推理得到新结论，把难题转化为易于解决的问题.这种意识和习惯要进行系统化的科学指导和长期练习才能形成，就是所谓的“刻意训练”.

绝大多数几何题都可以从中找到相应的几何模型或策略方法.几何模型是解决几何问题的利刃，策略方法是教师指导学生如何通过“刻意训练”学会选择“利刃”从而优化解法，一旦熟练掌握，那么解决难题就是水到渠成自然而然的事了.

参考文献：

[1]陈锋，薛莺，童伟伟.多元化的“微探究”：从机械记忆走向理解建构[J].中学数学，2013（18）：76—78.

[2]李郊.构造法的应用[J].中学数学，2012（03）：86.

（收稿日期：2019-07-24）