基于HALRTC理论的短时交通流预测算法

教欣萍，王江锋*，陈磊，高志军，董佳宽，黄海涛，叶劲松

(1.北京交通大学 交通运输学院 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044;2.交通运输部科学研究院，北京 100029)

智能交通协同诱导技术为有效改善高速公路出行服务水平提供了有力支撑，作为其中关键技术的短时交通流预测，可实现交通流态势实时预估，为出行者提供更可靠的出行路径参考方案。但是，交通流蕴含的不同时间维度信息对其短时预测结果具有显著影响[1-2]。

目前，短时预测方法多考虑交通流低维信息，易使其信息丢失导致无法满足预测精准度的要求。国内外学者陆续将卡尔曼滤波理论、K近邻法、ARIMA模型等用于短时交通流预测[3-5]。文献[6-9]基于卡尔曼滤波方法、K近邻法提出一些改进算法用于优化预测性能；文献[10-14]基于小波分析、高斯回归过程、分形理论、突变理论、混沌理论等方法进行了短时交通流预测；神经网络具有高度非线性的动力学系统，有强大的非线性拟合能力，文献[15-18]将神经网络方法应用于短时交通流预测，其中BP神经网络应用最为广泛；随着组合模型的广泛运用，文献[19-21]将多种模型组合应用于短时交通流预测。传统短时交通流预测算法大多将交通流数据视为一维时间序列，这种线性或平面数据表征方法忽略了交通流数据在多时间维度的信息挖掘，难以有效利用交通流数据的内部结构性和规律性。

近年来，张量作为一种高阶数据空间的多重线性映射模型，可以深层挖掘数据内部结构与规律，已经成为大数据处理领域的研究热点[22]，国内外学者在张量理论研究方面积累了良好的研究基础[23-25]。由于交通流数据在不同时间维度上具有很强的规律性，为张量理论应用于短时交通流预测提供了理论基础。本文基于实际交通流速度数据，挖掘其在不同时间维度的规律特征，建立基于高精度低秩张量填充(high accuracy low-rank tensor completion，HALRTC)理论的短时交通流预测算法，提升短时交通流预测的预测效果与精度。

1 动态张量矩阵构建

为了充分挖掘交通流数据在不同时间维度上的规律性，实现滚动式数据输入预测未来时间段交通状态，将短时交通流预测问题转化为动态张量填充问题。以京港澳高速公路杜家坎路段2017年4月至6月共10周的速度数据为例，构建了周维度×天维度×时段维度的三维动态张量矩阵模型，如图1所示。实际交通流数据从每日零点开始采集，每5 min为一时段，一天共采集288个时段数据。

图1 动态张量模型示意图

2 短时交通流预测算法

结合图1构建的动态张量矩阵模型，设计基于HALRTC理论的短时交通流预测算法。该算法按照运算逻辑，包括算法函数确定、增广拉格朗日函数转换和迭代求解3个步骤，即可获得短时交通流的预测结果。

2.1 算法函数

设A为由交通流速度数据构成的三维动态张量，大小为I1×I2×I3。同样设置大小为I1×I2×I3的非负权重张量W，权重张量中元素赋值如下：

(1)

引入3个相同大小的三维张量M1、M2及M3，则算法函数可定义为张量核范数最小化问题：

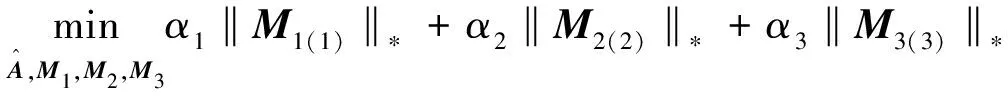
(2)

式中，M1(1)为M1按模式I1×(I2I3)展开所得数值矩阵，同理M2(2)、M3(3)为M2、M3按模式I2×(I1I3)、(I1I2)×I3展开所得数值矩阵。参数α1、α2及α3满足α1+α2+α3=1，实际运算中3个参数常取相等数值。

2.2 增广拉格朗日函数

对算法函数进行推导，可得其增广拉格朗日函数如下：

(3)

式中，Y1、Y2、Y3为额外变量，参数ρ随迭代次数而逐渐增加，通常设ρ0=ρ，有ρk+1=tρk，t∈[1.15,1.25]。

借助交替方向乘子法思路，可对式(3)进行迭代：

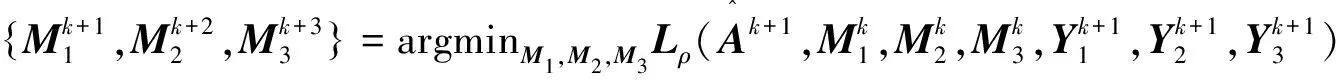
(4)

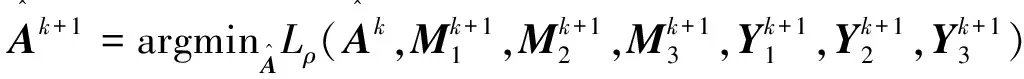
(5)

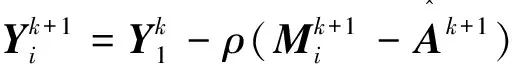
(6)

交替方向乘子法可确保增广拉格朗日函数中迭代过程的收敛性，加快参数迭代计算过程。

2.3 迭代求解

对于M1、M2及M3，每次更新有如下优化问题：

(7)

通过奇异值收缩算子计算可得式(7)的闭形式解为：

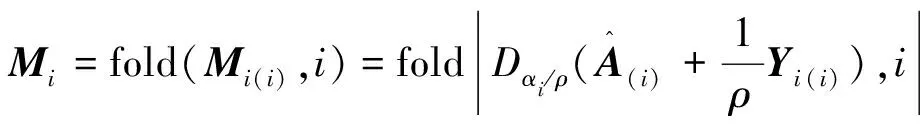
(8)

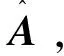
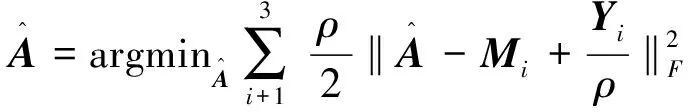
(9)

由一阶最优性条件可得其解为：

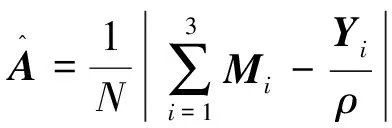
(10)

则N阶张量X∈RI1×I2×…×IN的HALRTC算法函数与增广拉格朗日函数可描述为：

(11)

s.t.X=Mi,i=1,…，n，

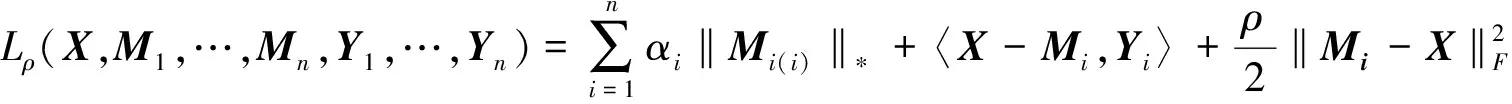
(12)

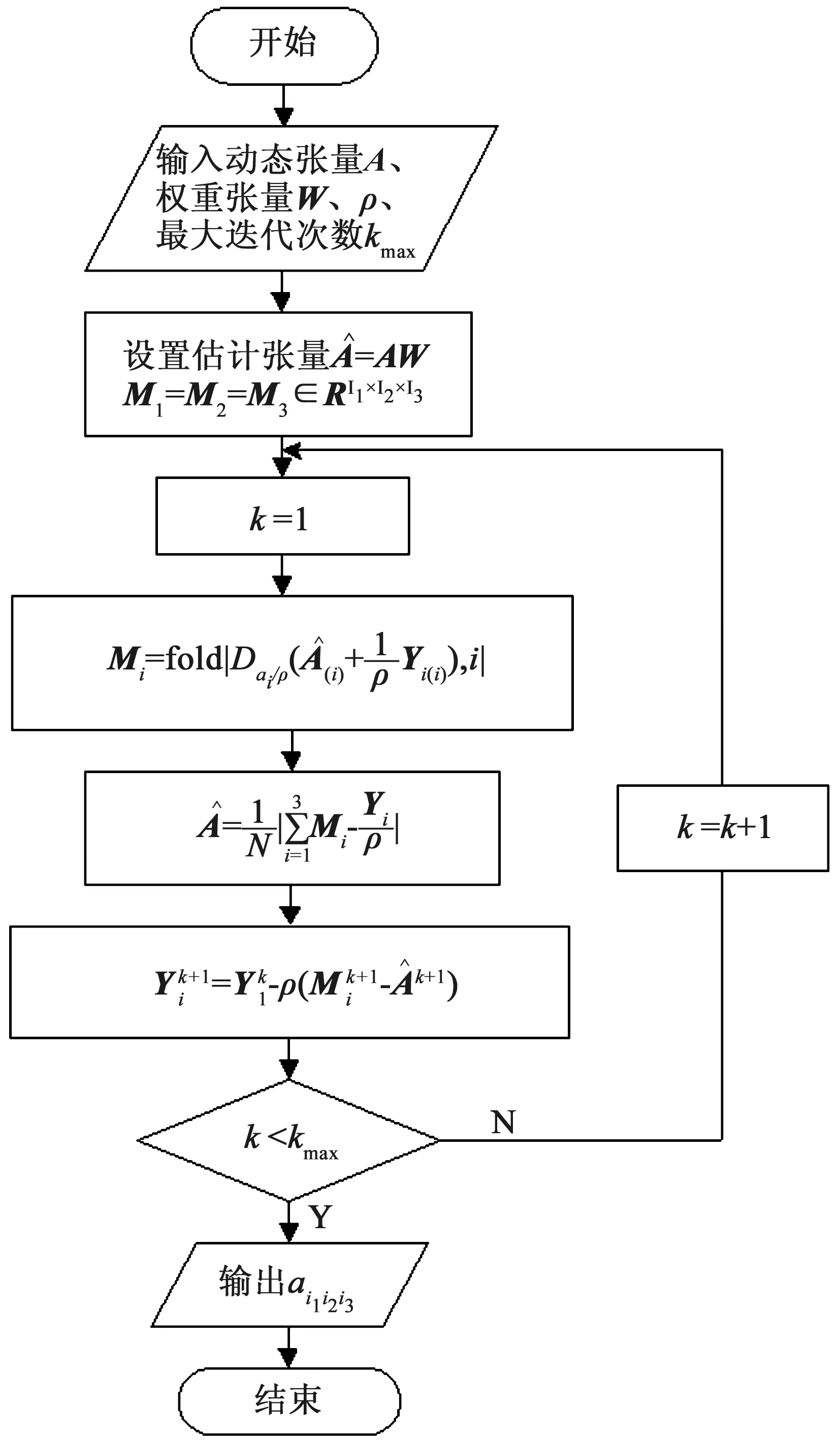
图2 HALRTC预测算法逻辑流程图

3 实例分析

利用京港澳高速公路杜家坎路段2017年4月至6月速度数据对所提出HALRTC算法进行实证分析，分别进行天维度、周维度预测精度分析，以及缺失数据下该算法与其他经典算法的精度对比分析。

3.1 天维度预测精度

针对天维度，分析算法在周维度与时段维度预测精度的变化规律，选择平均绝对误差(mean absolute error，MAE)为评价指标。图3为不同周维度、时段维度下第10周周一交通流速度预测精度结果。从时段维度上看，预测精度随着时段维度的增大而增大，在时段维度为18或20时预测精度呈现平面状态，MAE指标稳定在2.8%左右；从周维度上看，MAE在周维度大于6后表现出略微增长趋势，说明所提出预测算法能够基于较少历史数据较快达到良好的预测效果。

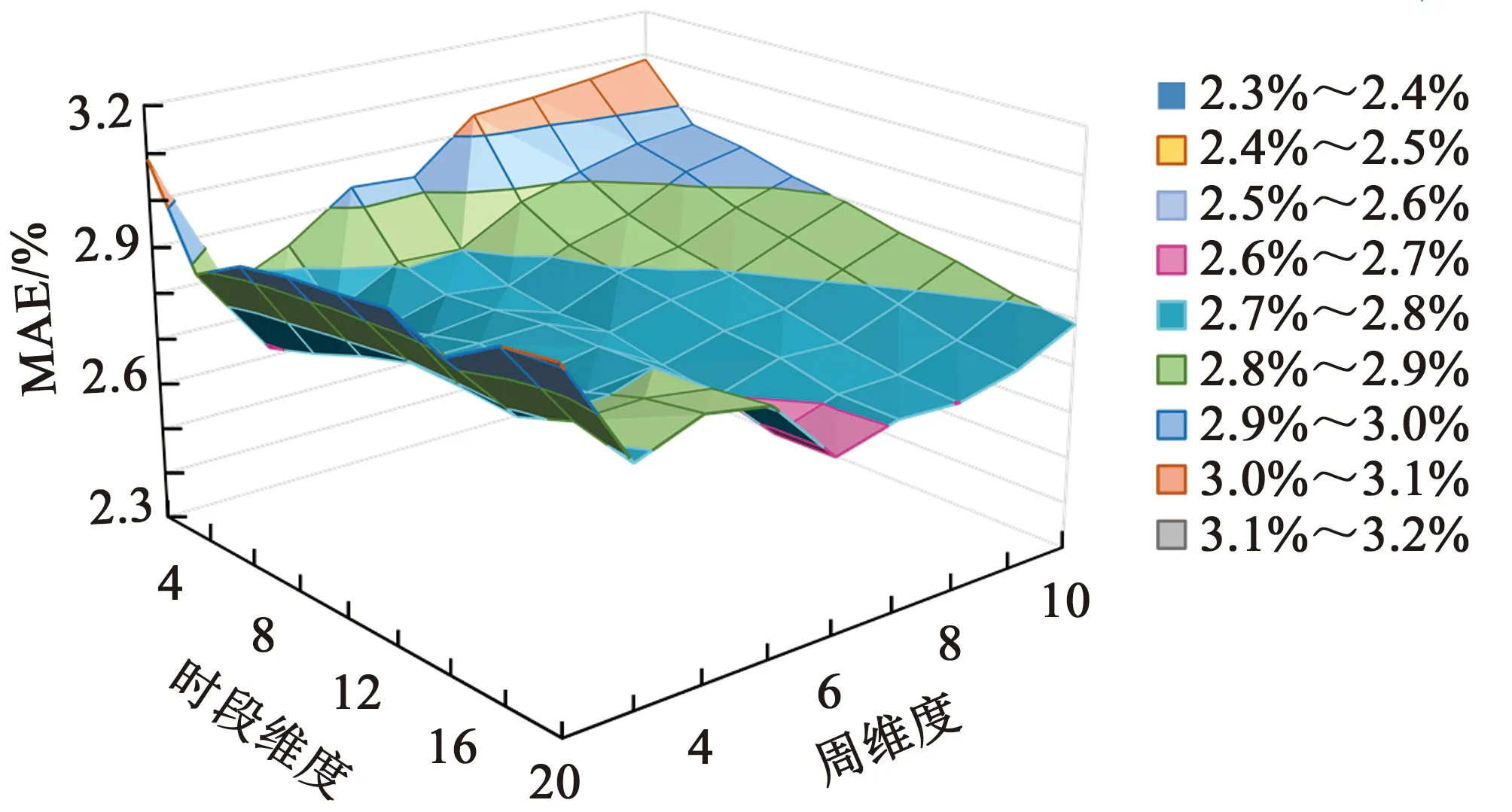
图3 天维度预测精度变化趋势

3.2 周维度预测精度

针对周维度，分析算法在同周不同日的预测精度。表1为不同周维度、时段维度下第11周共计7 d的速度数据预测精度结果，MAE指标平均值约为3.6%。其中非工作日预测精度较低，说明当速度数据波动加大时，所提出算法需要更多历史数据才能获得良好预测效果。

表1 算法第11周速度预测精度结果

为深入分析速度数据波动较大时所提出预测算法的预测性能，分别选取第11周周四与周日作为分析对象，算法的预测精度结果如图4所示。结果表明，当出现明显速度波动时，所提出算法依然能够有效预测速度波动，即使在速度波动频繁的周日，算法也能取得良好的预测效果，成功实现对两个速度高峰时期的曲线跟踪。

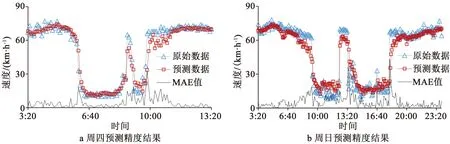
图4 算法针对速度波动的预测结果

3.3 缺失数据下预测算法精度对比分析

针对不同比例缺失数据，分析所提出短时交通流预测算法的精度变化情况。表2给出了不同比例缺失数据情况下所提出算法的预测精度结果，预测精度随缺失数据比例增大而呈现下降趋势，说明所提出算法对数据缺失较为敏感，在短时交通流预测时也会对数据完整性有一定要求。对缺失数据进行预处理后，所提出算法的预测精度得到大幅提升。

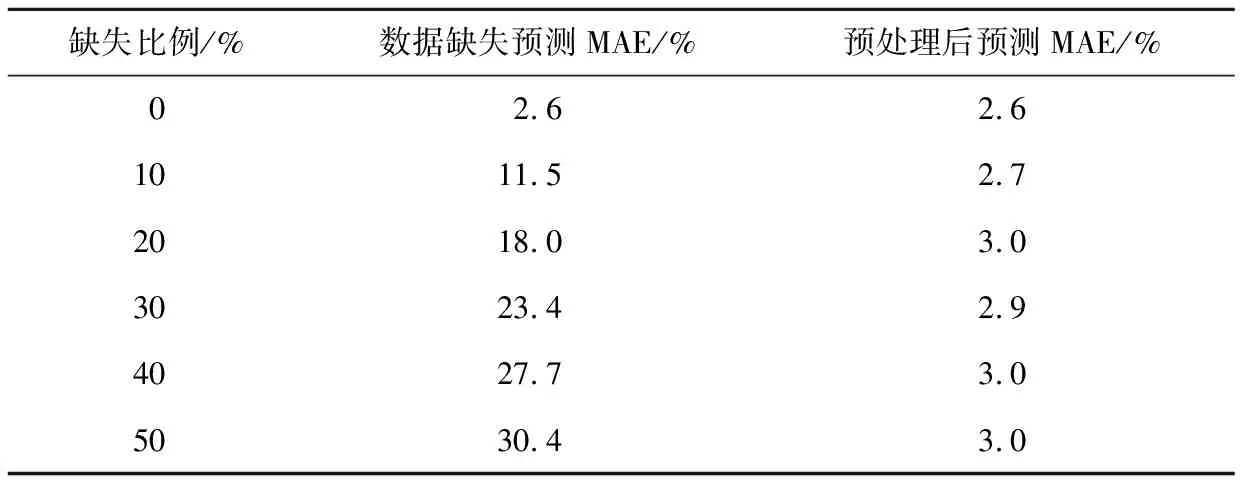
表2 缺失数据下所提出算法预测精度结果

选择ARIMA、BPNN和KNN作为比较算法，进一步分析不同比例数据缺失情况下所提出算法的预测性能。为保证算法预测结果的有效性，利用不同比例缺失数据分别进行4种算法预测性能测试，重复进行10次，测试结果的MAE指标平均值如图5所示。随着数据缺失比例增大，4种算法的预测精度均有所下降。相比较而言，本算法的预测效果较好，明显低于其他3种经典算法的预测误差,算法表现出更好的预测精度。

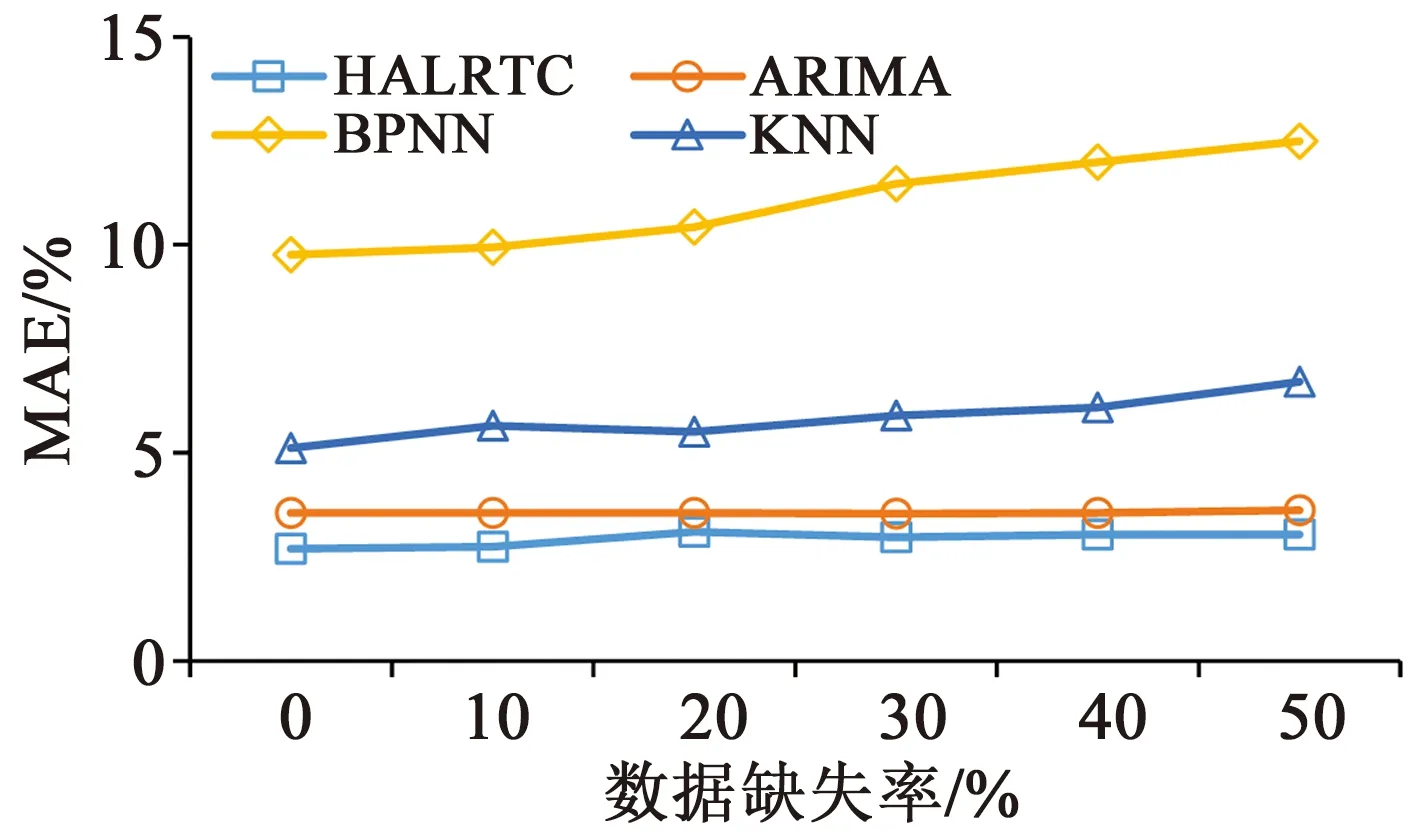
图5 缺失数据下4种算法预测精度结果

4 结论

针对交通流所蕴含的不同时间维度信息特征，本文从周维度×天维度×时段维度构建了动态张量模型，提出一种基于HALRTC理论的短时交通流预测算法。所提出算法可实现针对工作日与非工作日的交通流有效预测，MAE指标平均值约为3.6%，并能及时跟踪交通流波动性。在缺失数据情况下，所提出算法预测精度随数据缺失比例增大而降低，但相较于3种经典预测算法可表现出更好的预测精度。本文的算法效率有待提高，同时选取的路况比城市道路简单，未来可以将HALRTC理论应用于城市道路并改进算法的效率。