电动公交车线路和充电设施及策略规划方法研究

姜岚清，张勇

(苏州大学 轨道交通学院，江苏 苏州 215131)

电动汽车替代传统燃油汽车已成为汽车产业可持续发展的必然趋势，也是解决能源消耗与环境污染问题的有效手段。电动公交车具有固定的行驶路线、发车时间以及停车场所，能够很好地适应电动汽车续航里程短、充电时间长的特点，使得电动公交车成为电动汽车在中国市场推广的先驱。在国家的大力支持和推动下，我国电动公交事业进入快速发展时期，2015年交通部出台的《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》，指出到2020年城市新能源公交车将达到20万辆[1]。目前，国内主要城市新能源公交车占比都已达到40%以上，其中深圳在2017年已实现公交100%车电动化，根据各地规划要求，到2020年全国公交车电动化率有望达到70%。由于电动公交车与汽油车补能方式不同，时间差别大，因此要求电动公交线路设计时要考虑充电桩配置要求。但是从目前各地市电动公交车充电设施建设情况来看，由于多依赖经验配置、缺乏理论指导，充电桩配置数量相差较大，有的按照“一车一桩”配置，有的按照“四车一桩”配置，有的按照“六车一桩”配置，造成车桩配置不合理[2]。因此，发展电动公交事业，首先要对其充电基础设施的规划建设问题进行研究。

目前，一些学者对电动公交基础设施规划问题进行了研究。陈伟等[3]根据充电站内充电桩容量、电动公交车参数计算所需配置充电桩的数量，但没有考虑公交车充电排队情况对公交运营的影响。为了讨论公交车充电排队情况，蔡子龙等[4]以充电桩数量最小为目标，在公交枢纽站内建立公交充电排队系统模型，对直流快速充电模式下高峰和平峰期充电设施最优配置进行了研究。但是该模型并没有考虑公交运营成本。为了详细分析运营成本问题，Zou等[5]研究电动公交换电站配置优化问题，以服务可用性为约束、运营成本最小为目标建立模型，优化站内充电桩，并进行了案例分析。Wang等[6]以年总运营成本最小为目标，建立了一个优化电动公交车充电时刻表的模型，模型可以为充电站位置、数量和运营提供相应的决策支持。Li[7]以公交车辆最大行驶里程为约束，建立车辆时刻表模型，分析了电动、燃油、混合动力公交车的总运营成本，并提出了列代算法求解时刻表问题，研究结果表明，电动公交车使用换电形式将不会显著增加车队车辆数量。上述文献侧重充电桩配置数量的研究，但同时也有针对充电策略以及政府政策的影响分析。Qin等[8]模拟了佛罗里达州塔拉哈西一天的电动公交运营与充电需求情况，并以减少充电需求为目标，确定了最佳的充电策略。Rick等[9]以量化形式分析了日间停车和免费停车政策对充电行为的影响，并指出在设计政策时应考虑充电行为与政策之间的相互影响关系。

以上文献，从不同角度基于确定的运营条件优化充电设施配置或充电策略等，但没有考虑公交线路自身运营条件对充电站及充电桩配置的影响。对于公共交通线路设计与运营优化等问题的研究也有很多。Wirasinghe等[10]确定了以公交运营成本和客运时间成本之和最小化为目标的最优公交服务特性，分析了站间距、接驳巴士区域边界和车头时距等运营参数，给出了简明的最优参数结果。Daganzo等[11]详细分析了两点系统、交通走廊系统、二维平面网络系统在理想与现实情况下的公共交通运营原则与优化方法。Constantin等[12]建立了以乘客乘车时间最小为目标，车辆数量为约束条件的非线性发车频率优化模型。Ceder[13]将公交调度时刻表编制问题作为一个多目标优化问题，假定乘客到达服从均匀分布，乘客等车时间为发车间隔时间的一半，在此基础上构建公交发车时刻优化模型。

本文综合考虑充电站及充电桩配置与公交线路运营特征参数设计两者的相互影响，在公共交通走廊上，以社会福利最大化为目标建立模型，考虑线路运量约束和车辆充电站内充电等待时间约束，优化站点数量及位置、发车频率、票价以及线路首末端充电桩数量等。文中还考虑不同的充电策略对充电站内车辆充电排队等待时间的影响。

1 模型构建

在一条公交走廊上，电动公交车按发车间隔发车，沿公交线路来回循环运行，当电量不足时到首末端充电站内充电，为了确定公交线路最优的站点数量及位置、发车频率、票价、车队规模与充电桩数量，构建了如下的优化模型。

1.1 基本假设

为方便建模，进行如下假设：

A1.假设所研究的线性交通走廊长度为B，公交线路总长度等于走廊长度；

A2.电动公交车票价采用单一票价制度；

A3.用线性弹性需求函数来表示乘客对线路服务水平的反应；

A4.乘客选择最近的公交站点乘车；

A5.公交线路一端发车；

A6.所有电动公交是相同的，电池充电电量与充电时间成正比，电池电量消耗与行驶里程成正比。

1.2 站点乘客需求分析

如图1所示，在长度为B的线性交通走廊上布设一条电动公交线路，线路上有N个公交站点，Ds表示第s个站点到第一个站点的距离，DN表示线路总长度。用ls表示s站点和s+1站点之间客流分界线，即当乘客位于(s,ls)之间时，表示乘客去s站点乘车，当乘客位于(ls,s+1)之间时，到s+1站点乘车。Ls表示ls到站点1的直线距离。根据A4可知，ls位于s站点和s+1站点正中间，用公式表示为：

(1)

其中，D1=0,LN=DN，在不影响结果的情况下，为了方便下文公式表示令L0=0。

用q(x,s)表示在x处到站点s乘车的乘客数量，根据A3可知：

q(x,s)=g(x)(1-eaus(x)-ewws-eff-evVb)，∀x∈[0,B],∀s=1,2,…,N，

(2)

其中：g(x)表示在x处人口密度分布；us(x)表示乘客从x处到站点s所用的时间，下文简称为访问时间；ws表示乘客在s站点的平均等待时间；f表示票价；Vb表示公交车最大行驶速度(Vbmax)与实际平均行驶速度(Vb1)之差；ea、ew、ef、ev分别表示us(x)、ws、f以及Vb的弹性系数。

为了保证在x处到站点s乘车的乘客数量大于等于0，应满足条件

0≤1-eaus(x)-ewws-eff-evVb≤1,∀x∈[Ls-1,Ls],s=1,2,…,N。

(3)

根据A4，公式(3)中乘客访问时间us(x)可以通过乘客所在位置x与s站点之间的距离以及乘客步行速度(Va)计算得到，公式表示为：

(4)

乘客在站点s的等待时间ws计算表达式为：

ws=αH, ∀s=1,2,…,N，

(5)

其中：H表示发车时间间隔；α表示系数，可由发车间隔所服从的分布和乘客到达时间间隔分布决定。当公交线路发车间隔和乘客到达时间间隔均服从均匀分布时，α=0.5。

电动公交车的实际平均行驶速度Vb1与站点个数N有关，假设各站点停靠时间固定为β，电动公交在路段上最大行驶速度为Vbmax，则电动公交车的实际行驶速度Vb1可表示为：

(6)

因此，Vb表示为：

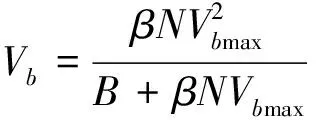
(7)

由此可得各站点乘客数量Qs为：

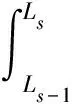
(8)

将公式(2)、(4)、(5)、(7)代入到公式(8)中得到各站点乘客数量Qs为：

(9)

图1 线性交通走廊上公交线路布局示意图

1.3 消费者剩余

由于公共交通是公益性的，因此以社会福利最大化作为决策者的目标更为合理。社会福利(W)由消费者剩余(G)和公交运营商纯利润(π)两部分组成，即：

W=G+π。

(10)

接下来分别对消费者剩余和公交运营商纯利润进行讨论。

首先定义站点s的消费者剩余Gs。根据公式(2)可以得到关于票价的需求密度函数为：

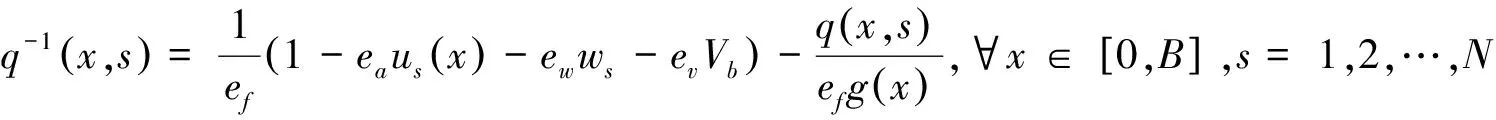
(11)

因此对于乘客从x处到s站点乘车的消费者剩余G(x,s)为：

(12)

所以s站点的消费者剩余Gs为：

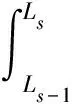
(13)

所以总消费者剩余为：

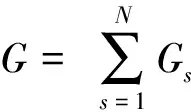
(14)

1.4 运营商纯利润

运营商纯利润(π)等于总收益(R)减去总成本(C)，即：

π=R-C，

(15)

其中，总收益等于各站点乘客票价收益，即：

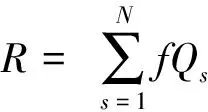
(16)

其中，Qs由公式(8)得到。

运营商的总成本包括购车成本Cb、运营成本Co、充电站及充电桩配置成本Ce、充电等待时间成本Cw4个部分组成，公式表示为：

C=Cb+Co+Ce+Cw。

(17)

购车成本用购买一辆车价格cb乘以车辆总数F，用公式表示为：

Cb=cb·F。

(18)

运营成本仅考虑电动公交车每天车辆运行所消耗的电量成本，根据A6可得：

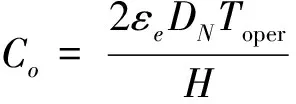
(19)

其中，Toper表示线路每天运行总时间，εe表示单位行驶里程耗电量成本。

充电站和充电桩配置成本包括固定成本与可变成本两部分，公式表示为：

Ce=Δ0+cΔ，

(20)

其中，Δ0是充电站系统建设固定成本，Δ表示一个充电桩的成本，c表示充电桩总数量。

充电等待时间成本由总充电等待时间乘以单位等待时间成本η。总充电等待时间等于每辆车平均充电等待时间乘以总车辆数。

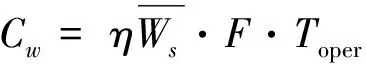
(21)

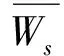
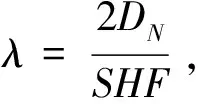
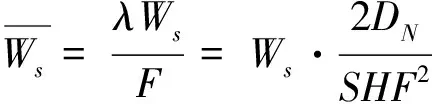
(22)

其中，Ws根据有限源顾客排队模型(M/M/c/∞/F)得到，具体推导公式如下：

(23)

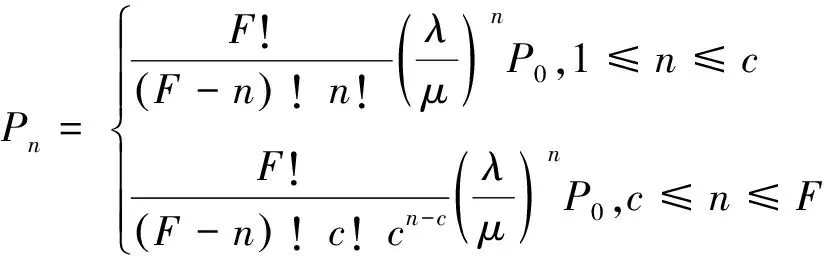
(24)

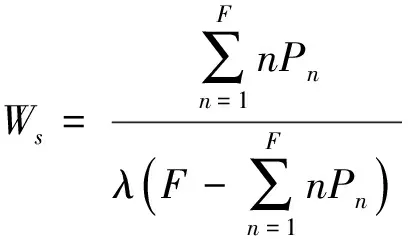
(25)

其中，ρ=λF/cμ，λ表示车辆到达率，μ表示充电桩充电服务速率，F表示车队总数量，c表示充电桩数量。

由公式(17)～(25)得到运营商每天总成本为：

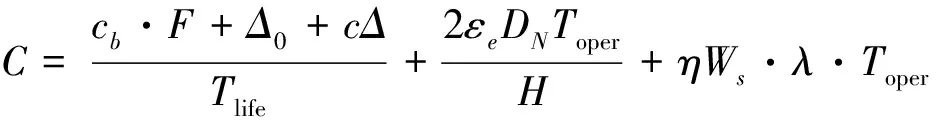
(26)

将公式(14)、(15)、(16)、(26)代入公式(10)得到社会福利为：

(27)

1.5 社会福利最大化模型

根据上文的分析，得出社会福利最大化模型为：

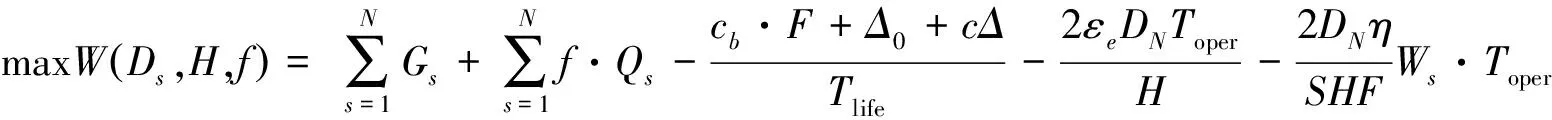
(28)

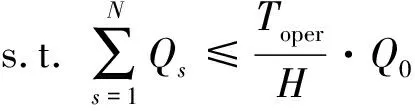
(29)

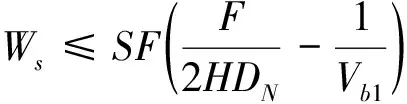
(30)

其中，公式(29)是运量约束条件，表示运量小于运力，其中Q0表示电动公交车的最大装载量。公式(30)是充电等待时间约束，推导过程如下：

(31)

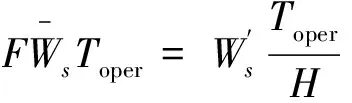
(32)

(33)

由于t0≥0，因此有

(34)

2 充电策略对比研究

不同城市电动公交车充电策略是不同的，基本可以分为两种充电方式：(1)公交车持续运营直到电量不足再充电；(2)当车辆一次运行结束后，只要有空闲充电桩则充电。本文基于以上两种充电策略，对以下两种情形进行对比分析研究。

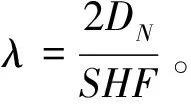
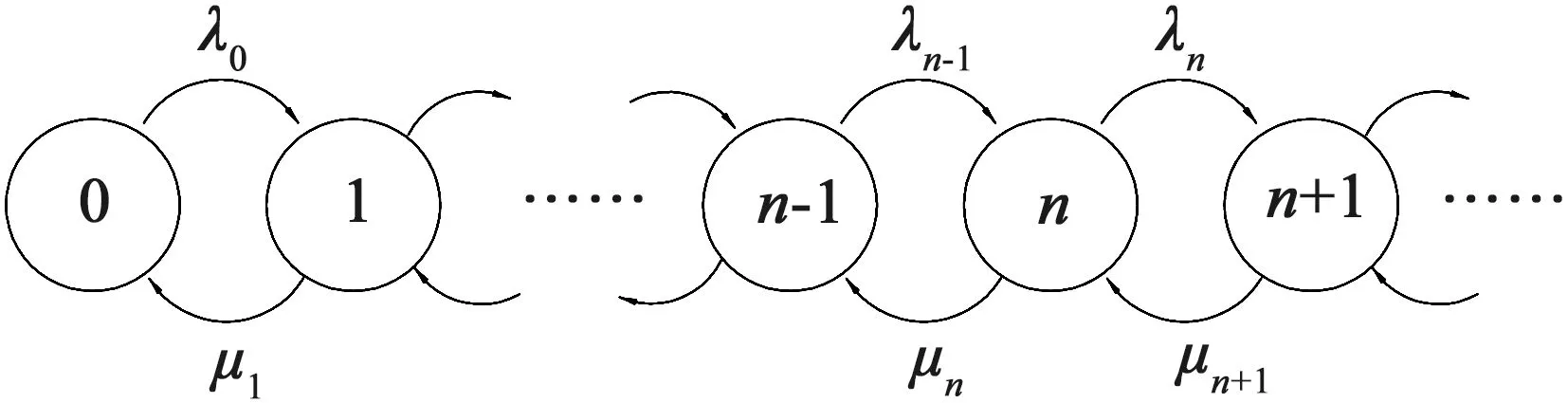
图2 充电车辆状态转移图

情形二：电动公交车充电规则是当车辆一次运行结束到达充电站时，若有空余充电桩则立即充电，若没有空余充电桩，则根据车辆剩余电量是否能满足下一次循环运行来决定是否排队等待充电。将充电站看成一个排队系统，系统里面的车辆数用n表示，λn表示系统中有n辆车时的到达率，μn表示系统中有n辆车时的离开率，pn表示系统中有n辆车的平稳状态概率。图2为充电站内车辆队列状态转移图。

在平稳状态条件下，对于n>0，流入和流出状态n的期望速率必相等，又有状态n只能变成状态(n-1)和(n+1)的事实，因此可得到状态n的平衡方程为：

λn-1pn-1+μn+1pn+1=(λn+μn)pn。

(35)

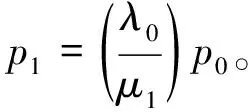
一般地，可用归纳法得到：

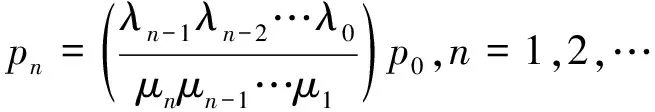
(36)

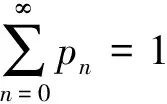
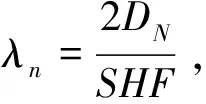
(37)

将公式(37)代入公式(36)即可得到状态概率pn的值，又有Little公式：

(38)

其中，L系统表示充电站系统中充电车辆的期望数，λeff表示充电车辆有效到达率。因此可以算出充电站内车辆充电等待时间Ws，其中有效到达率计算式为：

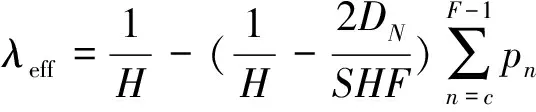
(39)

3 求解算法

根据公式(28)～(30)提出的社会福利最大化模型，以构造拉格朗日函数法设计求解算法，在算例中将本算法与遗传算法进行对比分析，下面分别介绍拉格朗日函数法求解算法与遗传算法。

3.1 拉格朗日函数法求解算法

针对所提出的社会福利最大化模型，构造拉格朗日函数，寻求规划问题的K-T点，运用KKT条件和约束条件建立方程组，并讨论乘子的取值以确定最优性条件[14-15]。分别对变量和乘子求偏导，结果如下：

(40)

基于公式(40)设计求解方法，具体步骤如下：

Step2：更新设计变量。根据公式(40)依次更新发车频率、票价和站间距。

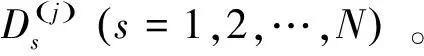
Step4：终止检查。如果连续迭代得到的目标函数值足够接近，则终止算法并输出变量最优解{D*,H*,f*,c*,F*}和最大社会福利值W*。否则，令j=j+1并转到Step2。

在具体应用中，基于拉格朗日函数法的优化算法流程图如图3所示。

值得注意的是，以上的算法步骤是基于确定的站点个数，求解对应站点个数的最优解。由于实际中站点个数是有限的，因此可以通过对比不同站点个数情况下最优社会福利值，得到最终解。

3.2 遗传算法模型求解

遗传算法是一种智能算法，一般被用来求解VRP问题，Holland教授在1975年首先提出，是一种基于自然选择和基因遗传学的全局搜索方法，通过选择、交叉、变异等遗传算子来仿真生物的进化过程，利用适应度函数来表示染色体的优良性。遗传算法模拟达尔文的自然进化论和遗传变异理论，适合求解复杂的多极值优化问题和组合问题，具有广泛的应用价值[16-17]。图4为遗传算法流程图，编码采用的是二进制Gray编码，文中社会福利值即作为个体适应度函数。

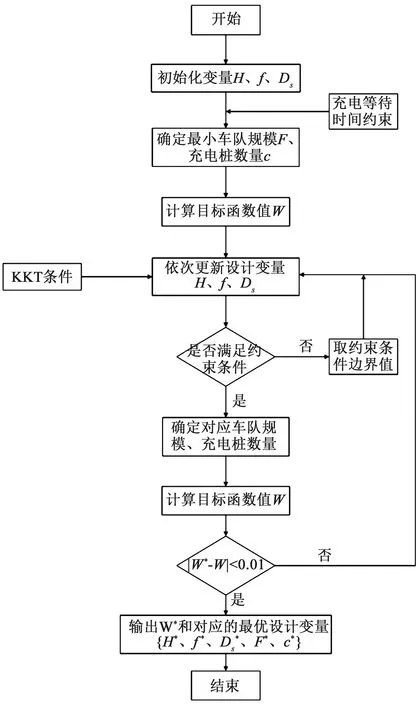
图3 拉格朗日求解算法流程图

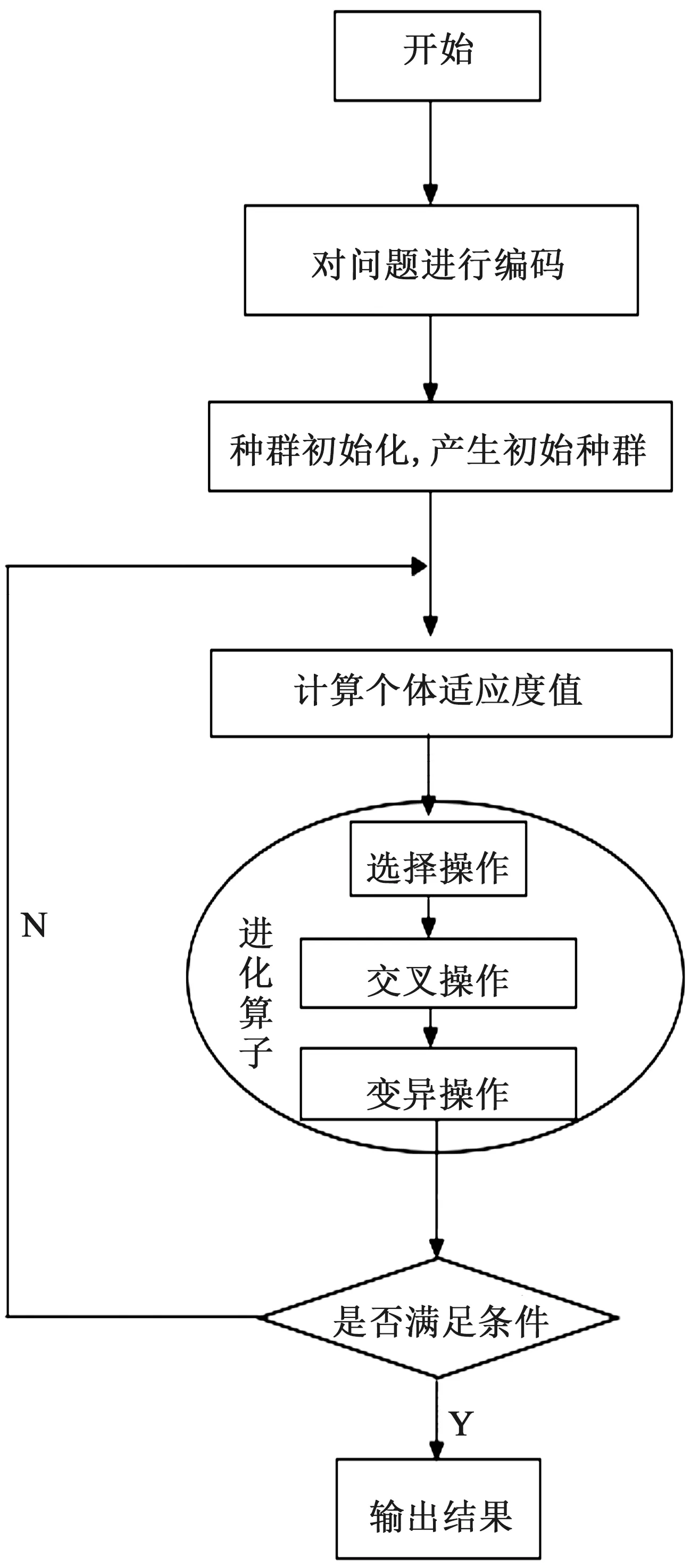
图4 遗传算法流程图

4 算例分析

4.1 算例设置

本节使用一个数值算例来验证文中所提出的模型和求解算法的有效性。以苏州市931路纯电动公交线路为参考案例，如图5所示。

图5 苏州市931公交线路图

苏州市931路公交车服务于新庄立交换乘枢纽和南环桥站之间，公交线路全长约12.4 km，共有23个站点。算例线路长度B设置为12.4 km，人口密度参考苏州市区2016年末平均人口密度1184人/km2，其余参数见表1。

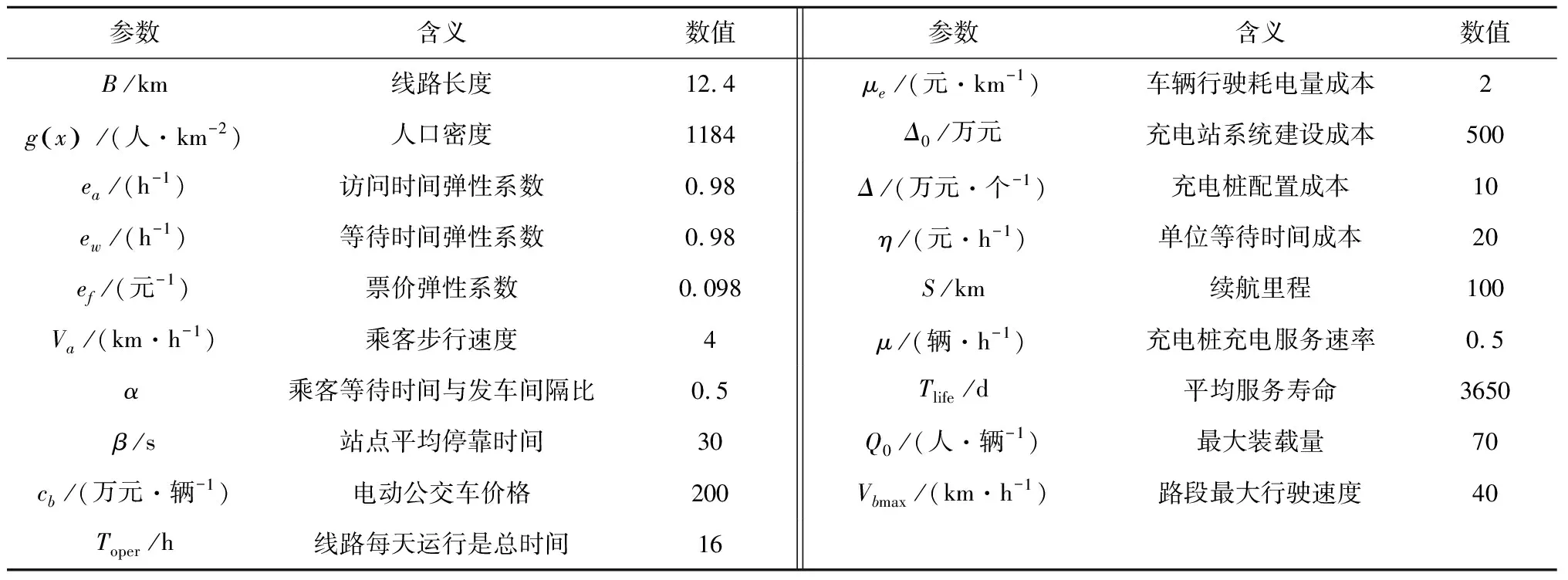
表1 算例参数值

4.2 求解结果分析

4.2.1 基于拉格朗日函数法求解结果

根据第3.1节拉格朗日函数法求解算法对上述算例进行求解。图6表示在不同站点个数情况下的最优福利值，线条表示图中点的拟合曲线。图7表示在不同站点个数情况下，对应求解的最优票价、发车间隔、车队规模和充电桩数量。从图6中可以看出，随着站点的增加，社会福利先增加后减小,其中在第27个站点处社会福利取得最大值，为22 578 元/d。此时票价为0.630 4 元、发车间隔为4.338 9 min、总车队车辆为27辆、充电桩个数为7个。从图7中可以看出，随着站点数增加，车队规模和充电桩个数逐渐增加，而发车间隔逐渐减小，其中车队数量增加速度远大于充电桩数量增加速度。对于票价，根据公式(38)可知其最优值等于运量约束(公式29)的拉格朗日乘子。因此，当最优结果下运力大于运量时，票价则为0，从图7中也可以看出有很多结果为0的情况，如站点数为14、18、20等时，票价为0。相反，当在社会福利最大化模型中运量约束起作用时，票价则不为0。实际中，应避免票价为0的公交线路设计。原因在于如果票价为0，那么将导致出行者或政府出现机会成本的损失[18]。

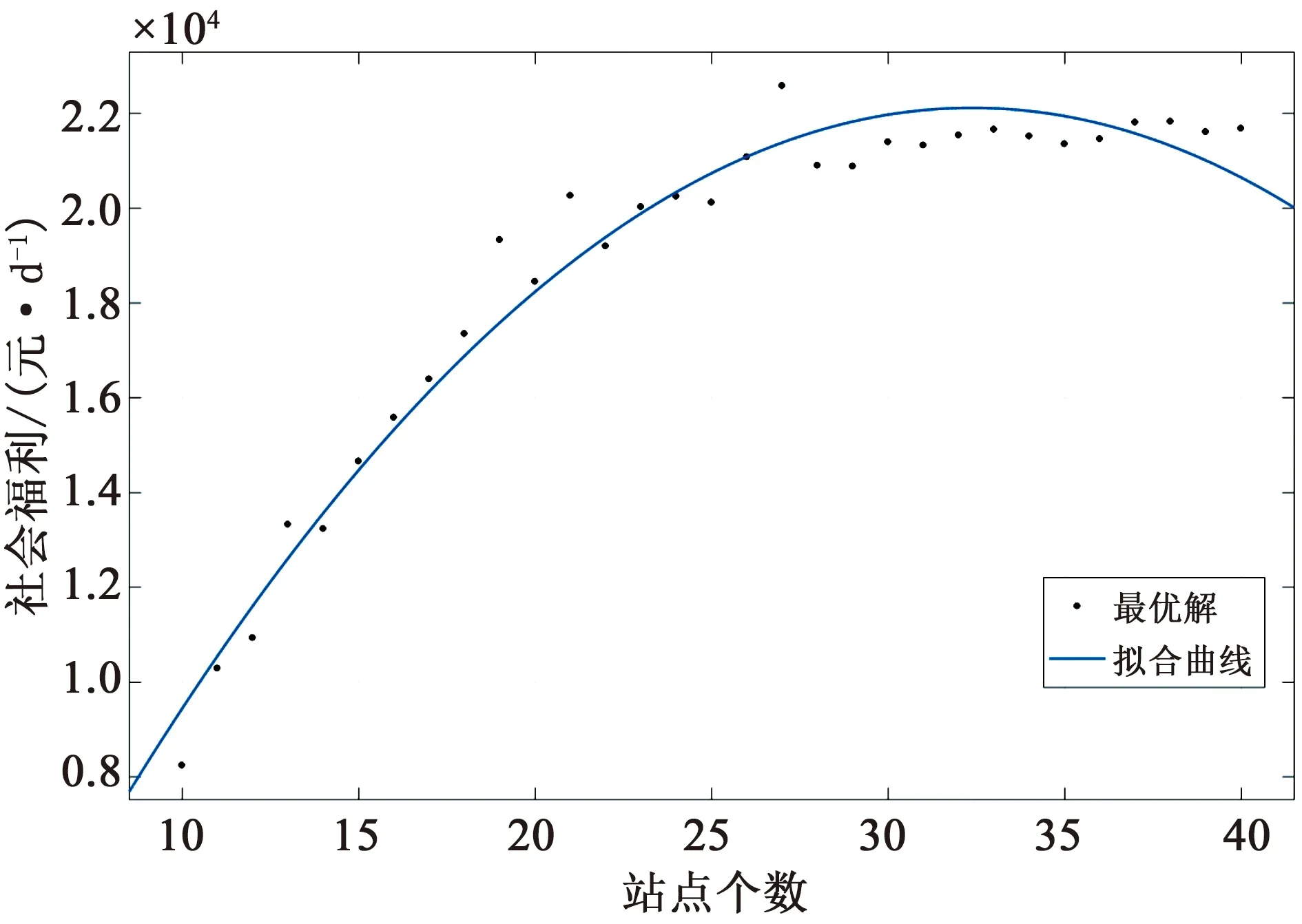
图6 不同站点个数下的最优社会福利

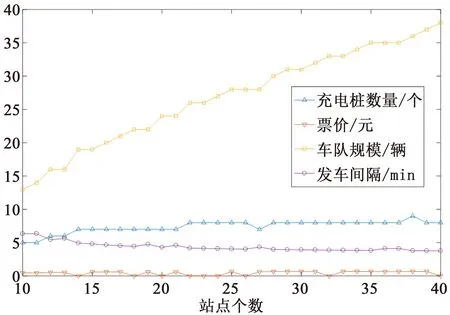
图7 不同站点个数下各变量最优值

4.2.2 遗传算法求解结果

用上述算例中同样的参数，输入遗传算法中，求解结果如图8所示。图8表示每一代种群适应度变化，其中每一代种群最优适应度值的变化即为解的变化。图9是图8中解的变化曲线放大形式，星号点即表示最优解。根据求解结果显示在第31代得到最优结果值，各变量结果分别为票价0.732 4元、发车间隔为4.278 min、车辆数为29辆、充电桩数量为8、站点个数为31个、社会福利值为22 389 元/d。对比两种算法求解结果如表2所示

表2 算法求解结果对比

对比结果显示，拉格朗日函数法求解的最优社会福利值大于遗传算法求解值，且算法运行效率更高(所使用计算机处理器为i7-8550U，内存8 GB)。

图8 遗传算法求解结果图

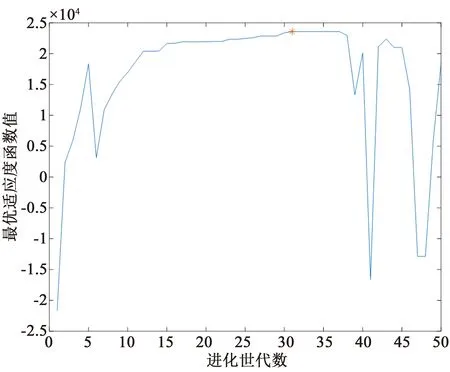
图9 每一代最优个体适应度值

4.3 充电策略对比研究分析

根据社会福利最大化模型(公式28)可知，在票价、发车间隔、站点位置、车队规模、充电桩数量不变情况下，社会福利只与车辆充电等待时间成本有关。以上述算例为例，在站点数为27个、票价为0.630 4元、发车间隔为4.338 9 min、总车队数量为27辆、充电桩个数为7的情况下，根据有限源顾客排队模型(M/M/7/∞/27)得到Ws=2.224 6。

根据情形二分析，将已知变量代入公式(37)得

因此，根据公式(36)可计算出充电站系统中有n辆车排队等待的平稳状态概率pn，表3列出了pn>10-3的值及对应充电系统内车辆数。

表3 主要状态概率值

根据Little公式计算得到L系统=6.896 6，Ws=3.420 9。对比Ws可得到，在此算例中，情形一优于情形二。

情形一和情形二的优劣只取决于车辆充电等待时间成本，而充电等待时间与发车间隔、线路长度、车队规模、充电桩数量有关。由于排队论公式复杂，难以直接化简比较，因此以数值为例，计算两种情形下充电等待时间(充电排队长度)与发车间隔、线路长度、车队规模、充电桩数量之间的关系。

图10a、10b分别表示在发车间隔为10 min、充电桩为7个的情况下，情形一和二中车辆充电排队长度与线路长度和车队规模之间的关系。从图10a中可看出，情形一下，线路长度对排队长度有持续较大影响，而车队规模对排队长度有一定的影响，且随着线路长度变大，影响也变大。而从图10b显示，在情形二下，当车辆数F小于等于c+1时，车队规模对充电桩排队长度影响很大，这是由于充电桩过多，当车辆数低于充电桩数量时，增加车辆数，即是增加充电车辆总数，因此，总的排队长度增加，而当车辆数F大于c+1时，车队规模将对充电桩排队长度影响变的很小。对于线路长度对排队长度的影响，从图10b中可看出，情形二中当线路长度比较短的时候(数值算例中10km以内)，线路长度对排队长度影响大，而当线路过长时，线路长度对于排队长度的影响变低。

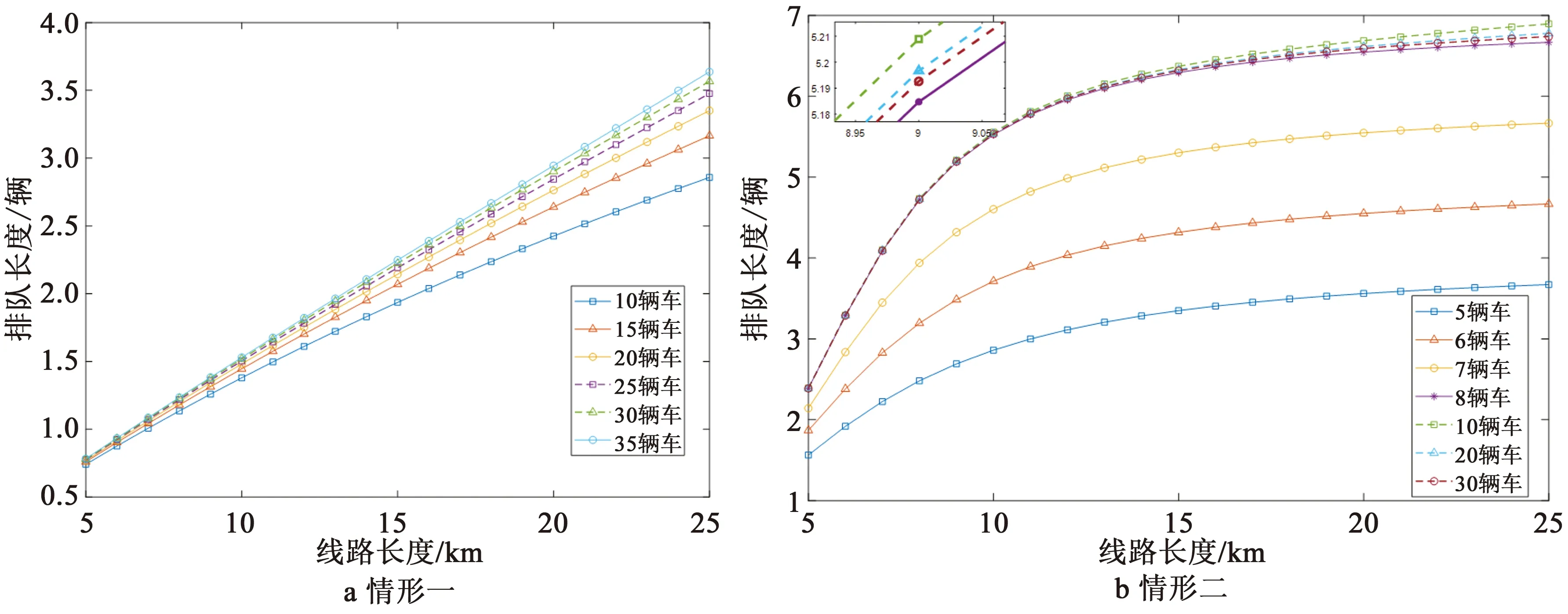
图10 线路长度、车队规模和充电排队长度关系

5 结语

本文以社会福利最大化为目标，建立了线性交通走廊中公交线路设计变量的优化模型。模型考虑电动公交充电等待时间约束，优化了站点数量与位置、发车频率、票价、车队规模以及充电桩数量，以拉格朗日函数法求解算法和遗传算法对模型进行求解，并详细分析了两种不同充电策略对充电排队等待时间的影响，对不同条件下充电策略的优劣进行了比较分析。该模型可为电动公交车线路规划提供决策依据。

依托本文的优化模型，可进一步从以下几个方面进行拓展：(1)往往有多条线路共用一个首末站，因此未来可以进一步研究这个因素对充电桩配置的影响以及电动公交线网规划问题。(2)本文没有考虑人口密度大小对线路参数设计的影响，不同城市人口密度相差很大，而且同一地区随着时间的推移人口密度也会产生较大变化，因此，分析人口密度的影响具有现实意义。(3)车辆规模化生产、充电电池技术进步以及政府补贴政策变化对车辆价格的影响以及车辆运行速度对模型的影响有待进一步研究。