头孢硫脒热分解动力学研究

于帅，程燕，薛富民

(齐鲁工业大学(山东省科学院)山东省分析测试中心，山东 济南 250014)

热分析是一种测量物质物理化学性质的技术，热分析动力学则是一种应用热分析技术研究物质的物理化学性质和化学反应速率及机理的方法[1]。热分析动力学根据分析方法是基于定温还是变温而分为等温动力学(isothermal kinetics)[2]和非等温动力学(non-isothermal kinetics)[3-4]，其中，非等温动力学又包括单升温扫描速率法和多升温扫描速率法。由于多升温扫描速率法具有准确度高等优势，近年来被更多地应用于热力学分析过程中[5-6]。热分析动力学结果是结晶过程中反应器设计和最佳工艺确定的重要评价参数[7]。以Flynn-Wall-Ozawa (FWO)法[8]，Kissinger-Akahira-Sunose (KAS)[9]和 Starink法[10]为代表的多升温扫描速率(multiple-scan method)法, 也是一种等转化率方法(isoconversional method)[11],其特点为不涉及动力学方程的条件下获得较为可靠的活化能Eα，并可以通过比较不同转化率α下的活化能数值来对热分解过程的转化机理的一致性进行核实。近年来，Málek等[12]在总结前人研究的基础上提出了更为完整和完善的热分析动力学测定步骤。

头孢硫脒(cefathiamidine)，CAS号为33075-00-2，化学名称为(6R,7R)-3-[(乙酰氧基)甲基]-7-[α-(N,N-二异丙基脒硫基)乙酰氨基]-8-氧代-5-硫杂-1-氮杂双环[4.2.0]辛-2-烯-2-甲酸内铵盐，中文名为头孢菌素18，又称先锋素18、仙力素[13]。头孢硫脒第一代β-内酰胺类抗生素，对革兰阳性菌、革兰阴性菌、草绿色链球菌等具有较好的抗菌作用，为我国最早自主研发的头孢类抗生素药物，在国内具有广阔的市场空间和应用前景[14]。本文针对头孢硫脒无水物晶体进行了热分析动力学实验与计算，采用多升温扫描速率法中的FWO法、KAS法和Starink法计算得到了热分解活化能Eα，通过Málek法得到了热分解动力学的指前因子A以及对应的动力学模型。并利用以上动力学三因子数据，计算得到了药物的理论贮存期。

1 仪器与材料

1.1 实验仪器

热失重分析(thermogravimetric analysis, TG)使用的为NETZSCH公司的热分析仪(STA449F3)，测试温度为298～373 K，升温速率为分别为5、10、15、20 K/min，N2流速40 mL/min，样品量2～3 mg。样品进样前需放置于干燥器中，采用百万分之一天平进行称量(Mettler Tolerdo, XSR304/AC)，称量结束后立即进样热失重测定。进样选用铝制坩埚，采用标准物质铟进行校准。

1.2 实验材料

2 方法与结果

2.1 数据处理方法

2.1.1 FWO法

Flynn-Wall-Ozawa方法[8, 15]对化合物热分解过程的分析可以通过阿仑尼乌斯方程来推导：

,

(1)

其中r是分解反应速率，α是反应转化率，t为反应时间(s)，A为阿仑尼乌斯指前因子，Eα为反应活化能(kJ/mol)，R为摩尔气体常数取8.314 J/(mol·K)，T为热力学温度(K)，f(α)为反应函数。

对于热分解反应来说，α表示转化率：

(2)

其中m0为样品初始质量(g)，mf为样品最终质量(g)，mα为分解过程中t时刻的质量(g)。

热失重测定过程中升温速率为β：

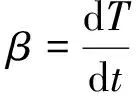
(3)

阿仑尼乌斯方程可以表示为：

(4)

FWO方程可以表示为：

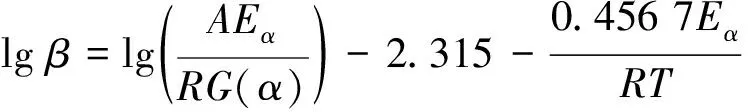
(5)

2.1.2 KAS法

Kissinger-Akahira-Sunose方程[9]可以表示为：

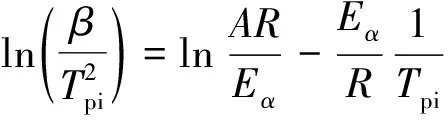
(6)

其中Tpi为相变峰温度(K)。

2.1.3 Starink法

在KAS的基础上，Starink提出了更为精确的Starink方程[10]：

(7)

其中Cconstant为常数项，是Starink方程拟合直线的截距。

2.1.4 Málek法

Málek方法[12]的特点是在不考虑动力学模型的前提下，采用多重扫描速率法求取活化能Eα，然后通过实验数据和两个函数特征值确定动力学模型，该方法避开了逐一尝试动力学方程f(α)的麻烦。Málek方法主要步骤如下：

(1)求取活化能Eα

运用FWO法和KAS法求取活化能并取平均值。

(2)确定动力学模型f(α)

(8)

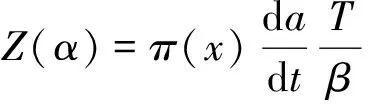
(9)

式中x=Eα/RT，π(x)为Sinum-Yang提出的温度积分近似公式：

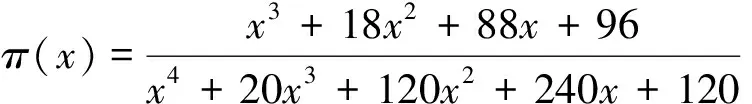
(10)

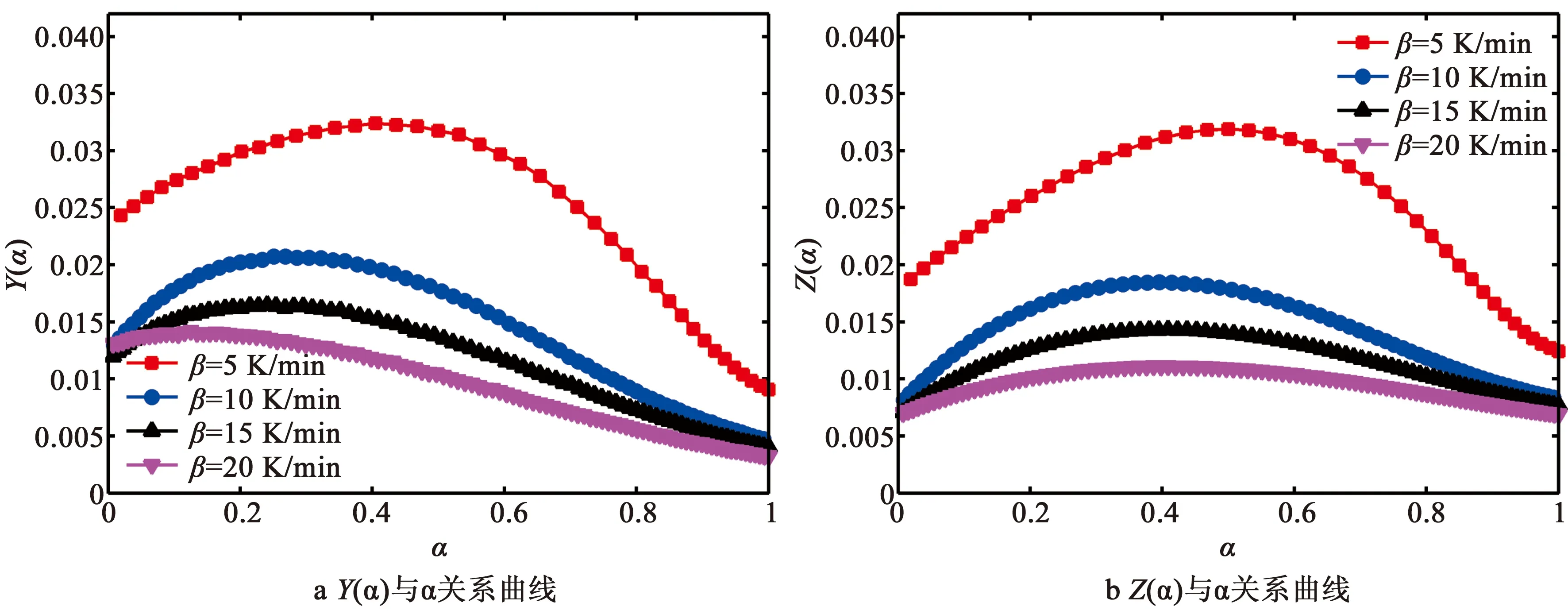
根据Y(α)曲线形状和其极大值处的αm，结合TG-DTG曲线中峰值αp和Z(α)曲线形状和其极大值处的αp∞的值来确定动力学函数模型f(α)，其推理过程如图1所示。

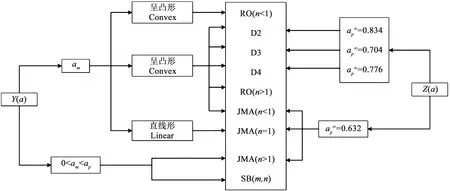
图1 动力学机理判定框图

(3)计算幂指数n和m

根据表1中常见的动力学模型及式(11)～(13)确定动力学幂指数n和m。

ln[(dα/dt)ex]=lnA+nln [αp(1-α)]，

(11)

m=pn，

(12)

p=αm/(1-αm)。

(13)

表1 Málek法对应动力学模型

(4)计算指前因子A

根据已知的活化能和动力学模型，根据方程计算得到指前因子A：

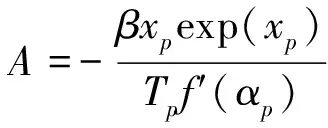
(14)

2.1.5 贮存期计算

根据热分解动力学计算得到的数据和公式[16]，计算在不同温度下的反应速率常数如式(15)所示，由式(16)计算得到药品pk值与药品规定贮存期关系。

(15)

pk=-logk

(16)

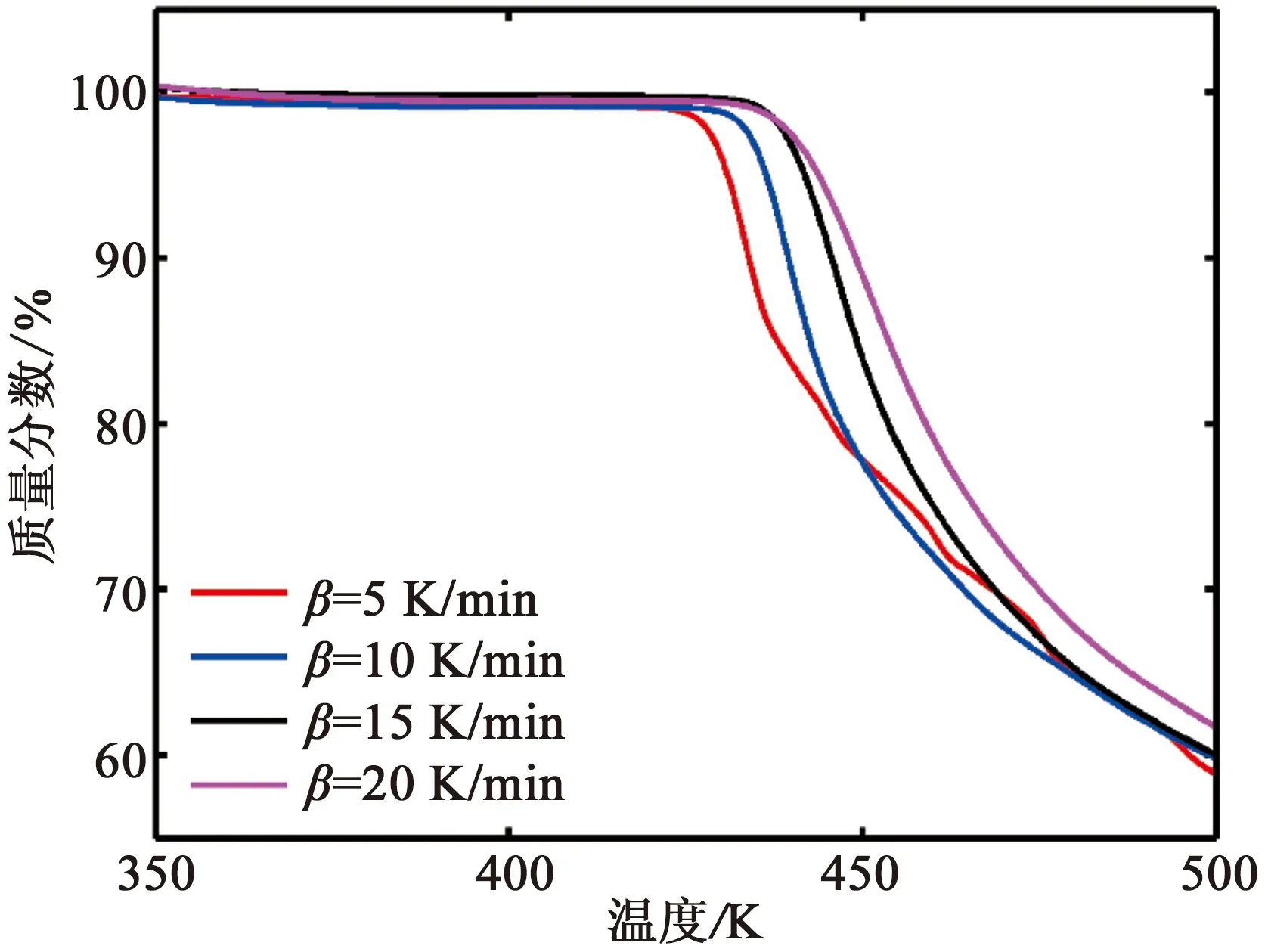
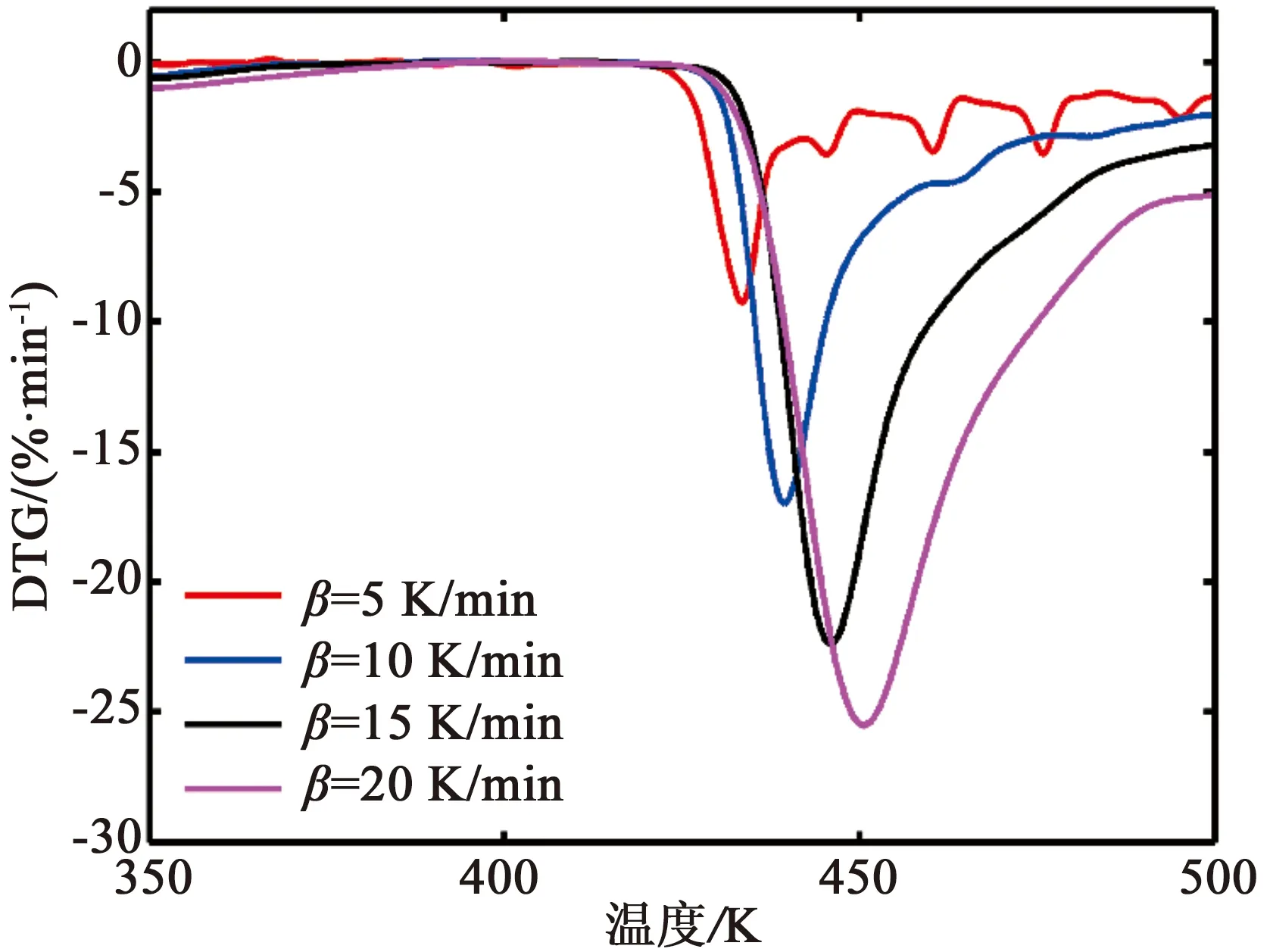
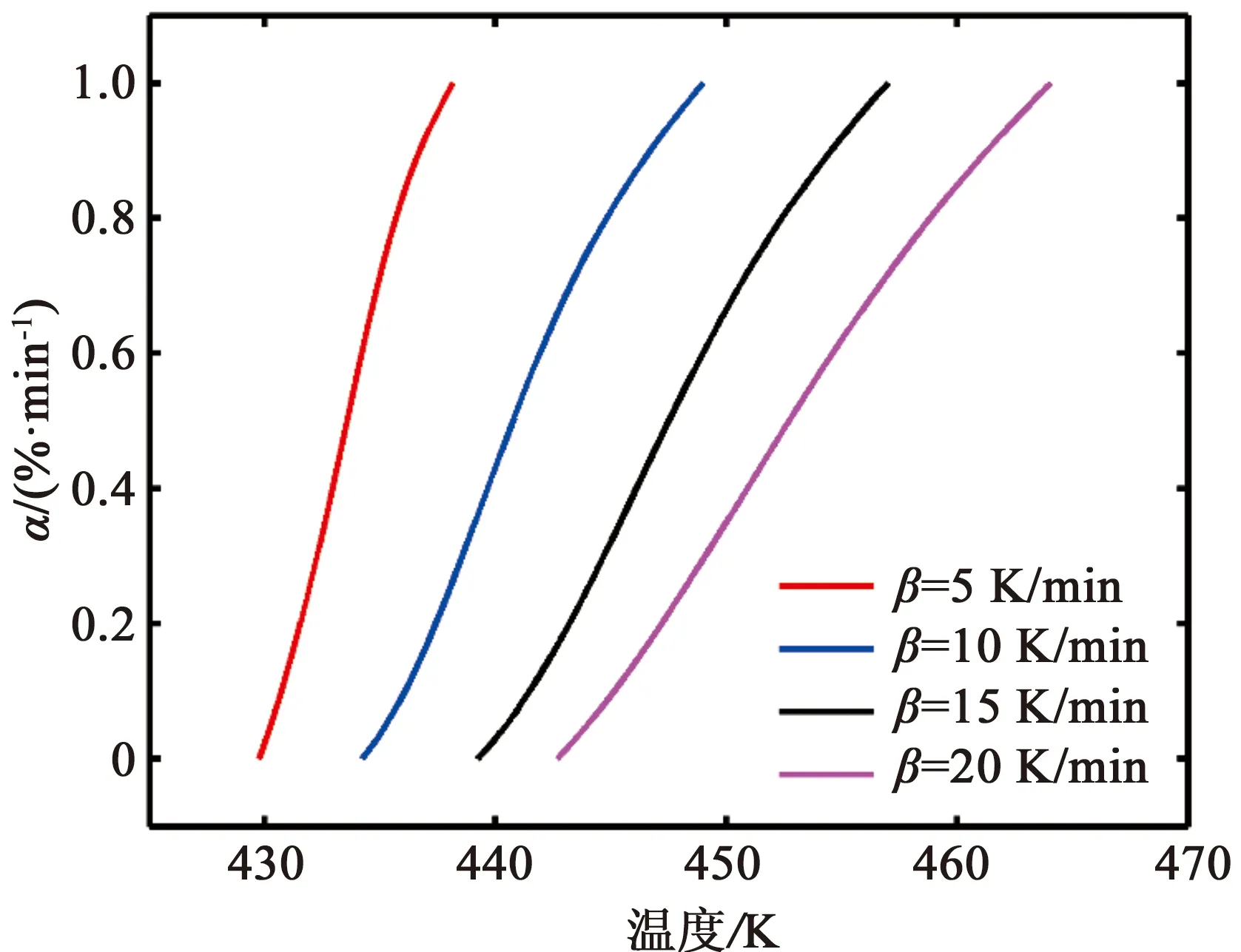
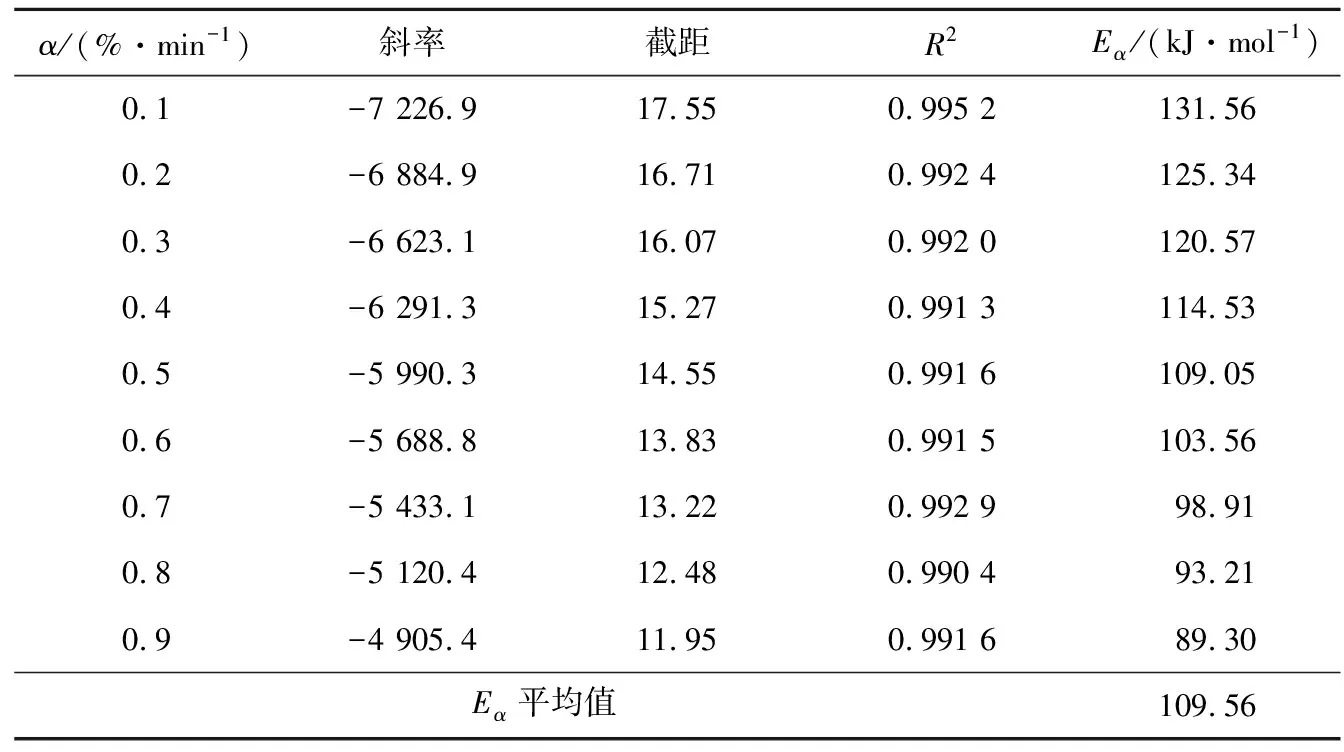
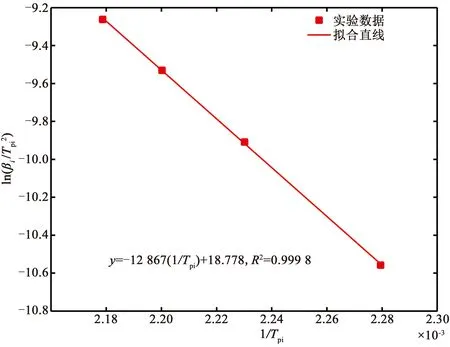
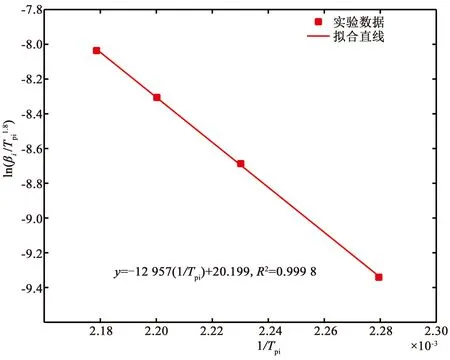
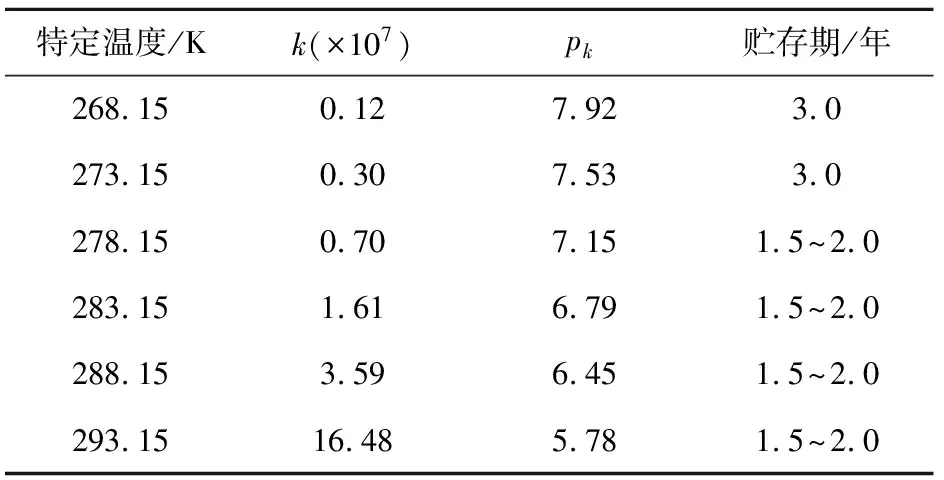
当pk<7.5时，贮存有效期为1.5～2年；当7.5

2.2 结果分析

2.2.1 热重分析

头孢硫脒在升温速率分别为5、10、15、20 K/min时的TG曲线如图2所示，在不同升温速率下热分解速率不同，升温速率越慢，热失重曲线越陡。升到相同的温度时，升温速率快的样品所用的升温时间较少，固体受热相对不均匀，难以完全受热分解，所以热失重台阶会出现拖后的现象。

从DTG曲线(图3，DTG峰值自左到右对应的升温速率逐渐增大)可以看出，曲线在400～500 K只有一个明显的失重峰，说明该温度范围内为同一步失重。一般情况下，热分解动力学都是以第一个明显的热分解峰为研究对象[18-19]。

图2 头孢硫脒热失重曲线

图3 头孢硫脒微分热重曲线

头孢硫脒在不同升温速率下的转化率如图4所示(从左向右对应的升温速率逐渐增大)，当升温速率较快时，晶体的分解温度要高于升温速率较慢时的。较慢的升温速率时，温度上升到一定值时所用的时间较多，晶体的传热更充分，所以在温度较低时就能充分吸热而发生分解。

图4 头孢硫脒热分解过程转化率

2.2.2 FWO法动力学分析

根据FWO方程在相同转化率对应的温度与升温速率的关系，对logβ和1/T作图(图5)，根据直线的斜率进行计算可以得到不同转化率下的活化能值(公式(5))，直线对应的斜率、截距和活化能值如表2所示。随着转化率的增大，热分解活化能逐渐减小，其平均值为109.56 kJ/mol，与转化率为0.5时的活化能数值(109.05 kJ/mol)接近。

图5 头孢硫脒热分解过程不同转化率时log β对1/T线性回归图

表2 头孢硫脒不同转化率时计算得到的热分解动力学回归参数及活化能(FWO法)

2.2.3 KAS法动力学分析

表3 头孢硫脒不同升温速率对应热分解温度

图6 KAS方程计算活化能拟合曲线

根据KAS方法计算得到的不同升温速率对应的热分解峰的峰值如表3所示，随着TG升温速率的增大，热分解峰值的温度逐渐增大。图6为ln (β/Tpi2)对1/Tpi作图的拟合直线，拟合方程为y=-12867x+18.788，R2=0.999 8。由直线的斜率可以计算得到热分解活化能(式6)，计算得到的平均活化能为106.96 kJ/mol。

2.2.4 Starink法动力学分析

图7为ln(β/Tpi1.8)对1/Tpi作图的拟合直线，由直线的斜率可以计算得到热分解活化能(式7)。根据Starink方法计算得到的平均活化能为107.70 kJ/mol。

图7 Starink方程计算活化能拟合曲线

2.2.5 Málek法动力学分析

通过多项式对Y(α)-α(图8a)和Z(α)-α(图8b)进行拟合，对拟合方程求导可以得到不同升温速率下的αm和αp∞(表4)，根据动力学机理判断框图(图1)和特征参数值，可以判断动力学模型为SB(m,n)。计算得到的参数值m=0.241 7，n=0.658 9，根据Málek方法计算得到的Eα=109 kJ/mol，lnA=30.60 s-1，动力学模型为SB(0.241 7, 0.658 9)。

图8 Y(α)、Z(α)与α关系曲线

表4 头孢硫脒Y(α)-α和Z(α)-α函数特征参数

2.2.6 贮存期分析

特定温度下的贮存期如表5所示(式16)，说明头孢硫脒药物在273.15 K以下时贮存期可以达到3年以上，应当在低温下进行保存。

表5 头孢硫脒特定温度下反应速率常数与理论贮存期

3 结论

(1)通过TG多升温速率法测定了头孢硫脒的热分解过程。通过FWO法、KAS法和Starink法计算了头孢硫脒热分解过程中的活化能值，发现活化能均随着热分解转化率的升高而降低，且FWO法计算值(109.05 kJ/mol)>Starink法计算值(107.70 kJ/mol)>KAS法计算值(106.96 kJ/mol)。

(2)通过Málek方法计算得到了热分解动力学指前因子和热分解动力学模型，头孢硫脒晶体的热分解动力学三因子分别为Eα=109 kJ/mol，lnA=30.60 s-1，动力学模型SB(0.2417, 0.658 9)；

(3)计算了理论贮存期，头孢硫脒在273.15 K以下时理论贮存期为3年，头孢硫脒药物在室温下稳定性较差，需要冷藏储存。