运算能力的培养在争辩与迁移中生长
张靖
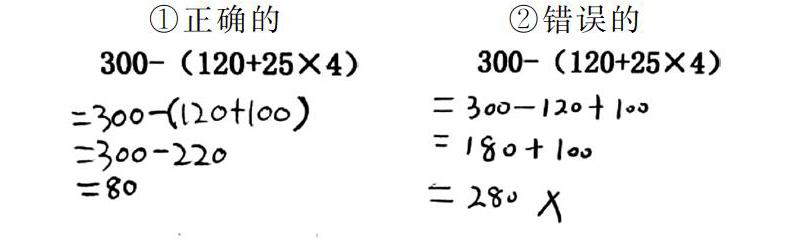
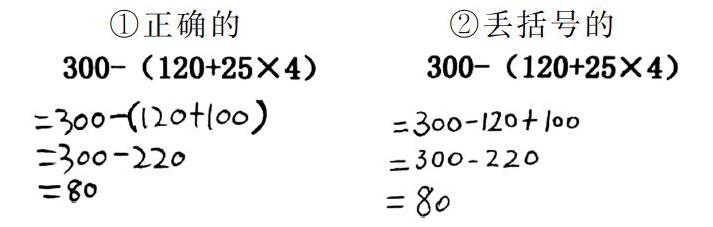

摘 要:运算能力是数学的核心概念之一,对于小学阶段的学习,运算能力的培养至关重要,直接影响学生的数学学习能力,小学阶段的计算课显得尤为重要。从教材的编排来看,计算类型的课呈块状有层次地出现并符合学生的年龄特点。对于教师来说,计算课不是枯燥无味地教计算,而是悟算理和教算法有机结合,为了使计算课更有数学味,本文提出以下三点建议:一、有层次呈现错误资源,使学生从错误中总结运算规律;二、对于新题型给学生思考的空间,让学生在争辩中总结新的运算技巧;三、通过知识的迁移,观察新旧知识之间的联系,找到共同点,进而总结算法,掌握算理。
关键词:运算能力;错误资源;争辩;迁移
“错误资源”显真知,学生评价察算理
《含有小括号的三步混合运算》是在已经教学了《不含小括号的三步混合运算》的基础上进行学习的,学生已经有了一定的计算基础,对于运算顺序的掌握也相当到位,但是对于括号的处理却仍处于未知或疑惑状态。对此,教师通过展示不同的作业资源并交由学生评价,是引导学生判断括号在混合运算中的使用方法以及括号对于运算顺序的影响,学生通过对不同资源的处理有效解决对含有括号的三步混合运算的疑惑。
[教学片断1]
计算300-(120+25×4),明确运算顺序
(1) 师:那我们先来试一试,先想一想运算顺序再下笔。
(2) 交流:
预设呈现一:
①正确的
②错误的
师:一起来看一看,2种做法得数不同,哪一种是正确的。
生:第一种正确。
师:谁来说说他是怎么算的?
生:先算乘法、再算加法、最后算减法。
师:那第二种做法你同意吗?问题出在哪了?
生:第二份是先算乘,再算减,最后算加。
师:是啊,运算顺序发生了错误,所以得数也错了。(在学生作业纸上打叉)
预设呈现二:
①正确的
②丢括号的
师:这份作业确实是先算小括号里的乘,再算加,最后算减,他这样写大家同意吗?
生:不同意,因为括号丢了,应该先算乘再算减最后算加。
师:是啊,括号里没有算完,小括号要保留不能丢。
预设呈现三:
①正确的
②跳步骤计算的
师:诶,这份作业你看得懂吗,谁来说说?
生:他跳步驟了,括号里两步一起算了。
师:的确是这样的,那你觉得跳步骤好不好呢?
学生争辩。
师:为了提高正确率,建议大家还是按照运算顺序一步一步进行计算。
上述环节,用了四份作业,三次对比,使学生内化算法,掌握算理。三个层次的对比都有其存在的道理,第一次对比,使学生感受到运算顺序对混合运算的影响,如果运算顺序发生了错误,那么得数也就错了;第二次对比,使学生意识到小括号的作用,如果括号里没有算完,小括号不能丢,否则会改变运算顺序;第三次对比,通过争辩得出两种方法都可以,为了提高正确率,也为了刚开始保持良好的计算习惯,建议学生按照运算顺序一步一步往下算。通过三个层次的交流,让学生的计算学习更加靠近教学目标的定位,从常见的错误中感悟运算顺序和小括号对混合运算的重要性。这样的学习过程,才是计算知识的生长过程,更符合小学阶段学生的认知需要。
[教学片断2]
计算四道题,看谁做得又快又好。
25×(22+576÷32) 6×58-(74+89) 540÷(30×15÷50) 120×(10-10÷5)作业交流
层次一:(先呈现全对)
练习三:先想一想运算顺序,再计算。
师:刚刚大家都说小括号不要丢,第一题括号没丢,第三题没丢,第四题没丢。咦?第2题的小括号怎么丢了呢?(红笔描出括号)
生:因为第1、3、4道的小括号里是两步计算,第2题小括号里只有一步计算。
师:那就奇怪了,小括号什么时候可以保留,什么时候可以去掉?
生:小括号里算完了括号可以去掉,没算完括号要保留。
层次二:
师:最后一题还有个同学是这样做的。错在哪?
生:运算顺序不对,应该先算除法,再算减法。
师:(对比第一题)为什么这里他还知道先算加再算除,到了这儿这么忘了呢?
生:数字比较简单。
师:是啊,10-10=0太简单了,他被数字迷惑了,可见我们不能被数字干扰,想清楚运算顺序再下笔。
层次三:
师:老师还发现这道题有2种做法,得数都是185,你有什么想说的?
学生争辩。
师小结:因为乘法是高级运算,加法加上括号就升级了,中间却是低级运算,所以两边同时先算,这不违反运算顺序,也是可以的,所以这两份作业都是正确的。
上述环节,用了三份作业,通过三个层次的交流,帮助学生解决了含有小括号的三步混合运算中的一些易错点。层次一:教师通过四道题的对比,帮助孩子解决括号什么时候去掉,什么时候保留的问题,孩子通过例题的对比发现,括号里算完了括号就可以去掉,学生通过探究发现规定背后的道理,这比教师直接告知来得更加有效;层次二:教师通过一道错题引发孩子们的思考,为什么在熟记了运算顺序的情况下仍然会算错?学生通过不同题目的对比发现,当数字比较简单的情况下,会被简单的数字干扰导致算错,通过错题提醒学生计算前还是要细致观察运算顺序,这比教师耳提面命地提醒学生细心计算来得更为直观有效;层次三:教师通过两种不同的做法引起学生争论,在我们计算时能否有不同的计算思路?通过生生交流与争论,得出两种做法都可以的结论,学生的观点被赞同比教师强行灌输来得更有说服力。

